
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ХАРЧОВИХ ТЕХНОЛОГІЙ
ВИЩА МАТЕМАТИКА
МЕТОДИЧНІ РЕКОМЕНДАЦІЇ до виконання розрахунково-графічних робіт
для студентів напрямів підготовки 6.051701 “Харчові технології та інженерія “, 6.040106 “Екологія, охорона навколишнього середовища та збалансоване природокористування “, 6.051301 “Хімічна технологія “, 6.051401 “Біотехнологія “ денної форми навчання
Київ НУХТ 2013
Вища математика. Метод. рекомендації до виконання розрахунковографічних робіт для студентів напрямів підготовки6.051701 “Харчові технології та інженерія “, 6.040106 “Екологія, охорона навколишнього середовища та збалансоване природокористування “, 6.051301 “Хімічна технологія “, 6.051401 “Біотехнологія “ денної форми навчання / Укл.: О.П. Зінькевич, В.М. Сафонов, О.В. Островська, С.І. Резніков, В.М. Романенко, К.М. Сологуб, В.П. Шоха, Г.А. Циганкова – К.: НУХТ, 2013. – 91 с.
Рецензент А.С. Богатирчук, кандидат фіз.-мат. наук.
Укладачі: О.П. Зінькевич,
В.М. Сафонов, О.В. Островська, С.І. Резніков,
В.М. Романенко, кандидати фіз.-мат. наук,
К.М. Сологуб, Г.А. Циганкова, В.П. Шоха.
Відповідальний за випуск М.А.Мартиненко, д-р фіз.-мат. наук, проф.
Видання подається в авторській редакції
2
Мета методичних рекомендацій – допомогти студентам денної форми навчання опанувати курс вищої математики.
У запропонованих методичних рекомендаціях викладені загальні рекоме - ндації щодо виконання розрахунково-графічних робіт, основні означення, формули, розв’язання типових задач, список рекомендованої літератури та задачі для розрахунково-графічних робіт.
І. Вступ.
Розрахунково-графічна робота – важлива форма самостійної роботи студента.
У процесі вивчення курсу вищої математики студенти повинні виконувати розрахунково-графічні роботи, кількість яких та розділи матеріалу встановлюються навчальними планами та програмами.
Розпочинати виконання розрахунково-графічної роботи слід лише після вивчення відповідних розділів курсу і розв’язання достатньої кількості задач, при цьому студенту рекомендується дати відповіді на запитання, наведених після кожної теми в даних методичних рекомендаціях.
Номери розрахунково-графічних робіт та задач наведені в останньому розділі запропонованих рекомендацій.
Під час виконання розрахунково-графічної роботи студент повинен -до тримуватися таких вимог:
1)Розрахунково-графічну роботу студент повинен виконувати за своїм варіантом.
2)Кожну розрахунково-графічну роботу треба виконувати в окремому
зошиті.
3)Робота, виконана ( повністю або частково ) за чужим варіантом,
не зараховується.
4) Перед розв’язанням кожної задачі слід повністю переписати її умову, замінивши загальні дані конкретними зі свого варіанту. Розміщувати задачі ( та їх розв’язування) в порядку зростання номера, зберігаючи нумерацію; розв’язування задач записувати акуратно, розбірливо, супроводжуючи відповідними рисунками.
5) Кожну виконану розрахунково-графічну роботу захистити до початку екзаменаційної сесії.
6) Студент, який не виконав або не захистив хоча б одну розрахунковографічну роботу, до екзамену (заліку) не допускається.
3

ІІ. Методичні рекомендації до розв’язання завдань розрахунково-графічних робіт.
1. Елементи лінійної алгебри [1, c. 6 - 12, 20 - 23], [2, c. 3 - 9].
Вирази D |
a11 |
a12 |
a11 × a22 - a12 × a21 , |
|
|
|
|
|
|
|
|
|||
= |
= |
|
|
|
|
|
|
|
|
|||||
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
D |
a= |
a= |
a |
a |
× a |
× a |
+ a |
× a |
× a |
+ a |
× a |
23 |
× a |
- |
|
21 |
22 |
23 |
11 |
22 |
33 |
21 |
32 |
13 |
12 |
|
31 |
|
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
-a13 × a22 × a31 - a12 × a21 × a33 - a23 × a32 × a11
називаються відповідно, визначниками другого і третього порядків. Символами aij позначаються елементи визначника, причому перший ін-
декс i показує номер рядка, а другий індекс j – номер стовпця, на перетині яких стоїть даний елемент.
1.1. Розв’язання систем лінійних рівнянь за формулами Крамера.
Нехай задано систему трьох лінійних рівнянь з трьома невідомими x, y, z :
ìa x + a y + a z = b ; |
|
|||
ï 11 |
12 |
13 |
1 |
(1) |
ía21x + a22 y + a23 z = b2 ; |
||||
ïa x + a y + a z = b . |
|
|||
î 31 |
32 |
33 |
3 |
|
Де aij (i = 1,3, j = 1,3) - коефіцієнти при невідомих, bi (i =1,3) - вільні члени.
Обчислимо визначники:
|
a11 |
a12 |
a13 |
|
|
|
|
b1 |
a12 |
a13 |
|
|
|
D = |
a21 |
a22 |
a23 |
; |
Dx = |
b2 |
a22 |
a23 |
|
; |
|||
|
a31 |
a32 |
a33 |
|
|
|
|
b3 |
a32 |
a33 |
|
|
|
|
|
a11 |
b1 |
a13 |
|
|
|
a11 |
a12 |
b1 |
|
|
|
|
|
|
|
|
|||||||||
Dy = |
a21 |
b2 |
a23 |
|
; |
Dz = |
a21 |
a22 |
b2 |
|
, |
||
|
|
a31 |
b3 |
a33 |
|
|
|
a31 |
a32 |
b3 |
|
|
|
де D – визначник системи, складений з коефіцієнтів aij системи (1). Ви-
значники Dx , Dy та Dz утворюються із визначника D відповідно заміною стовп-
ців при невідомих x, y та z стовбцем вільних членів b1, b2 , b3. Можливі такі випадки (теорема Крамера):
1) D ¹ 0. Тоді система (1) має єдиний розв’язок (визначена), який знаходиться за формулами Крамера:
x = |
Dx |
, |
y = |
Dy |
, |
z = |
Dz |
. |
|
|
|
||||||
|
D |
|
D |
|
D |
|||
4

2) D = 0 , та Dx ¹ 0 або D y ¹ 0 , або Dz ¹ 0 , тобто хоча б одне з чисел
Dx , Dy , Dz не дорівнює нулю, то система (1) розв’язку не має (несумісна).
3)D = Dx= Dy= Dz= 0. Тоді система (1) може бути несумісною або мати безліч розв’язків (невизначеною).
Приклад. Розв’язати систему рівнянь:
ì2x + 3y - z = 5
ï |
5y - 2z = 2 |
í |
ïî4x + y + 8z = 0
Розв’язання. Обчислимо визначник системи:
2 3 -1
D =0 5 -2 = 80 - 0 - 24 + 20 + 4 - 0 = 80 . |
||||||||||||||||
4 |
|
1 |
8 |
|
|
|
|
|||||||||
D ¹ 0 , отже, система має єдиний розв’язок (визначена). |
||||||||||||||||
|
|
5 |
|
|
3 |
|
-1 |
|
|
|
|
|||||
|
|
|
||||||||||||||
Dx = |
|
2 |
|
|
5 |
- 2 |
|
= 200 - 2 + 0 + 0 +10 - 48 =160, |
||||||||
|
|
0 |
|
|
1 |
|
8 |
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
5 |
-1 |
|
|
|||||||
|
|
|
||||||||||||||
D y = |
|
0 |
2 - 2 |
|
= 32 - 0 - 40 + 8 + 0 + 0 = 0, |
|||||||||||
|
|
|
|
4 |
|
0 |
8 |
|
|
|||||||
|
|
2 |
|
|
3 |
5 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
Dz = |
|
0 |
|
|
5 |
2 |
|
= 0 + 0 + 24 -100 - 0 - 4 = -80. |
||||||||
|
|
4 |
|
|
1 |
0 |
|
|
|
|
|
|
||||
За формулами Крамера маємо:
|
D |
x |
160 |
|
|
Dy |
0 |
D |
z |
-80 |
|
|||
x = |
|
= |
|
= 2; |
= =y |
= |
= |
0;= = z |
|
|
|
-1. |
||
D |
|
D |
80 |
|||||||||||
|
80 |
|
|
D |
80 |
|
||||||||
Запитання до самоконтролю
1.Сформулюйте означення визначника.
2.Що називається системами лінійних алгебраїчних рівнянь?
3.Яка система лінійних рівнянь називається сумісною, несумісною, визначеною, невизначеною?
4.Запишіть формули Крамера. Коли застосовуються формули Крамера?
2.Елементи векторної алгебри [1, c. 32 - 65], [2, c.10 - 25].
2.1.Поняття вектора.
Задамо на довільній прямій дві точки А і В. Будемо вважати А початковою точкою, а В– кінцевою. Напрямлений відрізок АВ прямої називається вектором,
®®
який позначається символом AB або а . Модулем (довжиною) вектора назива-
5

® ®
ється відстань між його початком та кінцем, який позначається | AB | або | а | . Вектори називаються колінеарними, якщо вони лежать на паралельних прямих. Вектори, що лежать на одній або на паралельних площинах, назива-
ються компланарними.
Нехай задано координати точок A(xА ; yА ; z А ) і B(xВ ; yВ ; zВ ), то координати
|
® |
|
|
|
® |
|
|
|
|
вектора AB обчислюються так: |
AB = (xB - xA ; yB - yA ; zB - zA ). Якщо позначити |
||||||||
|
|
|
|
|
® |
|
(ax ;ay ;az ). |
||
|
через ax = xB - xA , ay = yB |
- yA , az = zB - zA , то AB = |
|||||||
|
Вектор можна записати також у вигляді розкладу за базисними векторами |
||||||||
® ® ® |
® |
® |
® |
® |
|
|
|
|
|
i , j, k , а саме AB = ax |
i + ay |
j+ az |
k . |
|
|
|
|||
|
Довжина вектора обчислюється за формулою: |
|
|
|
|||||
|
® |
|
|
|
|
|
|
|
|
|
|
(xВ - xА )2 + y( В - yА )2 + z(В - z А )2 = ax 2 + ay2 + az2 . |
|||||||
|
| AB | = |
|
|||||||
|
® |
|
|
|
|
|
|
|
|
Нехай вектор a = (ax ; ay ; az ) утворює з осями декартової прямокутної системи координат Ох, Оy і Оz відповідно кути a , b і g . Косинуси цих
кутів називають напрямними косинусами вектора і визначають за формулами:
|
a |
ay |
a |
® |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
cosa = |
x |
, cos b = |
|
, cosg = |
z |
, де | a |= |
ax + ay2 + az2 . |
||
® |
® |
® |
|||||||
| a | |
| a | |
| a | |
|
|
|
||||
Сума квадратів напрямних косинусів дорівнює одиниці: cos2 a + cos2 b + cos2 g = 1.
2.2. Скалярний добуток векторів.
Скалярним добутком двох векторів називається число, яке дорівнює добутку модулів цих векторів на косинус кута між ними.
|
|
® ® |
|
|
|
® ® |
|
|
|
|
|
|
|
Скалярний добуток двох векторів а і b позначається: а× b і обчислюється |
|||||||||||||
|
® ® ® |
® |
|
|
|
|
|
|
|
|
|
|
|
за формулою: а× b = | а || b | cosj , де j – кут між векторами. |
|
|
|
|
|
) |
|
||||||
Якщо |
відомі |
® |
і |
® |
, |
тобто |
® |
;a |
|
;a |
|
і |
|
координати векторів |
b |
a = (a |
y |
z |
|||||||||
|
|
а |
|
|
|
x |
|
|
|
|
|||
® |
), то має місце формула: |
|
|
|
|
|
|
|
|
|
|
|
|
b = (bx ;by ;bz |
|
|
|
|
|
|
|
|
|
|
|
||
® ®
а× b = = ax bx + ay by + azbz .
® ® ® ®
Виходячи із рівностей а× b = | а || b | cosj = ax bx + ay by + az bz , маємо для ку-
та між векторами співвідношення:
|
cosj = |
|
|
ax bx + ay by + az bz |
|
. |
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
a2 |
+ a2 |
+ a2 |
b2 + b2 |
+ b2 |
|||
|
|
|
x |
y |
z |
x |
y |
z |
||
|
|
|
|
|
|
|
|
|
® ® |
|
Умова перпендикулярності двох ненульових векторів а і b : |
||||||||||
® ® |
® ® |
|
|
|
|
|
|
® ® ® ® |
||
а ^ b тодіі тільки тоді, якщо а× b = axbx |
+ ay by |
+ az bz |
= 0 , при цьому a ¹ 0 , b ¹ 0 . |
|||||||
6
Розглянемо задачу про обчислення роботи. Нехай матеріальна точка переміщується прямолінійно із положення M в положення N під дією сталої сили
® ® ®
F , яка утворює кут j із переміщенням MN = L . Тоді робота A обчислюється
®®
за відомою формулою: A = | F || L | cosj .
Математична сутність цієї формули в тому, що двом векторним величинам
®®
F і L поставлена у відповідність скалярна величинаA . Ця підстава послужила причиною для введення математичної дії множення векторів, результатом виконан-
®®
ня якої є скаляр. Отже A = F× L .
2.3. Векторний добуток векторів.
® |
® |
® |
Векторним добутком вектора а |
на вектор b |
називається вектор с , |
®®
який позначається а´ b , і має такі властивості :
® ® ®
1) модуль с дорівнює добутку модулів векторів а та b на синус кута між
®® ® ® ®
ними, тобто | с |=| а´ b |= | а || b | sin j ;
® |
® ® |
2) вектор с перпендикулярний до кожного з векторів а і b ; |
|
® |
направлений таким чином, що найкоротший поворот від |
3) вектор с ¹ 0 |
|
®®
адо b видно з його кінця проти руху годинникової стрілки.
®®
Модуль векторного добутку векторів а і b дорівнює площі S паралелог-
®®
рама, побудованого на векторах а і b , віднесених до спільного початку:
® ® ® ® |
|
æ |
® Ù ® |
ö |
|
|
|
|
1 |
|
® ® |
|
|
|
|
|
|
|
||||||||
S пар =| а´ b |= | а || b | sin j, j = ç |
а, |
b |
÷ |
; SD |
= |
|
|
| а´ b | – площа трикутника. |
||||||||||||||||||
2 |
||||||||||||||||||||||||||
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
® ® ® |
|||||||
Векторний добуток двох колінеарних векторів є нуль-вектор: а´ b = 0 , то- |
||||||||||||||||||||||||||
|
® |
® |
|
|
|
|
® |
|
® |
|
® |
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
|
ді і тільки тоді, якщо а b , причому a ¹ 0 , |
b ¹ 0 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
® |
® |
® |
® |
® |
|
|
® |
|
|
® |
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
||
Якщо a = ax |
i + ay |
j+ az k , b = bx |
i + by |
j+ bz k , то |
|
|
|
|
|
|||||||||||||||||
|
|
® |
® |
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а´ b = |
i |
j |
k |
|
= i |
|
ay |
|
az |
|
- j |
|
ax |
az |
|
+ k |
|
ax |
ay |
|
. |
|||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
ax |
ay |
az |
|
|
|
|
|
|
|
|
||||||||||||||||
® ® |
|
|
|
|
|
® |
|
|
|
|
|
|
® |
|
|
|
|
|
® |
|
|
|
|
|
||
|
|
bx |
by |
bz |
|
|
|
|
by |
|
bz |
|
|
|
|
bx |
bz |
|
|
|
bx |
by |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2.4.Мішаний добуток векторів.
®® ®
Нехай задано три вектора а , b , с . Множення яких можна виконати різ-
|
|
æ |
® |
® ö |
® |
æ |
® ® ö |
® |
ними способами. Зокрема, можна утворити такі добутки: ça´ b ÷ |
× c |
, ça× b ÷ |
× c , |
|||||
|
|
è |
|
ø |
|
è |
ø |
|
æ® |
® ö |
® |
|
|
|
|
|
|
також ça´ b ÷ |
´ c . |
|
|
|
|
|
|
|
è |
ø |
|
|
|
|
|
|
|
7
|
Перший з добутків |
æ® |
® ö |
® |
|
|
|
|
|
|
|
|
|
® |
® |
||
|
ça´ b ÷ |
× c − це скалярний добуток вектора а´ b на вектор |
|||||||||||||||
|
|
|
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
® |
|
|
|
|
|
|
|
|
|
® |
® ® |
|
|
® ® ® |
|||
с . Він називається мішаним добутком векторів а , b , с і позначається а b с . |
|||||||||||||||||
|
Геометричний зміст мішаного добутку: |
|
|
|
|
|
|
|
® |
||||||||
|
модуль мішаного добутку векторів а , |
||||||||||||||||
® |
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
® |
® |
® |
b , |
с дорівнює об’єму паралелепіпеда, побудованого на векторах а , b і с , віднесених |
||||||||||||||||
|
|
|
|
® ® ® |
|
|
|
® ® ® |
|
|
|
|
|
||||
до спільного початку: V |
|
= | а b с | або V |
|
= |
1 |
| а b с | – об’єм трикутної піраміди. |
|||||||||||
|
пір |
|
|||||||||||||||
|
|
пар |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
® |
® |
® |
® ® |
® |
|
® |
|
® ® |
® |
® |
® |
|||||
|
Якщо a = ax |
i + ay |
|
j+ az |
k , b = bx |
i + by |
j+ bz |
k , с = сx |
i + сy |
j+ сz |
k , то |
||||||
|
|
|
|
|
|
® ® ® |
|
|
ax |
|
ay |
az |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
bx |
|
by |
bz |
|
|
|
|
|
|
|
|
|
|
|
|
а b с = |
|
|
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
сx |
|
сy |
сz |
|
|
|
|
|
Мішаний добуток векторів дорівнює нулю тоді і тільки ,тодіколи якийнебудь із векторів – нульовий або коли вектори компланарні (тобто лежать на одній площині або на паралельних площинах).
|
|
|
® ® ® |
|
З формули випливає умова компланарності векторів а , b і с : |
||||
|
ax |
ay |
az |
|
|
bx |
by |
bz |
= 0. |
|
сx |
сy |
сz |
|
Приклад. Дано точки A(3;-2; 0), B(1;2;-4), C(1;0;1), D(1;5; 2). Зобразити у декартовій прямокутній системі координат піраміду ABCD і знайти:
1) |
® |
® |
® |
напрямні косинуси вектора AB ; 2) кут j між векторами AB і AC ; |
|||
3) |
площу трикутника ABC ; |
|
|
4) |
® ® |
® |
|
об’єм піраміди, побудованої на векторах AB , AC і AD . |
|
||
|
Розв’язання. |
|
|
1) |
® |
|
|
Знайдемо координати вектора AB : |
|
|
|
®
AB = (xB - xA ; yB - yA ; zB - zA )= (1 - 3;2 - (- 2);-4 - 0)= (- 2; 4; - 4).
®
Тепер можемо знайти модуль вектора AB :
®
| AB | = 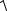 ax 2 + ay 2 + az 2 =
ax 2 + ay 2 + az 2 =  (- 2)2 + 42 + (- 4)2 = 6 .
(- 2)2 + 42 + (- 4)2 = 6 .
Тоді, cosa = |
a |
|
|
= |
- 2 |
= - |
1 |
, cos b = |
ay |
= |
4 |
= |
2 |
, |
||||||
x |
|
|
|
|
|
|
|
|
|
|
||||||||||
® |
|
|
6 |
|
3 |
® |
|
6 |
3 |
|||||||||||
|
| AB |
| |
|
|
|
|
|
|
|
| AB | |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
cosg = |
|
|
az |
= |
- 4 |
= - |
2 |
. |
|
|
|
|
|
|
|
|||||
|
|
® |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
| AB | |
|
6 |
|
|
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
®
2) AС = (xС - xA ; yС - y A ; zС - z A ) = (1 - 3;0 - (- 2);1 - 0)= (- 2; 2;1),
8

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(- 2)2 + 22 + 12 = 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| AС | = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Маємо, AB = (ax ; a y ; az )= (- 2; 4; - 4), |
|
AC = (bx ; by ; bz )= (- 2; 2;1). |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Далі за формулою косинуса кута між двома векторами обчислимо |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
cosj = |
a x bx + a y by + a z bz |
|
= |
- 2 × (- 2)+ 4 × 2 + (- 4)×1 |
= |
4 + 8 - 4 |
|
= |
4 |
. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
® |
|
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 × |
3 |
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
9 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |
AB | ×| AC | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Тому, |
j = arccos |
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
® |
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
3) Обчислимо векторний добуток AB´ AC : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
® |
|
|
® |
|
|
|
® |
|
|
® |
|
|
® |
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
® |
|
|
|
® |
|
|
i |
|
|
|
|
j |
k |
|
|
|
i |
|
j |
|
|
k |
|
® |
|
4 |
|
- 4 |
|
® |
|
- 2 |
|
- 4 |
|
® |
|
- 2 4 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ax |
|
ay |
az |
|
|
- 2 4 - 4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
AB´ AC = |
|
= |
= i |
2 |
|
|
1 |
|
- j |
|
- 2 |
|
1 |
|
+ k |
|
- 2 |
|
2 |
= |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
bx |
|
by |
bz |
|
|
- 2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
® |
((- 2 )× 2 - (- 2 )× 4)= |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
= i (4 ×1 - (- 4 |
)× 2)- j(1× (- 2 )- -(2 × )- 4( ) +)k |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
® |
® |
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
=12 i +10 j |
+ 4 k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
® |
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SDABC = |
1 |
|
|
AB´ AC |
|
= |
1 |
122 |
+102 |
+ 42 = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
|
|
(кв.од.). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
144 + 100 +16 |
260 |
|
65 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
® |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- z A ) = (1 - 3;5 - (- 2);2 - 0)= (- 2; 7; 2), |
|
|
|
||||||||||||||||||||||||||||||||||||||
4) |
AD = (xD - xA ; yD |
- y A ; zD |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
® |
|
|
|
|
|
|
|
|
)= (- 2; 4; - 4) |
® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
AB = (ax ; a y ; az |
, AC = (bx ; by ; bz )= (- 2; 2;1), |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
® |
|
|
|
|
|
|
|
|
)= (- 2; 7; 2), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
AD = (cx ; cy ; cz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
® |
® |
® |
|
ax |
|
|
|
ay |
|
|
|
az |
|
|
|
- 2 4 - 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
bx |
|
|
|
by |
|
|
|
bz |
|
|
|
|
|
- 2 2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
AB AC AD = |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
сx |
|
|
|
сy |
|
|
|
сz |
|
|
|
- 2 |
7 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= -2 |
|
2 1 |
|
- 4 × |
|
- 2 1 |
|
- 4 × |
|
- 2 2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
7 |
2 |
|
|
|
|
- 2 |
|
2 |
|
|
|
|
|
|
|
|
- 2 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= -2 × (- 3)- 4 × (- 2)- 4 × (-10)= 54 .
9

|
|
|
|
Рис.1 |
|
Отже, V пір = |
1 |
® ® ® |
54 |
= 9 (куб.од.). Піраміду ABCD зображено |
|
| AB AC AD | = |
|||||
|
|||||
|
6 |
||||
6 |
|
|
|||
на рис.1. |
|
|
|
||
Запитання до самоконтролю
1.Які величини називаються скалярними? Приклади.
2.Які величини називаються векторними? Приклади.
3.Що таке модуль вектора? Одиничний та нульовий вектори.
4.Що таке розклад вектора за базисом?
5.Як записати вектор в координатній формі, якщо відомі координати його початку A(xA , yA , zA ) і кінця B(xB , yB , zB )?
6.Формула довжини вектора в координатній формі.
7.Напрямні косинуси вектора і їхня властивість.
8.Умова перпендикулярності двох векторів.
9.Запишіть формулу косинуса кута між двома векторами через їхній скалярний добуток.
10.Дайте означення векторного добутку двох векторів.
11.Сформулюйте геометричні властивості векторного добутку.
12.Запишіть формулу обчислення векторного добутку, якщо вектори задано в координатній формі.
13.У якому випадку добуток трьох векторівa, b, c називається міша-
ним? Як позначається мішаний добуток?
14.Який геометричний зміст мішаного добутку?
15.За якою формулою обчислюється мішаний добуток векторів, якщо вони задані в координатній формі?
16.Як виражається необхідна і достатня умови компланарності трьох векторів через їхній мішаний добуток?
10
