17.6. Гіперболічні функції

У розрахунках часто застосовуються гіперболічні функції:

—гіперболічний косинус,

—гіперболічний синус,

—гіперболічний тангенс,

—гіперболічний котангенс.

Графіки гіперболічних функцій наведено на рис. 1 і 2.

Рис. 1

Рис. 2

Гіперболічний функції тісно пов’язані з тригонометричними функціями:

,

. (1)

Із цих формул дістаємо аналогічні залежності:

,

. (2)

Оскільки гіперболічні функції подаються через тригонометричні функції від суто уявного аргументу, то для гіперболічних функцій справджуються формули, аналогічні формулам для тригонометричних функцій.

У формулах для тригонометричних функцій

замінимо на , тоді дістанемо аналогічні формули для гіперболічних функцій:

.

За допомогою гіперболічних функцій можна знаходити значення тригонометричних функцій від комплексних аргументів:

.

Аналогічні формули виконуються для гіперболічних функцій від комплексного аргументу:

17.7. Логарифмічна функція

Логарифмічна функція визначається з рівності

.

Узявши

,

з рівності

знайдемо :

.

Остаточно дістанемо аналітичні вирази для логарифмічної функції:

. (1)

Логарифмічна функція має нескінченну множину значень. Якщо — додатне дійсне число, то всі значення дійсні.

При обході навколо точки у додатному напрямі проти годинникової стрілки набуває додаткового доданка , а функція набуває додаткового доданка .

Приклад. Обчислити: .

• Знайдемо . 

Логарифми від’ємних чисел існують і набувають нескінченної множини комплексних значень.

Приклад. Обчислити: 1) ; 2) .

• ;

2)  . 

Якщо , то для відшукання логарифмів можна використовувати розклад у степеневий ряд:

.

Із цього розкладу можна дістати такий ряд при :

(2)

Уміючи обчислювати логарифми можна визначити показникову функцію з довільною основою за формулою:

. (3)

Приклад. Знайти значення числа і^і, якщо .

• .

Зокрема, при маємо:

.

Приклад. Обчислити .

• Знаходимо значення від’ємного числа в ірраціональному степені:

Знайдені значення всюди щільно лежать на одиничному колі. 

Аналогічно подаються значення степеневої функції за формулою:

(4)

Після обходу навколо початку координат степенева фун­кція набуває додаткового множника . Якщо — ціле число, то і функція є однозначною.

Якщо , то степенева функція при обході навколо початку координат набуває додаткового множника і після обходів повертається до початкового значення, оскільки .

Функція — багатозначна і набуває різних значень, що відрізняються множником

.

Наприклад, функція після першого обходу навколо точки набуває значення , а після другого обходу знову набуває початкового значення .

17.8. Обернені тригонометричні функції

Знайдемо вираз для обернених тригонометричних функцій через логарифмічну функцію.

Функцію можна подати через розв’язок рівняння відносно . Згідно з формулою Ейлера (7) із підрозділу 17.5 знаходимо рівняння . У результаті заміни дістаємо квадратне рівняння:

, ,

, .

Остаточно маємо формулу

. (1)

Приклад. Обчислити значення функції .

• 

Приклад. Обчислити значення функції .

• 

Значення існує, але комплексне. 

Аналогічно знаходимо формулу для з рівняння , . Узявши , дістанемо рівняння або, звідки .

Остаточно маємо:

. (2)

Приклад. Обчислити значення функції .

• 

Приклад. Обчислити значення функції .



Знайдемо аналітичний вираз для . З рівності визначаємо .

Маємо рівняння:

.

У результаті заміни дістаємо рівняння , звідки , .

Остаточно маємо:

. (3)

Приклад. Знайти .

• .

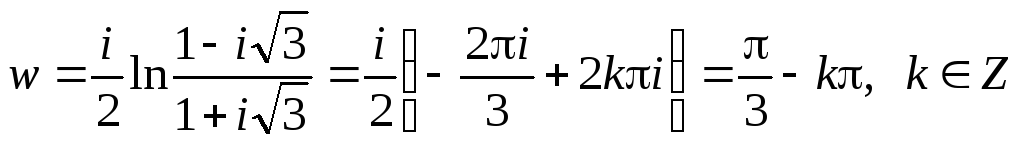Приклад. Обчислити значення функції .

• .

Приклад. Обчислити значення функції .

• 

▲

Насамкінець зауважимо, що функції комплексних змінних мають властивості, які дають змогу обчислювати визначені інтег­рали, розв’язувати задачі математичної фізики, знаходити конформні відображення.

1. Яке число називається уявною одиницею?

2. Що називається дійсною і уявною частиною комплексного числа?

3. Що називається модулем і аргументом комплексного числа?

4. Алгебраїчні дії з комплексними числами.

5. Множення, ділення та піднесення до степеня комплексних чисел у тригонометричній формі.

6. Добування кореня -го степеня.

7. Гіперболічні функції та їх зв’язок із тригонометричними функціями.

8. Логарифми комплексних чисел.

9. Обернені тригонометричні функції комплексного аргу- менту.

1. Обчислити , де .

2. Знайти , де .

3. Знайти .

4. Обчислити .

5. Знайти .

6. Обчислити .

ЛЕКЦІЯ

ОСНОВИ КОМБІНАТОРИКИ ТА ТЕОРІЇ ІМОВІРНОСТЕЙ