Тема 10. Система алгебраїчних рівнянь

10.1. Система лінійних алгебраїчних рівнянь

10.2. Система двох рівнянь з двома невідомими

10.3. Система рівнянь з трьома невідомими

Питання для самоперевірки

Вправи для самостійного розв’язування

10.1. Система лінійних алгебраїчних рівнянь

Основним методом вирішення системи m лінійних алгебраїчних рівнянь з n невідомими являються методом винятку. Опишемо один із варіантів винятку Гаусса.

Це одного рівняння система

,

,

, (1)

наприклад із першого рівняння, надходить невідоме і представляємо в другому рівнянні. В загальному випадку приходимо до системи рівнянь

,

,

. (2)

Останнє m-1 рівняння можна вирішити незалежно від першого рівняння. Із одного рівняння знаходимо і підставимо в останні рівняння. Приходимо до системи рівнянь виду

,

,

,

. (3)

Приклад. Зайдемо вирішення системи рівнянь

,

,

.

Із другого рівняння знаходимо

.

Підставляємо в перше та третє рівняння, знаходимо систему рівнянь

.

Із першого рівняння знаходимо і підставляємо в друге рівняння, одержимо рівняння .

Послідовно знаходимо , , .

Приклад. Знайдемо вирішення системи рівнянь

,

,

.

Із першого рівняння знаходимо

і крім із другого і третього рівнянь, одержимо однакові рівняння

,

.

Звідси знаходимо спільне вирішення системи

Потім вилучається і т. д. Якщо в результаті вилучення одержимо неможливе числове рівняння, то система рівнянь (1) несумісна, так як не має рішення.

Якщо система рівнянь приводиться до вигляду

,

,

,

. (4)

то система рівнянь (1) має єдине рішення, яке знаходиться із системи рівнянь (4), починаючи з останнього рівняння.

Якщо система рівнянь приводиться до вигляду

,

,

, (5)

де .При цьому система рівнянь (1) має нескінченне число рішень. Невідоме являються довільними і називаються вільними. Невідоме називаються базисними. Базисні застосування виражаються через вільне і загальне вирішення системи (1) має вигляд

,

,

. (6)

Часто використовується модифікація методу Гаусса. Якщо невідомі виключаються із всіх рівнянь, то приходимо к системі рівнянь виду

,

,

.

Цей метод виключно називається методом Жордана-Гаусса. При , система управління має єдине рішення.

10.2. Системи двох рівнянь з двома невідомими

Викладемо деякі найбільше уживані способи рішення системи двох рівнянь с двома невідомими.

1. Виняток одного невідомого. Якщо одне із рівнянь системи дозволено відносно одного із невідомих, то знаходимо це невідоме і підставляємо в друге рівняння. При цьому приходимо до одного рівняння з одним невідомим.

Приклад. Знайдемо вирішення системи рівнянь

Перше рівняння розширимо відносно х.

Знаходимо рішення рівняння і відповідне значення .

Приклад. Вирішіть систему рівнянь

;

.

Друге рівняння розв’язно відносно .

Знайдемо і підставимо в перше рівняння. Отримаємо рівняння яке має рішення: . Для невідомого знаходимо відповідне значення: .

Приклад. Знайдемо рішення системи рівнянь

,

.

Якщо розв’язок перших рівнянь відносно , то отримаємо

.

При підстановці цих виразів у друге рівняння отримаємо складне і раціональне рівняння. Помножимо друге рівняння на 2 і складемо перше рівняння. Отримаємо рівняння

лінійне відносно . Знаходимо . Крім із другого рівняння системи приходимо до алгебраїчного рівняння

,

які перетворюються в рівняння

,

які мають розв’язок

.

Знаходимо відповідні значення невідомого .

2. Рішення, основних ненегативних дискримінантів

Нехай кожне рівняння системи рівняння

,

(8)

являється квадратною функцією відносно одного із невідомого, наприклад, . Щоб система (8) мала розв’язок необхідно, щоб дискримінанти рівнянь (8) були негативні, так як

Якщо система нерівностей (9) має рішення , а система рівнянь (8) при має загальний розв’язок , то система рівнянь (8) має розв’язок

Приклад. Розв’язати систему рівнянь

Ці рівняння являються квадратними відносно . Знаходимо дискримінанті рівняння

;

.

Ці нерівності мають єдине загальне рішення . При вихідне рівняння має рішення .

Приклад. Розв’яжемо систему рівнянь

,

.

Ці рівняння є квадратними відносно і мають дискримінанти

,

.

Одержання нерівності мають єдине рішення . При цьому вихідна система має рішення .

3. Однорідні рівняння

Визначення. Функція називається однорідного порядку , якщо виконано торжество

. (10)

Така функція являється однорідною порядку 2, так як виконано торжество

Функція буде однорідною.

Функція буде однорідною нульового порядку.

Постійна величина являється однорідною функцією нульового порядку, так як при . Нуль являється однорідною функцією кожного порядку, так як при кожному .

Визначення. Система алгебраїчних рівнянь

(11)

якщо являється однорідними функціями відповідно порядків

Із системи рівнянь (11) виводиться рівняння

(12)

де — однорідні функції одного порядку. В рівнянні (12) робимо заміну і приходимо до одного рівняння виду

(13)

Якщо знайдене рішення рівняння (13), то система рівнянь (11) розв’язується спільно з рівнянням .

Приклад. Розв’яжіть однорідну систему рівнянь

В першому рівнянні зліва однорідна функція любого порядку. Робимо заміну і приходимо до рівняння

Розв’яжемо систему рівнянь

і знайдемо

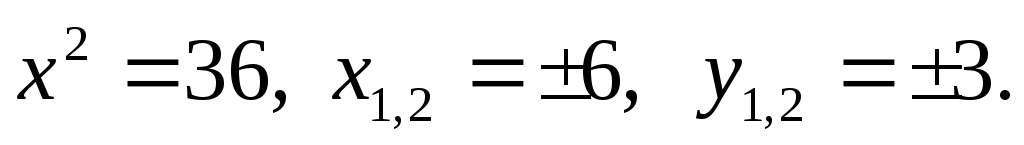
розв’яжемо систему рівня

і знайдемо

Приклад. Розв’яжемо систему рівнянь

Ліва частина рівняння являється однорідними функціями третього порядку. Маємо рівняння

Зліва та справа однорідна функція нульового порядку.

При заміні отримаємо рівняння та його корінь

.

Вирішуючи систему рівнянь

знаходимо рішення

Приклад. Розв’яжемо однорідну систему рівнянь

Поділивши одне рівняння на друге, отримаємо однорідне рівняння

в якому ліва та права частина являється однорідними функціями першого порядку. При , отримаємо рівняння

Яке має розв’язок .

Вирішуючи систему рівнянь

знаходимо два розв’язки: .

Вирішуючи систему рівнянь

Знаходимо рішення:

Вирішуючи систему рівнянь

Знаходимо ще два рішення:

Приклад. Розв’яжемо однорідну систему рівнянь

Ліва частина рівняння являється однорідними функціями другого порядку. Припускаючи отримаємо рівняння

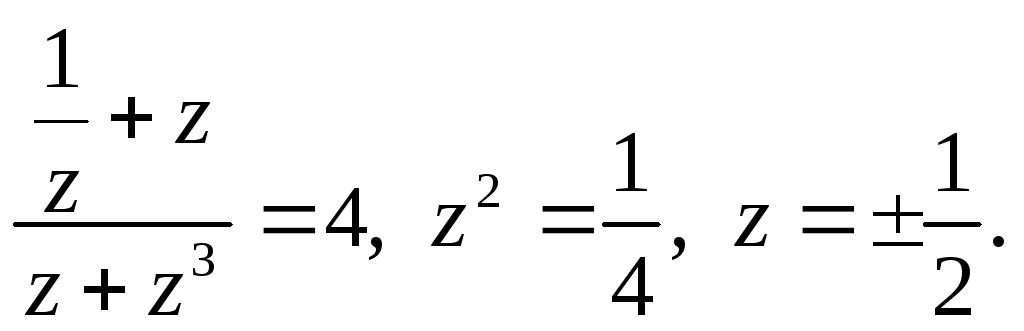
Із системи рівнянь

знаходимо рішення

Система рівнянь

дійсних рішенню не має

4. Симетричні системи рівнянь

Визначення. Функція називається симетричною, якщо виконується торжество .

Система рівнянь

називається симетричною, якщо функція симетрична.

Симетрична система спрощується при використанні симетричної заміни невідомих:

або або і т. д.

Приклад. Розв’яжіть систему рівнянь

Зробимо заміну невідомих

Використавши перетворення

приходимо до системи рівнянь

Із системи рівнянь знаходимо:

Для відшукання маємо систему рівнянь

знаходимо рішення вихідної системи рівнянь

Приклад. Вирішіть систему рівнянь

Зробимо симетричну заміну змінних

та приходимо до системи рівнянь

яка має рішення Для знаходимо систему рівнянь

із якої знаходимо дві системи рівнянь

і розв’язок вихідної системи рівнянь:

Приклад. Розв’яжіть систему симетричних рівнянь

,

Введемо нові невідомі

Виконаємо перетворення

Приходимо до системи рівнянь

Виключимо невідоме . Отримаємо рівняння

яке має рішення . Знаходимо певне значення

Із системи рівнянь

Знаходимо

Із системи рівнянь

Знаходимо

Із системі рівнянь

знаходимо

5. Заміна невідомих

Система алгебраїчних рівнянь часто може бути спрощена, якщо ввести нові значення для невідомих .

Приклад. Розв’яжемо систему рівнянь

Запровадимо значення і прийдемо до системи рівнянь

Із системи рівнянь

Знайдемо рішення вихідної системи

Приклад. Знайдемо рішення системи рівнянь

Запровадимо значення із рівняння

знайдемо рішення

Із системи рівнянь

знайдемо рішення:

Система рівнянь не має вирішення

так як зводиться до рівняння яке не має дійсного рішення.

6. Виключення спільного виразу

Якщо в обох рівнянь системи входить одне і теж вираження, то можна виключити це вираження, тобто з одного рівняння знайти це вираження і підставити в інше рівняння. При цьому може знайтися більш просте рівняння.

Приклад. Розв’яжемо систему рівнянь

Запишемо цю систему рівнянь у вигляді