
elem_mat / R_3
.docТема 3. Радикали. Узагальнення поняття показника
3.1. Властивості ступенів і коренів.
Означення.
Ступенем числа а
з натуральним показником
![]() називається добуток
називається добуток
![]() множників кожної з який дорівнює а.
Ступінь числа а
з показником
множників кожної з який дорівнює а.
Ступінь числа а
з показником
![]() позначають
позначають
![]() ,
наприклад,
,
наприклад,
![]() .
.
У
загальному випадку при
![]() думаємо
думаємо
![]() . (1)
. (1)
Число
![]() називається підставою ступеня, число
називається підставою ступеня, число
![]() називається показником ступеня.
називається показником ступеня.
Приведемо основні властивості дій зі ступенями
-
 .
. -
 .
. -
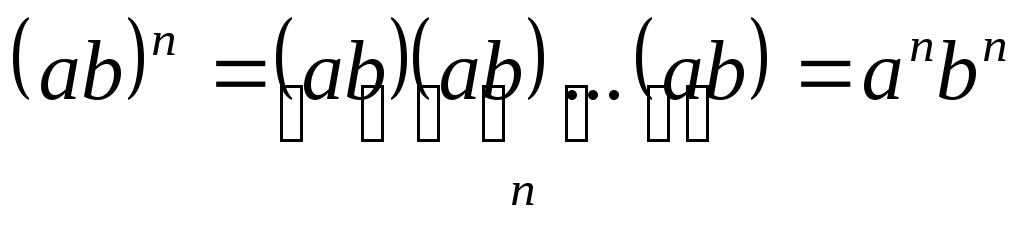 .
. -
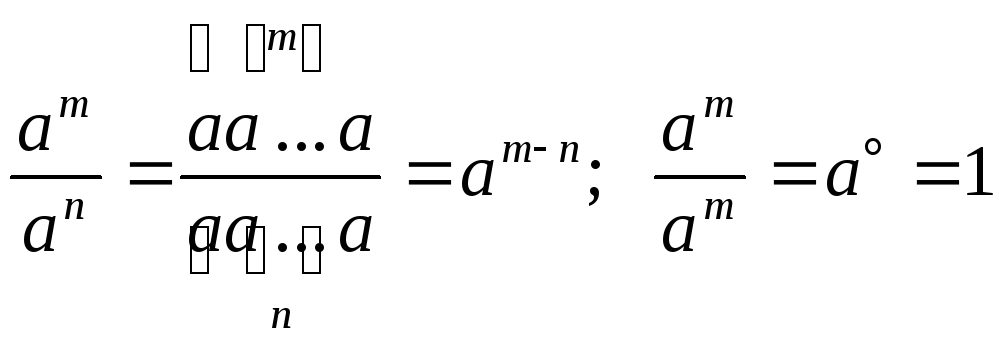 .
. -
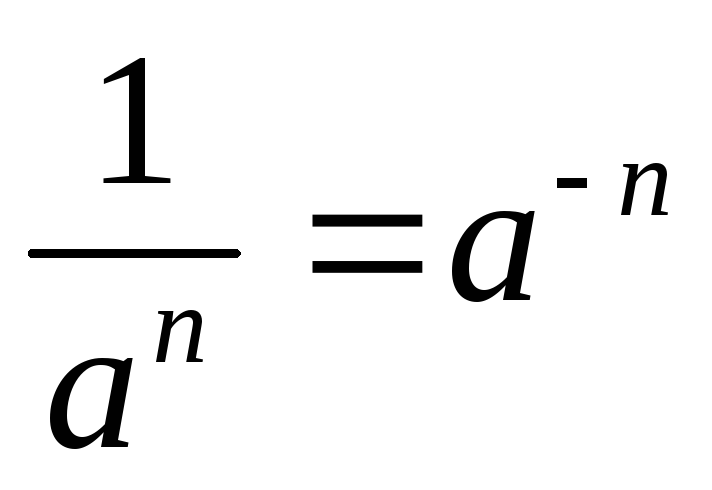 .
. -
 .
(2)
.
(2)
Приведені властивості узагальнюються для будь-яких показників ступеня
1.
![]() ,
4.
,
4.
![]() ,
,
2.
![]() ,
5.
,
5.
![]() ,
,
3.
![]() ,
6.
,
6.
![]() .
(3)
.
(3)
Частина в обчисленнях використовуються ступені з раціональним показником. При цьому виявилося зручним наступне позначення
![]() . (4)
. (4)
Означення.
Коренем
![]() -й
ступеня з числа
-й
ступеня з числа
![]() називається число
називається число
![]() ,
,
![]() -я
ступінь якого дорівнює
-я
ступінь якого дорівнює
![]() :
:
![]() . (5)
. (5)
Корінь також називається радикалом.
Корінь
непарного ступеня
![]() завжди існує. Корінь парного ступеня
завжди існує. Корінь парного ступеня
![]() з негативного числа не існує. Існують
два протилежних числа, що є коренями
парного ступеня з позитивного числа
з негативного числа не існує. Існують
два протилежних числа, що є коренями
парного ступеня з позитивного числа
![]() .
Позитивний корінь позначається
.
Позитивний корінь позначається
![]() ,
протилежний корінь позначається
,
протилежний корінь позначається
![]() .
.
Ненегативний
корінь
![]() -ой
ступеня з ненегативного числа називають
арифметичним коренем.
-ой
ступеня з ненегативного числа називають
арифметичним коренем.
З формул (3), (4) випливають наступні властивості радикалів
-
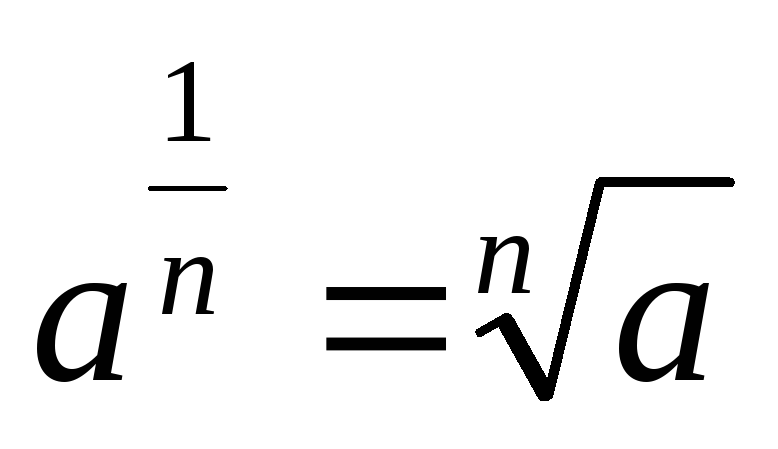 . 7.
. 7.
 .
. -
 . 8.
. 8.
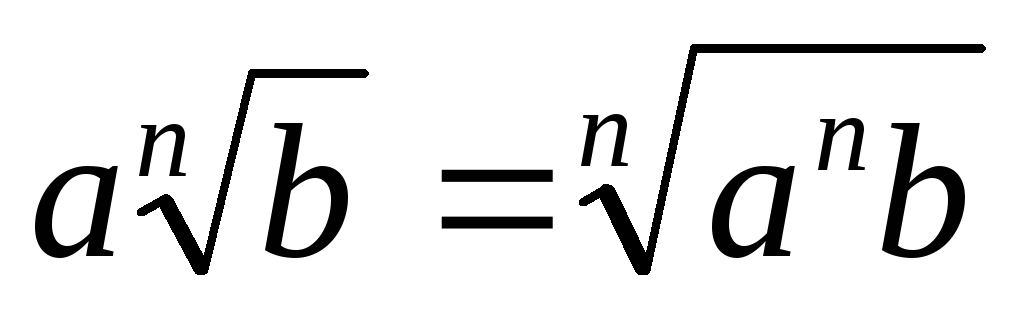 .
. -
 . 9.
. 9.
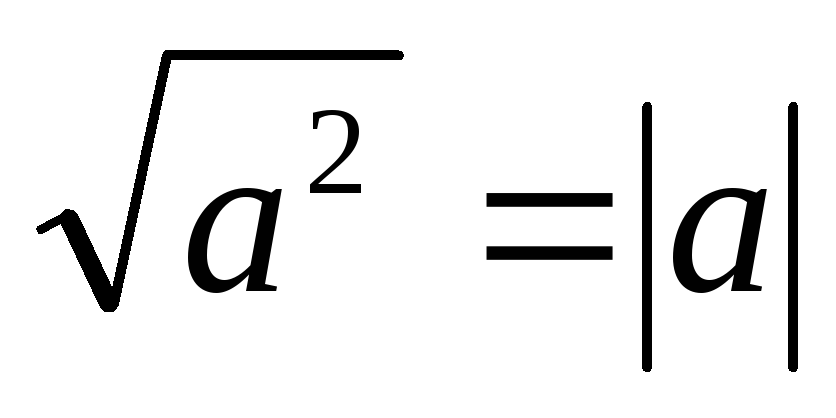 .
. -
 . 10.
. 10.
 .
. -
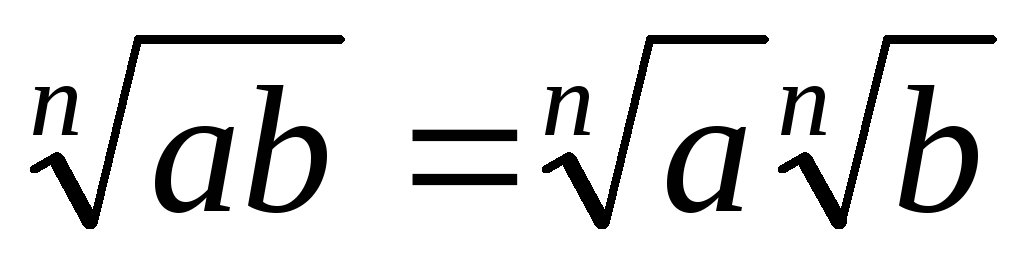 . 11.
. 11.
 .
. -
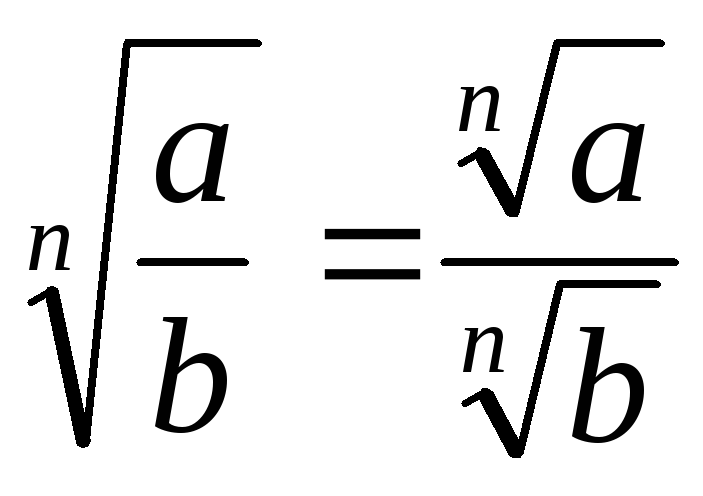 . 12.
. 12.
 .
(6)
.
(6)
Якщо
ступінь кореня
![]() ,
то показник кореня звичайно не пишеться.
,
то показник кореня звичайно не пишеться.
Приклад.
Знайти значення вираження
![]() .
.
Підкореневе вираження розкладемо на прості множники
![]() .
.
Приклад.
Спростити вираження
![]() при
при
![]() .
Маємо:
.
Маємо:
![]() .
.
Приклад.
Витягти корінь
![]() при
при
![]() .
Маємо:
.
Маємо:
![]() .
.
Приклад.
Спростити вираження
![]() при
при
![]() .
Оскільки при
.
Оскільки при
![]()
![]()
![]() .
.
3.2. Дії з радикалами
Перетворення кореня по формулі
![]() (7)
(7)
називається внесенням множника під знак радикала.
Приклад.
Внести множник під знак кореня
![]() .
.
По
формулі (7) одержимо
![]() .
.
Приклад.
Внести множник під знак радикала
![]() при
при
![]() .
Маємо рівність
.
Маємо рівність
![]() .
.
Перетворення кореня по формулі
![]()
називається винесенням множника з під знака радикала.
Приклад.
Винести множник з під знака кореня у
вираженні
![]() при
при
![]() .
Одержимо рівність
.
Одержимо рівність
![]() .
.
Приклад.
Винести множник з під знака кореня
![]() при
при
![]() .
Маємо:
.
Маємо:
![]() .
.
Приклад. Винести множник з під знака коренів:
![]() .
.
![]() .
.
![]() .
.
Радикали
виду
![]() ,
де
,
де
![]() — раціональні числа, називаються
подібними. Їх можна складати і віднімати
— раціональні числа, називаються
подібними. Їх можна складати і віднімати
![]() .
.
Приклад. Спростити:
![]() .
.
Приклад. Скласти радикали:
![]()
![]() .
.
Приклад. Спростити:
![]()
![]() .
.
Слід зазначити, що невірно формулу
![]() ,
,
що видно на прикладі
![]() .
.
Приведемо приклади множення радикалів.
Приклади.
![]() ,
,
![]() .
.
Аналогічно звільняються від кубічних ірраціональностей у знаменнику
 ;
;
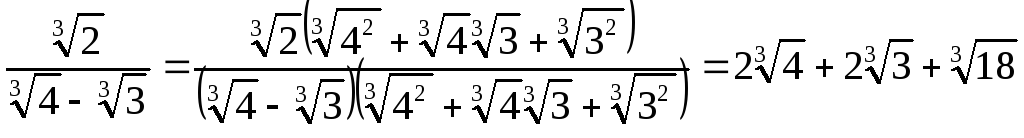 .
.
Розглянемо більш складні приклади раціоналізації знаменників
![]()
![]() ;
;
![]()
![]() .
.
При перемножуванні радикалів з різними показниками ступеня і спочатку перетворять у радикали з однаковими показниками.
Приклад. Перемножимо радикали
![]()
![]() .
.
При перемножуванні радикалів можна використовувати формули скороченого множення. Наприклад:
![]() ;
;
![]() ;
;
![]() .
.
Якщо радикали знаходяться в знаменнику дробу, то, використовуючи властивості радикалів, можна звільнитися від ірраціональності в знаменнику.
Приклад. Раціоналізуємо знаменники дробів
![]()
![]() .
.
![]() ;
;
![]() .
.
Вираження
![]() називаються сполученими. Добутку
сполучених виражень не містить радикалів
називаються сполученими. Добутку
сполучених виражень не містить радикалів
![]() .
.
Ця властивість використовується для раціоналізації знаменників.
Приклад. Звільнитися про ірраціональність у знаменнику
![]() ;
;
![]() ;
;
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Звільнимося від ірраціональності в знаменнику дробу
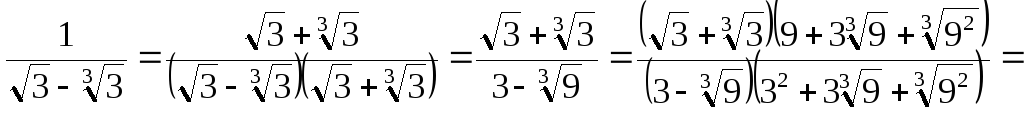
![]() .
.
3.3. Обчислення ірраціональних виражень
За допомогою властивостей коренів треба спростити й обчислити ірраціональне вираження.
Приклад. Обчислити вираження

Виконаємо послідовно дії:
-
 .
. -
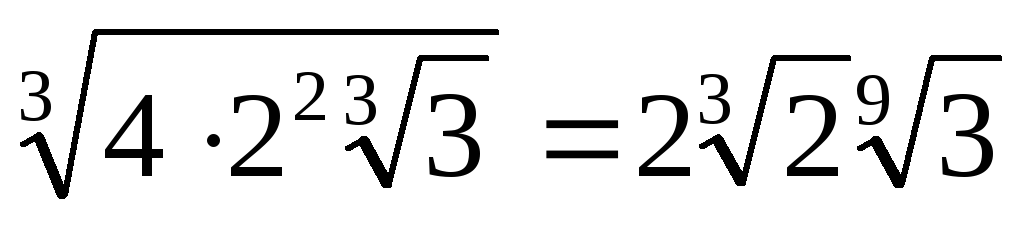 .
. -
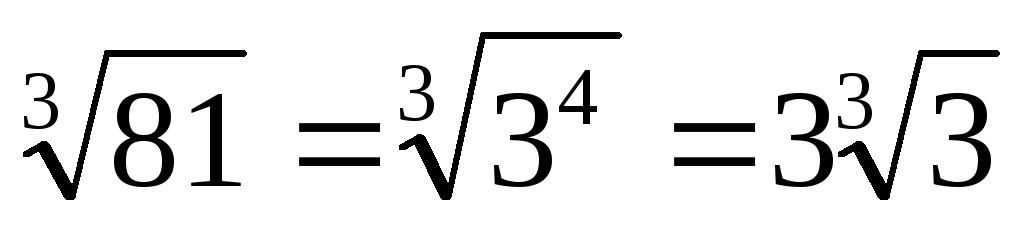 .
. -
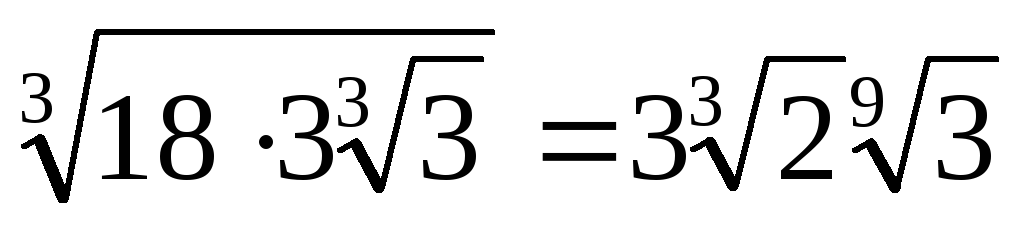 .
. -
 .
. -
 .
. -
 .
. -
 .
. -
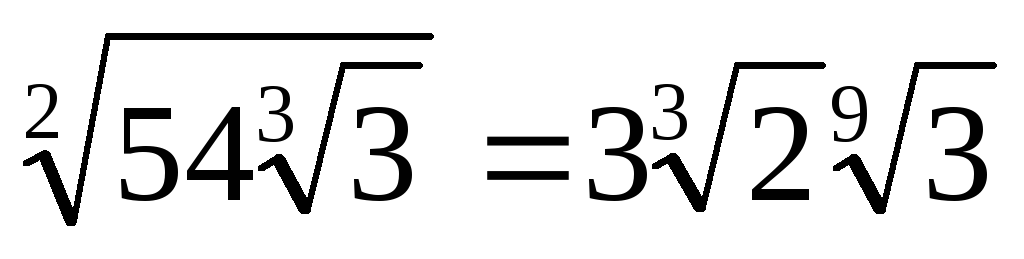 .
. -
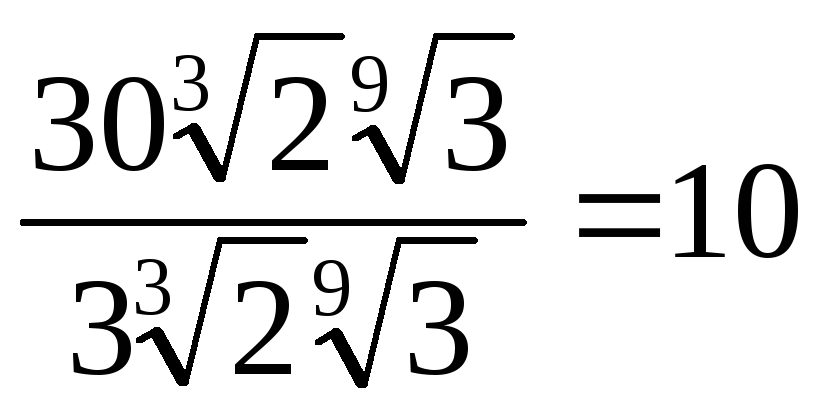 .
.
Приклад. Обчислити вираження:
![]()
Виконаємо дії.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Часто використовується формула подвійного радикала
![]() (8)
(8)
Приклад. По формулі (8) знаходимо
![]() .
.
![]() .
.
Приклад.
Обчислити вираження
![]()
По формулі (8) знаходимо
![]() ;
;
![]() .
.
Остаточно одержимо:
![]() .
.
Аналогічно обчислюються кубічні корені. Думаємо:
![]() ,
,
зводимо
рівність у куб.![]()
Дорівнюючи
вираження при
![]() ,
одержимо однорідну систему рівнянь
,
одержимо однорідну систему рівнянь
![]() .
.
Поділивши
рівняння, приходимо до рівняння для
![]()
![]() .
.
Якщо
![]() — раціональні числа, то
— раціональні числа, то
![]() знаходиться з рівняння (9).
знаходиться з рівняння (9).
Приклад. Обчислимо значення радикала
![]() .
.
Після зведення в куб рівняння, приходимо до системи рівнянь
![]() .
.
Поділивши
перше рівняння на друге, одержимо
рівняння для
![]()
![]() .
.
За схемою
Торнера знаходимо корінь
![]() .
.
Із
системи рівнянь і рівняння
![]() знаходимо
знаходимо
![]() .
Отже
.
Отже
![]() .
.
Приклад.
Обчислити
![]() .
.
Покладемо
![]() .
Зводячи рівняння в куб, приходимо до
рівняння
.
Зводячи рівняння в куб, приходимо до
рівняння
![]() ,
з якого одержимо систему рівнянь
,
з якого одержимо систему рівнянь
![]() .
.
Система
рівнянь має очевидне рішення
![]() .
.
Тому
![]() .
Обчислюємо радикал
.
Обчислюємо радикал
![]() .
.
Остаточно
одержимо
![]() .
.
Приклад.
Обчислити
![]() .
Оскільки
.
Оскільки
![]() ,
те думаємо
,
те думаємо
![]() .
.
![]()
![]() .
.
Одержимо
![]() .
.
Приклад.
Обчислити вираження
![]() .
Зведемо рівняння в куб, використовуючи
рівність
.
Зведемо рівняння в куб, використовуючи
рівність
![]() .
.
Одержимо
для
![]() кубічне рівняння
кубічне рівняння
![]() чи
чи
![]() .
Це рівняння має корені
.
Це рівняння має корені
![]() .
.
Тому
![]() — дійсний корінь,
— дійсний корінь,
![]() .
.
3.4. Оцінки для радикалів
Якщо
![]() то
то
![]() чи
чи
![]() . (10)
. (10)
Це нерівність можна використовувати для доказу нерівностей для радикалів.
Приклад.
Довести, що
![]() .
Піднесемо нерівність до шосту степеня
й одержимо очевидну нерівність
.
Піднесемо нерівність до шосту степеня
й одержимо очевидну нерівність
![]() .
.
Можна перетворити радикали до одного показника ступеня
![]() .
.
Оскільки
![]() ,
те
,
те
![]() .
.
Приклад.
Оцінимо
![]() .
Оскільки
.
Оскільки
![]() ,
те
,
те
![]() ,
отже,
,
отже,
![]() .
.
При
перебуванні нерівностей можна
використовувати символ V, розуміючи під
ним
![]() чи знаки
чи знаки
![]() ,
чи
,
чи
![]() .
.
Приклад.
Установити, яке число
![]() чи більше
чи більше
![]() .
.
Рішення.
![]() ,
,
![]() .
.
Оскільки
![]() ,
те
,
те
![]() .
.
Іншим джерелом для нерівностей є відомі класичні нерівності.
Приведемо нерівність Коші
![]() , (11)
, (11)
і більш загальна нерівність
![]() . (12)
. (12)
Приведемо нерівність Коши-Буняковського
![]() . (13)
. (13)
При
![]() одержимо нерівність
одержимо нерівність
![]() .
.
Якщо
![]() ,
то маємо оцінку
,
то маємо оцінку
![]() .
.
Приклад.
При
![]() маємо оцінку
маємо оцінку
![]() .
.
Наближене
значення
![]() знаходиться по формулі
знаходиться по формулі
![]() . (14)
. (14)
Приклад.
Знайдемо значення
![]() по формулі (14).
по формулі (14).
Нехай
![]() .
Знаходимо послідовно при
.
Знаходимо послідовно при
![]()
![]()
![]()
![]()
![]() .
.
Отже
![]() .
.
При
відшуканні
![]() можна використовувати метод Ньютона
для рішення рівняння
можна використовувати метод Ньютона
для рішення рівняння
![]() .
Одержимо обчислювальну схему
.
Одержимо обчислювальну схему
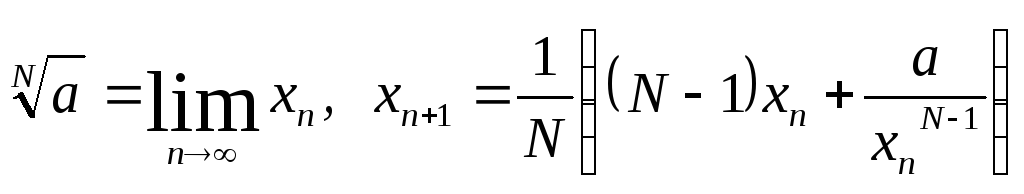 . (15)
. (15)
Приклад.
Знайдемо
![]() .
З формули (15) одержимо
.
З формули (15) одержимо
![]() .
.
Одержимо:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Отже,
![]() .
.
Аналогічно
знаходяться корені будь-якого ступеня.
Відзначимо, що, як правило, корені не
можна точно виразити десятковим дробом.
Звичайно корені є ірраціональними
числами, тобто не можуть бути представлені
дробом
![]() ,
де
,
де
![]() — цілі числа.
— цілі числа.
Приклад.
Доведемо, що
![]() є ірраціональним числом. Припустимо
противне. Нехай
є ірраціональним числом. Припустимо
противне. Нехай
![]() ,
де
,
де
![]() — взаємно прості цілі числа. Одержимо
— взаємно прості цілі числа. Одержимо
![]() .
Оскільки
.
Оскільки
![]() поділяється на 2, те і число
поділяється на 2, те і число
![]() поділяється на 2. Покладемо
поділяється на 2. Покладемо
![]() ,
де
,
де
![]() — ціле число.
— ціле число.
![]() Чи
одержимо
Чи
одержимо
![]() .
Звідси випливає, що число і поділяється
на 2. Це суперечить припущенню, що
.
Звідси випливає, що число і поділяється
на 2. Це суперечить припущенню, що
![]() — взаємно прості числа. Отже, представлення
виду
— взаємно прості числа. Отже, представлення
виду
![]() ,
де
,
де
![]() — взаємно прості цілі числа, неможливо.
— взаємно прості цілі числа, неможливо.
Вправи для самоперевірки
-
Що називається ступенем числа з натуральним показником.
-
Властивості ступенів.
-
Що називається коренів
 -ой
ступеня з числа
-ой
ступеня з числа
 .
. -
Що називається арифметичним коренем.
-
Властивості радикалів.
Вправи для самостійного розв'язування
Спростити числовий вираз
-
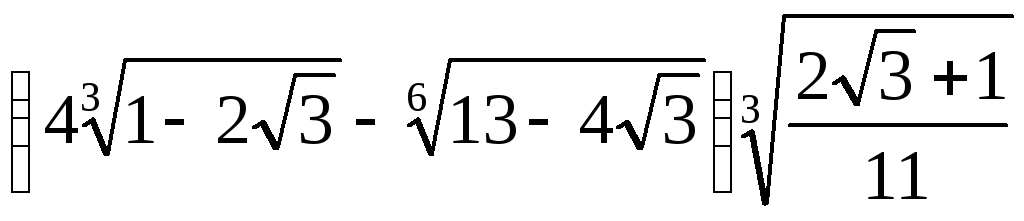 (–3).
(–3). -
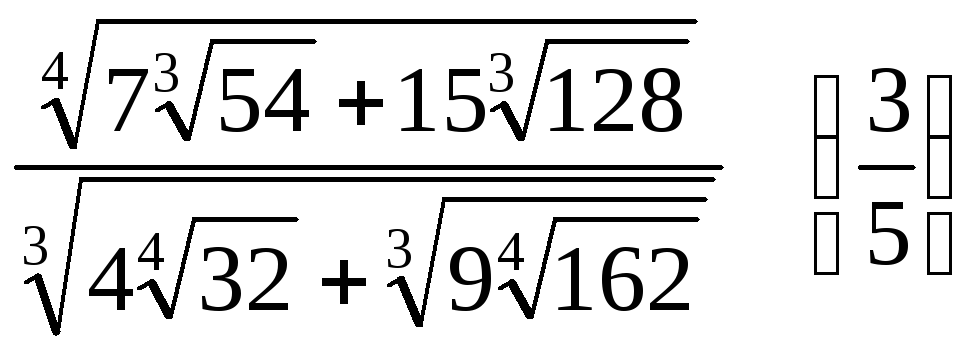 .
. -
 (0).
(0). -
 .
. -
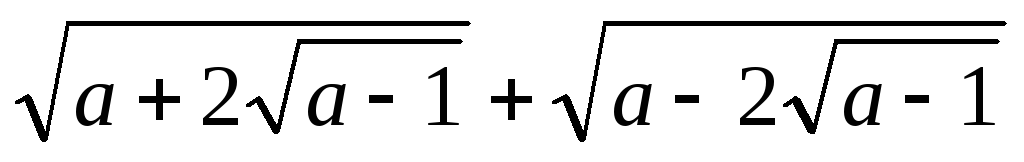
![]() .
.
Перевірити справедливість рівностей
-
 .
. -
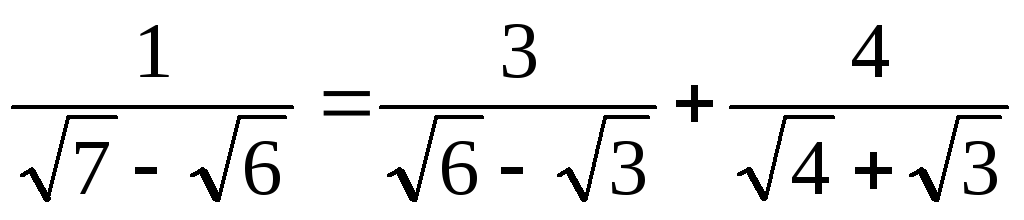 .
. -
 .
. -
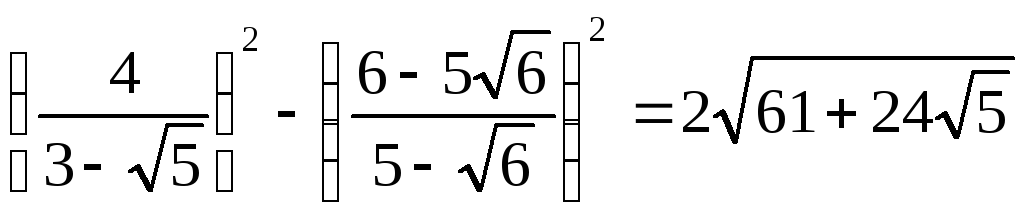 .
. -
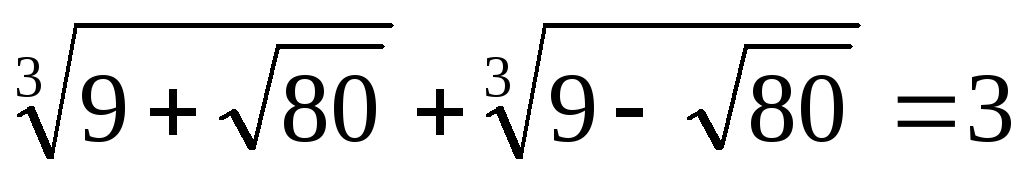 .
. -
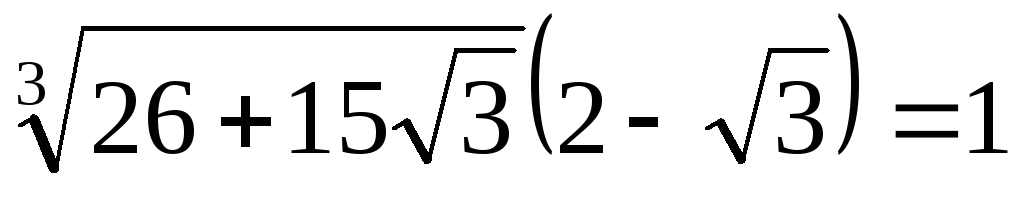 .
. -
 .
. -
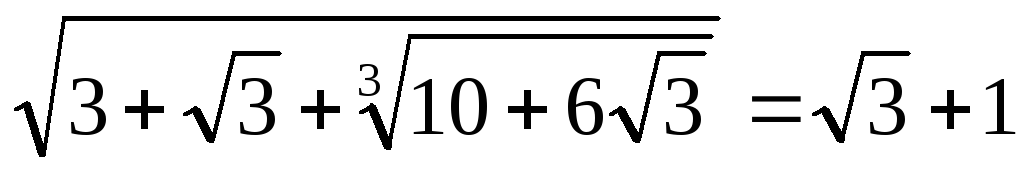 .
. -
 .
. -
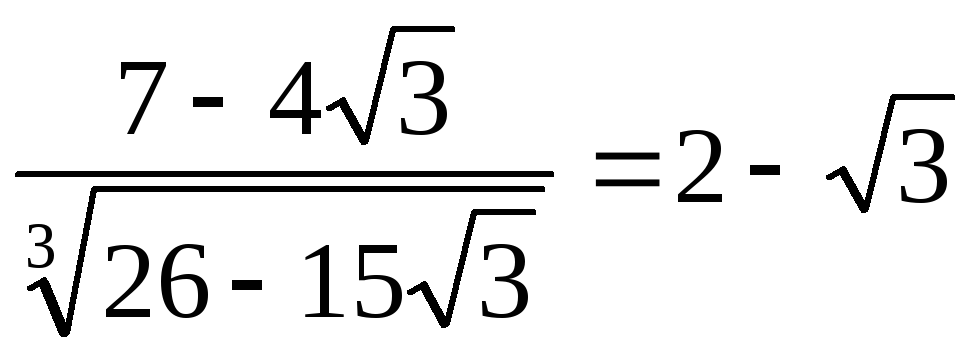 .
.
