Классификация точек разрыва функций

1. Устранимый разрыв.

Точка а называется точкой устранимого разрыва функции , если предел функции в этой точке существует, но в точке а функциялибо не определена, либо ее значениене равно пределу в этой точке

2. Разрыв первого рода.

Точка а называется точкой разрыва первого рода функции , если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы.

3. Разрыв второго рода.

Точка а называется точкой разрыва второго рода функции Точка а называется точкой устранимого разрыва функции , если в этой точке функция не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

25. Производная: определение, механический и геометрический смысл. Уравне-ние касательной к кривой.

Определение производной

Пусть функция 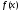определена на некотором промежутке Х. Придадим значению аргумента в точке произвольное приращение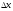 так, чтобы точка также принадлежала Х. Тогда соответствующее приращение функции 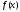составит .

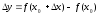Опр. Производной функции в точкеназывается предел отношения приращения функции в этой точке к приращению аргумента при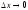(если этот предел существует).

Если в некоторой точке предел бесконечен, то говорят, что в этой точке функция имеет бесконечную производную. Если функция имеет производную в каждой точке множества Х, то производнаятакже является функцией от аргумента х, определенной на Х.

Геометрический смысл производной

Для выяснения геометрического смысла производной нам понадобится определение касательной к графику функции в данной точке.

Опр. Касательной к графику функции в точке М называется предельное положение секущей МN, когда точка N стремится к точке М по кривой.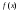

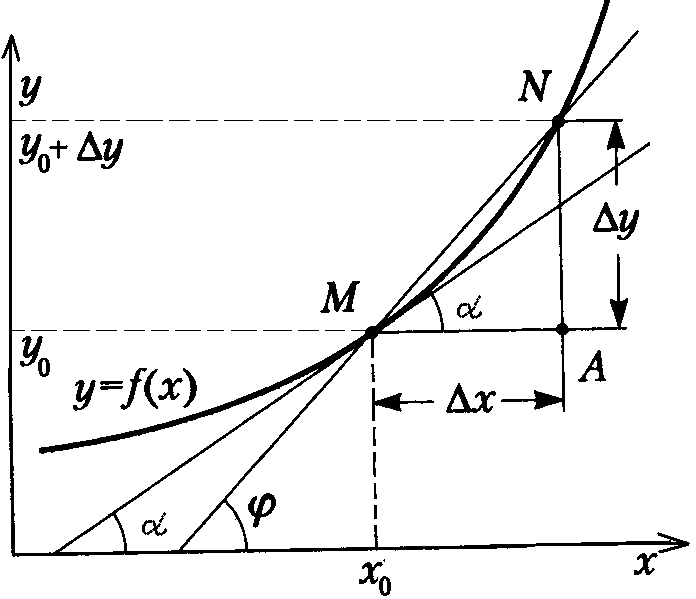
Уравнение пучка прямых, проходящих через точку 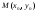, имеет вид

Угловой коэффициент секущей равен

Тогда угловой коэффициент касательной равен

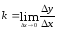
Отсюда следует наглядный вывод о том, что 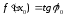. В этом и состоитгеометрический смысл производной.

• Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ + 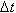точка перемещается на расстояние:x ( t₀ + ) -x ( t₀ ) = , а еёсредняя скорость равна:  v_a =  /  . При  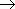0  значение средней скорости стремится к определённой величине, которая называетсямгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:  

• отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной.Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

Уравнение касательной к графику функции в точке имеет вид: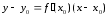

26. Основные правила дифференцирования. Производные основных элементар-ных функций.

Правила дифференцирования.

1. Производная постоянной равна нулю

.

2. Производная аргумента равна единице.

.

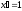3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций.

.

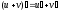1. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго.

Следствие 1. Постоянный множитель можно выносить за знак производной.

.

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например

.

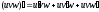5. Производная частного двух дифференцируемых функций может быть найдена по формуле:

Производные основных элементар-ных функций.

1. (C)” = 0, где C = const

2. (x^a)” = ax^a-1, где a не равно 0

3. (a^x)” = a^xln a, где a > 0

4. (e^x)” = e^x

5. (log_a ^x)” =1/x ln_a, где a > 0

6. (ln x)” =1/x

7. (sin x)” = cos x

8. (cos x)” = - sin x

9. (tg x)” =1/cos²x

10. (ctg x)” = -1/sin²x

11. (arcsin x)” = 1/~1-x²

12. (arccos x)’ = -1/~1-x²

13. (arctg x)” =1/1+x²

14. (arcctg x)” = -1/1+x²

27. Производная сложной функции. Производные высших порядков.