- •Операции над множествами
- •Основные свойства функций.
- •Основные элементарные функции. Их свойства и графики
- •1. Линейная функция.
- •Свойства линейной функции
- •2. Квадратичная функция.
- •3. Показательная функция.
- •4. Логарифмическая функция
- •6. Степенная функция
- •Пример использования функций в экономике.
- •Предел функции в бесконечности и точке
- •Теоремы о пределах функций
- •Два замечательных предела
- •Свойства функций, непрерывных в точке
- •Классификация точек разрыва функций
- •Определение производной
- •Геометрический смысл производной
- •Производная сложной функции
Теоремы о пределах функций
Пусть
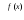 и
и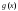 -
функции, для которых существуют пределы
при
-
функции, для которых существуют пределы
при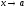 :
: ,
,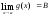 .
.
Функция не может иметь более одного предела.
Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций.
Предел произведения конечного числа функций равен произведению пределов этих функций. В частности постоянный множитель можно выносить за знак предела.
Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю).
Теорема.
Пусть функции
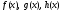 определены в некоторой окрестности
точки а, за исключением быть может самой
точки а, и функции
определены в некоторой окрестности
точки а, за исключением быть может самой
точки а, и функции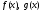 имеют
в этой точке предел, равный А
имеют
в этой точке предел, равный А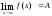 ,
, .
Кроме того, пусть выполнены неравенства:
.
Кроме того, пусть выполнены неравенства: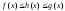 .
Тогда
.
Тогда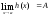
22. Первый замечательный предел. Второй замечательный предел.
Два замечательных предела
Теорема
(первый замечательный предел). Предел
функции
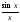 в точкеx=0
существует и равен единице, т.е
в точкеx=0
существует и равен единице, т.е
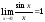 .
.
Теорема
(второй замечательный предел). Предел
функции
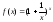 приx
стремящемся к бесконечности существует
и равен е,
т.е.
приx
стремящемся к бесконечности существует
и равен е,
т.е.

23. Непрерывность функции. Свойства функций, непрерывных в точке.
Понятие непрерывности функции является фундаментальным в математическом анализе.
Опр.
Функция
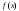 называется непрерывной в точке а, если:
называется непрерывной в точке а, если:
она определена в точке а;
имеет конечный предел при
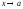 ;
;предел этой функции в точке а и ее значение в этой точке равны, т.е.
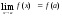 .
.
Опр.
Функция
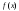 называется непрерывной справа (слева)
в точке а, если правый (левый) предел
этой функции в точке а и ее значение в
этой точке равны, т.е.
называется непрерывной справа (слева)
в точке а, если правый (левый) предел
этой функции в точке а и ее значение в
этой точке равны, т.е.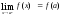 ,
,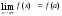 .
.
Если функция непрерывна в точке а и слева, и справа, то она непрерывна в этой точке.
Точки, в которых функция не является непрерывной называются точками разрыва.
Теорема.
Пусть функции
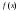 и
и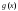 непрерывны в точке а. Тогда функции
непрерывны в точке а. Тогда функции ,
,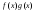 ,
,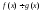 также непрерывны в точке а (частное при
условии
также непрерывны в точке а (частное при
условии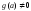 .
.
Свойства функций, непрерывных в точке
Поскольку
точки ![]() непрерывности
функции
непрерывности
функции ![]() задаются
условием
задаются
условием ![]() ,
то часть свойств функций, непрерывных
в точке
,
то часть свойств функций, непрерывных
в точке ![]() ,
следует непосредственно из свойств
пределов. Сформулируем их в виде следующей
теоремы
,
следует непосредственно из свойств
пределов. Сформулируем их в виде следующей
теоремы
Теорема 3.1 Пусть
функции ![]() и
и![]() непрерывны
в точке
непрерывны
в точке![]() .
Тогда функции
.
Тогда функции![]() ,
,![]() ,
,![]() непрерывны
в точке
непрерывны
в точке![]() .
Если
.
Если![]() ,
то функция
,
то функция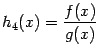 также
непрерывна в точке
также
непрерывна в точке![]() .
.
Доказательство. Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.
Как непосредственное следствие этой теоремы получается следующее
Предложение 3.3 Рассмотрим
множество всех функций, определённых
в некоторой фиксированной
окрестности ![]() точки
точки ![]() и
непрерывных в этой точке. Тогда это
множество
и
непрерывных в этой точке. Тогда это
множество ![]() является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
является
линейным пространством, то есть замкнуто
относительно сложения и умножения на
постоянные:
![]()
Доказательство. Действительно, постоянные
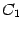 и
и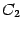 --
это непpеpывные функции (в любой точке);
по пpедыдущей теоpеме тогда непpеpывны
в точке
--
это непpеpывные функции (в любой точке);
по пpедыдущей теоpеме тогда непpеpывны
в точке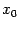 пpоизведения
пpоизведения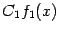 и
и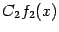 .
Но тогда по этой же теоpеме непpеpывна
в точке
.
Но тогда по этой же теоpеме непpеpывна
в точке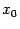 и
сумма
и
сумма
Теорема 3.2 Пусть
функции ![]() и
и ![]() таковы,
что существует композиция
таковы,
что существует композиция ![]() ,
, ![]() .
Пусть функция
.
Пусть функция ![]() непрерывна
в точке
непрерывна
в точке ![]() ,
а функция
,
а функция ![]() непрерывна
в соответствующей точке
непрерывна
в соответствующей точке ![]() .
Тогда композиция
.
Тогда композиция ![]() непрерывна
в точке
непрерывна
в точке ![]() .
.
Доказательство. Заметим, что равенство
 означает,
что при
означает,
что при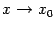 будет
будет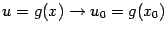 .
Значит,
.
Значит,
![]()
(последнее
равенство следует из непрерывности
функции ![]() в
точке
в
точке ![]() ).
Значит,
).
Значит,
![]()
а
это равенство означает, что
композиция ![]() непрерывна
в точке
непрерывна
в точке ![]() .
.
Заметим, что, очевидно, в предыдущих двух теоремах можно было бы заменить базу
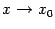 на
односторонние базы
на
односторонние базы или
или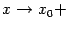 и
получить аналогичные утверждения для
непрерывности слева или справа:
и
получить аналогичные утверждения для
непрерывности слева или справа:
Теорема 3.3 Пусть
функции ![]() и
и![]() непрерывны
слева (справа) в точке
непрерывны
слева (справа) в точке![]() .
Тогда функции
.
Тогда функции![]() ,
,![]() ,
,![]() непрерывны
слева (соотв. справа) в точке
непрерывны
слева (соотв. справа) в точке![]() .
Если
.
Если![]() ,
то функция
,
то функция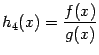 также
непрерывна слева (спpава) в точке
также
непрерывна слева (спpава) в точке![]() .
.
Теорема 3.4 Пусть
функция ![]() непрерывна
слева (справа) в точке
непрерывна
слева (справа) в точке ![]() ,
а функция
,
а функция ![]() непрерывна
в точке
непрерывна
в точке ![]() .
Тогда композиция
.
Тогда композиция ![]() непрерывна
слева (соотв. справа) в точке
непрерывна
слева (соотв. справа) в точке ![]() .
.
24. Точки разрыва функции. Их классификация.
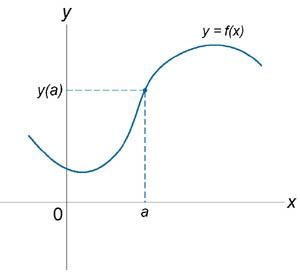
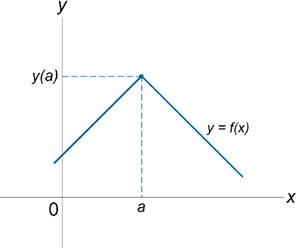
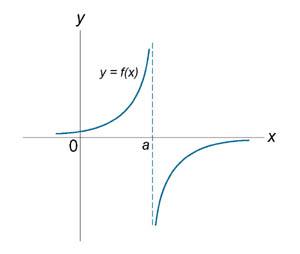
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
|
|
|
|
|
Непрерывна при x = a.
|
|
Имеет разрыв при x = a.
|
|
|
|
|
|
Непрерывна при x = a. |
|
Имеет разрыв при x = a. |
|
Рисунок 1. | ||