
- •Операции над множествами
- •Основные свойства функций.
- •Основные элементарные функции. Их свойства и графики
- •1. Линейная функция.
- •Свойства линейной функции
- •2. Квадратичная функция.
- •3. Показательная функция.
- •4. Логарифмическая функция
- •6. Степенная функция
- •Пример использования функций в экономике.
- •Предел функции в бесконечности и точке
- •Теоремы о пределах функций
- •Два замечательных предела
- •Свойства функций, непрерывных в точке
- •Классификация точек разрыва функций
- •Определение производной
- •Геометрический смысл производной
- •Производная сложной функции
3. Показательная функция.
Функция
вида
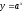 ,
где
,
где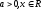 называетсяпоказательной
функцией.
называетсяпоказательной
функцией.
Коэффициент а - положительное число, указывает на возрастание или убывание функции.
Свойства функции:
1. Д(у)=R.
2. Е(у)=
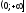 .
.
3. Функция возрастает (а>1), убывает (а<1) на всей области определения.
4. График функции пересекает ось ординат в точке (0;1).
5. Функция непрерывна
на всей области определения, дифференцируема
и производная равна
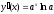 .
.
4. Логарифмическая функция
Логарифмической
функцией
называется
функция вида
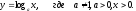
Число а определяет расположение графика.
Вместо логарифмической
функции с произвольным основанием
удобно рассматривать функцию вида
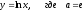 .
.
Так как
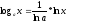 ,
то указанные функции исчерпывают все
логарифмические функции.
,
то указанные функции исчерпывают все
логарифмические функции.
Свойства функции у=ln x.
1. Д(у)=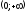 .
.
2. Е(у)=R.
3. Функция принимает нулевое значение при х=1.
4. Функция возрастает на всей области определения.
5. Функция является
непрерывной на всей области определения,
дифференцируема и
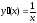 .
.
 5.
Экспоненциальная функция
5.
Экспоненциальная функция
Функция,
обратная функции
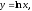 называется
экспоненциальной
и
записывается
уравнением
называется
экспоненциальной
и
записывается
уравнением
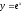 .
.
График функции
симметричен графику функции
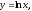 (см. рис.22) относительно прямой у=х.
(см. рис.22) относительно прямой у=х.
Свойства функции: (смотри свойства показательной функции).
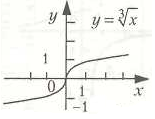
6. Степенная функция
Степенной
функцией с
действительным показателем называется
функция вида
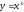 , где b-действительное число, х>0.
, где b-действительное число, х>0.
Примеры степенных
функций:
 .
.
Коэффициент b определяет положение графика на координатной плоскости.
Свойства функции.
1. Функция определена для х>0.
2. Е(у)=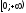 .
.
3. Функция возрастающая, если b>0 и убывающая, если b<0.
4. Функция непрерывна
на всей области определения, дифференцируемая
и
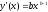 .
.
Пример использования функций в экономике.
Функции находят широкое применение в экономической теории и практике. Спектр используемых в экономике функций весьма широк: от простейших линейных до функций, получаемых по определенному алгоритму с помощью так называемых рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени.
Наряду с линейными используются нелинейные функции: дробно-рациональные, степенные (квадратичная, кубическая и т.д.). показательные (экспоненциальные), логарифмические и др. Периодичность, колеблемость ряда экономических процессов позволяет также применять тригонометрические функции.
Наиболее часто в экономике используются следующие функции.
Функция полезности (функция предпочтений) — в широком смысле зависимость полезности, т.е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия.
Производственная функция — зависимость результата производственной деятельности от обусловивших его факторов.
Функция выпуска (частный вид производственной функции) — зависимость объема производства от наличия или потребления ресурсов.
Функция издержек (частный вид производственной функции) — зависимость издержек производства от объема выпуска продукции.
Функции спроса, потребления, предложения — зависимость объема спроса, потребления, предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.)
20. Предел функции в бесконечности и точке.
Предел функции в бесконечности и точке
С понятием предела числовой последовательности тесно связано понятие предела функции в бесконечности. Если в первом случае переменная n, возрастая, принимает лишь натуральные значения, то во втором случае переменная x, изменяясь, принимает любые значения.
Опр.
Число А называется пределом функции
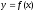 приx,
стремящемся к бесконечности, если для
любого
приx,
стремящемся к бесконечности, если для
любого
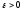 существует такое положительное числоS
(зависящее только от
существует такое положительное числоS
(зависящее только от
 ),
что при всех
),
что при всех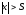 выполняется неравенство
выполняется неравенство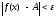
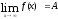 .
.
Пусть
функция
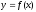 задана в окрестности точкиа,
кроме, быть может, самой точки а.
задана в окрестности точкиа,
кроме, быть может, самой точки а.
Опр.
Число А называется пределом функции
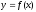 приx,
стремящемся к а,
если для любого
приx,
стремящемся к а,
если для любого
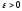 существует такое положительное число
существует такое положительное число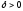 (зависящее только от
(зависящее только от ),
что при всехx,
не равных а
и удовлетворяющих условию
),
что при всехx,
не равных а
и удовлетворяющих условию
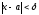 выполняется неравенство
выполняется неравенство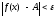
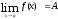 .
.
Замечание 1. Определение предела не требует существования функции в самой точке а.
Замечание
2. Если при стремлении x
к а
переменная x
принимает лишь значения, меньшие а,
или, наоборот, большие а,
и при этом функция стремится к некоторому
числу А, то говорят об односторонних
пределах функции соответственно слева
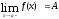 и справа
и справа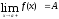 .
.
Функция имеет в точке а предел тогда и только тогда, когда в этой точке существует левый и правый предел и они равны. В таком случае предел функции равен односторонним пределам.
21. Основные теоремы о пределах. Признаки существования пределов.
