чм

FT f1, f2, q

где q - степень значимости.

8. Сравнивают Fр и FT и делают вывод. Уравнение регрессии имеет смысл при условии Fp > FT. Чем больше Fp превышает FT, тем эффективнее уравнение регрессии.

Значение критерия Фишера

Повторных опытов нет. Проверяем оценку качества аппроксимации полученных данных принятому математическому описанию.

Математическое ожидание yo = 1.2

Дисперсия относительно среднего sy=( (yo-1.2)2)/4= 1.7 Остаточная дисперсия sост=( (yo- yм)2)/3= 0.1333 Расчетный критерий Фишера Fр= 1.7/ 0.1333 = 12.6

Табличный критерий Фишера Fт= 9.1 (число степеней свободы числителя 4, знаменателя 3 в таблице 3.2) Поскольку Fp > FT уравнение регрессии можно использовать.

Результаты обработки данных в пакете Matlab 6.1 показан на рисунке 3.8

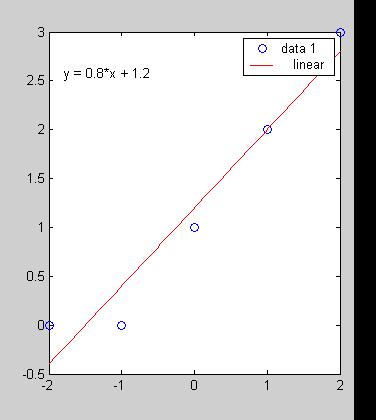
Рис. 3.8 Фрагмент окна в пакете Matlab 6.1

Тема 4.2. Имитационное моделирование на метауровне

§ 4.2.1. Методы и алгоритмы генерирования случайных величин

При имитационном моделировании на метауровне необходимо использоывать выборки случайных величин для представления параметров систем в различные моменты времени.

Рассмотрим некоторые процедуры генерации случайных величин (СВ) по заданному закону распределения.

Принципиально возможны три метода получения последовательности СВ по заданному закону распределения: аппаратный, табличный и алгоритмический.

Аппаратный использует свойство некоторых физических процессов генерировать случайные процессы (флюктуация тока в электрической цепи, излучение радиоактивного источника). Эти сигналы усиливаются, обрабатываются и превращаются в цифровую форму.

При табличном в память ЭВМ заносится таблица случайных чисел, которую можно найти в литературе по математической статистике.

Алгоритмический заключается в генерировании случайных величин по определенному алгоритму. Рассмотрим этот метод более детально.

Алгоритмический метод использует для формирования выборок СВ математические методы для получения случайных чисел имеющих равномерный закон распределения .

Фактические числа, получаемые таким способом, являются псевдослучайными, потому что возможно повторное использование алгоритма и получение снова такой же последовательности. Одним из наиболее простых и первых использовавшихся алгоритмов был алгоритм срединных квадратов. Предложенный Фон Нейманом и Метронолисом в 1946 г.

В нем каждое новое число последовательности получается взятием средних M цифр из числа полученного возведением в квадрат начального m-значного числа.

Последовательные случайные числа должны быть независимыми одно от другого (не коррелированны).

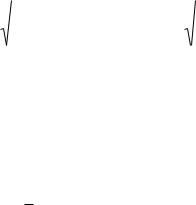
Известны рекуррентные, мультипликативные и аддитивные алгоритмы. Хорошие выборки случайных чисел дает такой рекуррентный алгоритм:

где M, D - целые числа.

Алгоритм вырабатывает случайные целые числа между 1 и D-1. Хорошую последовательность дают значение M = 8192 и D = 671101323.

В алгоритмическом языке Бейсик есть арифметическая функция RND(X), которая в зависимости от значения X, настраивает датчик случайных чисел. При моделировании можно использовать команду

RANDOMIZE(n).

Мультипликативный алгоритм:

Ri+1 = aRi(modm), где

a= 8T± 3, T- любое целое положительное число. В качестве случайного начального числа берется любое положительное число меньшее 1.

Аддитивный алгоритм Ri+1 = (Ri + Ri-1)(modm), где два случайных числа можно получить по мультипликативному алгоритму.

Для получения нормального распределения можно использовать такие алгоритмы:

1-ий алгоритм:

Yi y yi

yi 2 ln xi cos 2 X i 1

yi 1 2 ln xi sin 2 X i 1

в данном алгоритме Yi - случайная величина, которая генерируется; yi - случайная величина, распределенная по нормальному закону; xi - случайная величина, распределенная по равномерному закону; - среднеквадратичное отклонение.

2-ий алгоритм:

при использовании данного алгоритма следует иметь в виду, что при S<1 случайные числа исчисляются по формулам, а при S>1 следует начинать новый цикл расчета.

3-ій алгоритм:

n xi n2

при использовании этого алгоритма необходимо знать n (n > 6) случайных чисел распределенных по равномерному закону. В литературе можно найти алгоритмы и для других видов распределения случайных величин.

§ 4.2.2. Основы теории систем массового обслуживания (СМО).

В практических задачах часто встречаются ситуации, когда с течением времени случайным образом осуществляются те или другие однородные события, например: поступление вызовов на телефонную станцию, выход из строя элемента в технической системе, и т.д.

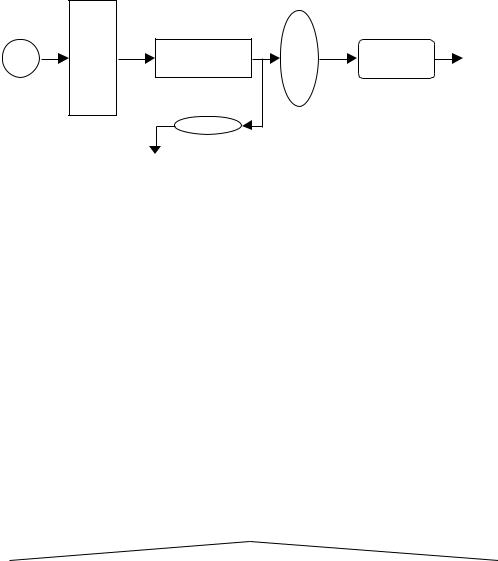
Структура такой системы может быть представлена следующей схемой:

Рис 4.1. Структура СМО

1.Источник требований;

6

2.Входной поток требований (заявок);

3.Очередь требований (ожидание обслуживания);

4.Обслуживающее устройство (m каналов);

5.Выходящий поток обработанных требований (заявок);

6.Выходящий поток не обработанных требований (заявок).

Системой массового обслуживания (СМО) называют любую систему, предназначенную для обслуживания большого потока заявок. Классификацию СМО проводят в соответствии с рис. 4.2.

Различают два основных типа СМО по условиям ожидания канала обслуживания:

СМО с отказами (заявка, которая поступила во время, когда обслуживающее устройство (ОП) занятый, получает отказ и оставляет систему)

СМО с ожиданием (заявка при отказе не оставляет систему, а становится в очередь и ждет пока освободится ОП)

Время ожидания и количество мест в очереди могут быть как ограниченными, так и неограниченными.

Система обслуживания может быть одноканальной и многоканальной.

Поступление заявки (требования) на обслуживание - случайное событие N(t). Число событий N(t) в промежутке времени (0, t) представляет собой непрерывную, неубывающую целочисленную функцию, которая увеличивается скачками.

Под потоком событий понимают последовательность случайных событий, которые происходят одно за другим в какие-то промежутки времени (различаются только моментом времени, когда они проявляются).

Такой поток можно графически представить как последовательность точек t1, t2, ...,tk на числовой оси,

- без приоритета Рис. 4.2. Классификация СМО

Рис. 4.3. Графическое представление потока

Потоком однородных случайных событий называется случайный процесс N(t) с целочисленными непрерывными значениями и непрерывным временем.

Поток называется стационарным, если вероятность попадания того или другого числа событий на участок (рис. 4.3) зависит только от длины участка и не зависит от того, где именно на вехе времени расположенный этот участок.

Поток случайных событий (ПСС) называется потоком без последствий, если число событий, которые поступили в интервалы времени которые не пересекаются, являются независимыми случайными величинами.

ПСС называют ординарным, если вероятность попадания на элементарный участок t двух или больше событий значительно меньше по сравнению с попаданием одного события.

Если - число событий в определенное время, то =1/ - плотность потока.

ПСС может быть задан распределением числа событий, которые происходят в интервале времени произвольной длины и расположенные произвольно относительно начала отсчета или распределением продолжительности интервала между отбытием событий.

Наиболее часто используемая функция распределения представляют собой вероятность того, что в интервале [0,t] или [ti, tj] состоится ровно N событий.

Если поток стационарен, ординарен и не имеет последействий, то он называется простым (стационарным пуассоновским, Пальма) потоком, т.к. распределение подчиняется закона Пуассона.

- плотность потока (среднее число событий в единицу времени); В частности вероятность того, что на промежутке не состоится ни одной события, будет:

P0 e

Поток Эрланга получают из простого путем разряжения на величину k:

f k t t k e t k!

СМО характеризуют следующими показателями: m - число каналов обслуживания;

l - длина допустимой очереди; n - число требований в очереди;

Pn - вероятность того, что в системе n требований; Pотк - вероятность отказа обслуживания;

Mоч - время ожидания;

- интенсивность обслуживания;

Tобсл - время обслуживания, распределение времени обслуживания.

Для СМО разных типов обычно ищется Pотк, время обслуживания, средняя длина очереди, число каналов обслуживания и т.д.

§ 4.2.3 Марковские модели

Если система S может находиться в En состояниях (n=0, 1, 2, 3 ...), а изменение этих состояний может происходить только в определенные моменты времени 0, 1, 2, 3, ..., i, то вероятность состояния En в момент i будет Pn(i).

Совокупность вероятностей Pn(i), соответствующая этому момента i может быть представленная вектором с числом элементов равных числу состояний:

P i P0 i , P1 i , P2 i ,

Все компоненты вектора неотъемлемые, а в сумме равняются 1. Это вектор состояния системы.

Рассмотрим случай, когда переход с одного состояния к другому зависит только от этих состояний,

0 Pn i 1. Pn i 1

n

причем каждой пари (En, En') отвечает условная вероятность P(n'\n) - система находится в состоянии En' в момент i+1, при условии, что она находилась в состоянии n в момент i.

Если Pn(0) - начальные вероятности известны, то получаем цепь Маркова. Вектор его состояния:

n

P(n'\n) - вероятность перехода от n к n'.

MP - квадратная матрица переходов, образованная из элементов P(n'\n)

n

P i 1 P i MP

Если MP зависит от времени, то цепь Маркова будет неоднородный. Множество возможных переходов может быть представлено орграфом.

Вершина - состояние. Дуга - переход.

Цепь Маркова - представление марковского процесса, который обладает тем свойством, что его состояние после момента t зависит только от его значения в этот момент и не зависит от состояния до этого момента.

Если поведение случайной функции N(t) зависит только от ее значения в данный момент времени и не зависит от "предыстории", то случайную функцию называют марковской или цепью Маркова. Случайная функция может рассматриваться как характеристика состояния некоторой технической системы.

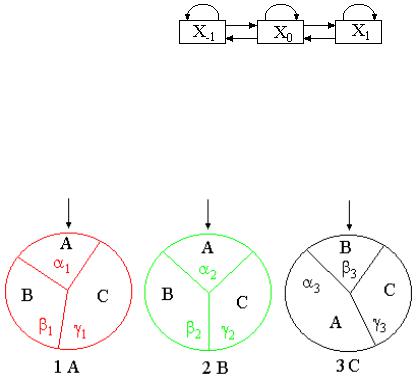
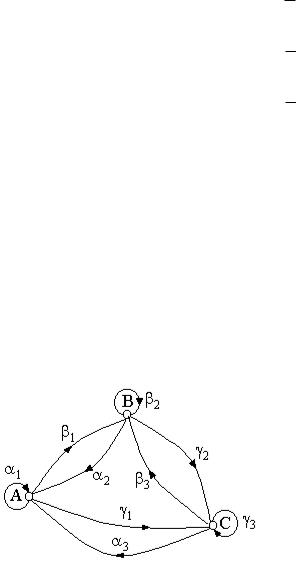
Например, цепь Маркова можно проиллюстрировать таким образом. Техническая система может находиться в трех состояниях (рис. 4.4).

Рис. 4.4. Марковская модель

X0 - все элементы системы исправные, система работает; X1 - неисправный элемент a, система ремонтируется; X-1 - неисправный элемент b, система ремонтируется.

Вероятность перехода от одного состояния в другое не зависит от вероятности возвращения обратно.

Пример:

Рис. 4.5. Формирование цепи Маркова

Испытание

1.Случайным образом выбирается номер круга, и он приводится во вращение, допуская, что вероятность остановки стрелки в определенном секторе равна величине центрального угла.

2.После остановки круга ориентируют сектор и следующим вращают круг с этим обозначением состояния системы в момент i - результат i испытание.

Начальные вероятности:

также

P1 0 13 1 2 3

P2 0 13 1 2 3

P3 0 13 1 2 3

1 1 1 1

2 2 2 1

3 3 3 1

Вероятность состояния А, В, С у любой момент i:

Рис. 4.6. Граф переходов цепи Маркова для примера

Тема 3. Методика имитационного моделирования на ЭВМ

§ 4. 3.1. Формирование замысла модели

Методика реализации имитационной модели сложной системы на ЭВМ подробно изложена в литературе (Р. Шенон Имитационное моделирование систем – искусство и наука. М.: Мир, 1978) и состоит из 3 этапов:

I — построение имитационной модели;

II — реализация модели;

III — анализ результатов моделирования

Формирование замысла модели, или этап обдумывания и планирования

1.1.Определение задачи (формулировка, процедура и график решения);

1.2.Анализ задачи;

1.3.Определение требований к информации необходимой для решения задачи;

1.4.Сбор информации (литература, документация, отчеты, консультации со специалистами, систематизация, априорные данные);

1.5.Выдвижение гипотез и принятие предложений о неизвестных сторонах задачи;

1.6.Установление основного содержания модели (реальная обстановка, задача, средства решения задачи);

1.7.Определение параметров и фазовых переменных (основные, вспомогательные, случайные, регулируемые);

1.8.Определение критериев эффективности (число, скаляр, вектор, отношение);

1.9.Определение процедуры аппроксимации (детерминированная, вероятностная, вероятных состояний);

1.10.Описание концептуальной модели в абстрактных сроках и понятиях;

1.11.Проверка достоверности концептуальной модели;

1.12.Документирование (7 позиций).

§4.3. 2. Реализация модели

1.13.Построение логической и структурной схемы (алгоритма);

1.14.Получение математических вычислений в виде, удобном для использования;

1.15.Проверка достоверности модели;

1.16.Выбор вычислительных средств (удобство программирования, затраты, достижимость);

1.17.Составление плана программы (оценка объема и затрат труда на составление программы);

1.18.Программирование (перед этим проверка структурной схемы);

1.19.Отладка программы;

1.20.Тестирование (проверка того, что программа работает по алгоритму);

1.21.Документирование (блок-схема, описание программы, листинг, сведение входных и исходных переменных, инструкции по работе с программой, оценка затрат);

1.22.Регистрация и лицензирования (верификация), валидизация (достоверность).

§4.3. 3. Результаты моделирования

3.1.Проведение расчетов по плану, контрольные расчеты, рабочие расчеты;

3.2.Принятие решения о форме и количестве итоговых результатов (таблицы, диаграммы, графики (масштабы, обозначения), промежутку вычисления);

3.3.Анализ исходной информации;

3.4.Оценка результатов (содействуют ли результаты решению поставленной задачи);

3.5.Подведение итогов;

3.6.Подготовка рекомендаций;

3.7.Документальное оформление результатов (представление научного доклада или статьи).

В 3-целому и операции:

осуществление действия;

проверка правильности действия;

документирование.

Раздел 4 Имитационное моделирование на ЭВМ.

Т.4.1. Методология имитационного моделирования.

§ 4.1.1 Имитационные и стохастические модели.

Имитационная модель – это математическая модель, на метауровне, отражающая поведение моделируемой системы при изменяющихся случайным образом во времени внешних воздействиях. Имитационная модель часто имеет алгоритмическое описание и представляется в виде программы на ЭВМ.

Алгоритм реализует функционирование системы во времени, он имитирует элементарные физические явления, составляющие процесс с сохранением логической структуры и последовательностью протекания во времени. Это позволяет получить сведения о состоянии объекта в определенные моменты времени и дает возможность оценить характеристики системы.

Имитационное моделирование используется в системах массового обслуживания (СМО) или же при моделировании систем управления, на которые воздействуют случайные процессы на макроуровне. Например, если детерминированную систему, можно описать уравнением:

Где x, y – входная и выходная переменные, t, - время, - ζ случайный параметр закон распределения, которого известен. В этом случае при изучении динамики системы решают задачу Коши с начальными условиями y(0) = ζ0 для определения траектории системы. Решением будет некоторая случайная функция φ(t). Если нужно оценить распределение y(t), а функция нелинейная, то задача становится сложной, но её можно решить методом стохастического моделирования.

Если вычислить ряд значений ξ1, ξ2, ξ3, …, ξn –, зная закон её распределения, то можно получить семейство решений уравнения Коши и обработать эти данные методом математической статистики.

Другой пример. На ТЭС и АЭС имеется много автоматических систем. Любая система во время нормальной эксплуатации может находиться в четырех состояниях: 1- исправное, 2 - неисправное, 3- ремонт, 4 – профилактика. Время нахождения в любом из состояний случайная величина. Возможны два режима эксплуатации (без профилактики и с периодической профилактикой). Нужно оценить, в каком режиме надо работать, чтобы время исправной работы было наибольшим, если будут меняться вероятность перехода из первого режима во второй, вероятность длительности ремонта и периодичности вывода системы на профилактику. В этом случае, задаваясь различными вероятностями можно оценивать возможности перехода системы из одного состояния в другое на определенном отрезке времени эксплуатации, т. е. имитировать вероятность пребывания системы в различных состояниях и решить задачу.

Стохастическое моделирование – метод получения с помощью ЭВМ статистических характеристик процессов в моделируемых системах. Для стохастического моделирования используется метод МонтеКарло. Имитационное моделирование, по существу представляет собой эксперимент на ЭВМ. Понятия стохастического и имитационного моделирования иногда отождествляют, но считается, что стохастическое моделирование – это частный случай имитационного.

ЧЯ

X Y

Рис. 4.1 Ситуация черного ящика Можно также определить, что имитационное моделирование – это оценка статистических характеристик методом ТОУ как ЧЯ с помощью ЭВМ - (рис. 4.1).

Имитационное моделирование проводится в 2 этапа:

1. Изучение объекта и получение априорной информации об объекте. 2.Построение имитационной модели.

Методика построения имитационной модели будет рассмотрена ниже.

§ 4.1.2 Математическое обеспечение имитационного моделирования.

Математическое обеспечение имитационного моделирования базируется на 3-х разделах математики (рис.

4.2).

Рис. 4.2 Структура математического обеспечения имитационного моделирования

ТВ изучает случайные события. Напомним некоторые понятия, необходимые для понимания методики стохастического моделирования. Событие – всякий факт, который в результате опыта может произойти или не произойти. их три: достоверное, невозможное и вероятное. Физический процесс, в котором осуществляется и фиксируется наличие или отсутствие событий, называется опытом. Опыт проводится при строго определенных условиях. Событие, которое в определенных условиях:

-обязательно происходит, называют достоверным;

-не может произойти, называют невозможным;

-может произойти, но и не может произойти, называют случайным.

Числовую характеристику степени возможности появления события в тех или иных условиях, которые могут повторяться неограниченное число раз, называют вероятностью. Совокупность множества однородных событий составляют первоначальный статистический материал. Различают генеральную совокупность событий N (X) и её часть N1(x), называемой выборочной совокупностью (малая выборка). Один из способов вычисления вероятности – отношение P{X} = p(x) = N1(x)/ N (X).

Для достоверных событий p(x) = 1; для невозможных p(x) = 0, а для случайных справедливо равенство

0 ≤ p(x) ≤ 1.

Количественной характеристикой некоторых событий (например, измерение физической переменной) является случайная величина, которая в результате опыта принимает одно из возможных значений, заранее неизвестное.

Математическая статистика изучает способы обработки и анализа случайных величин. По аналогии вводят понятие – частота события y*(x), представляющей собой отношение числа случаев, n(x) при которых случайная величина (СВ) x имела оно и тоже значение к общему числу случаев n..

y*(x) = n(x) / n , причем при n → ∞ y*(x) → P(x)

Вычислив частоту для разных значений y*(xi) можно построить гистограмму, график, где каждому значению xi будет соответствовать y*(xi).

В результате опыта можно получить частоту случайных значений СВ. Случайная величина может принять любое значение. Функция распределения случайной величины – плавная кривая аппроксимирующая гистограмму.

Поскольку случайные величины могут быть дискретные и непрерывные, то различают два вида

распределения Д функция распределения и U функция распределения.

F (x)

f (x) – плотность распределения

x

Рис. 4. 3 Равномерное распределение

Рис. 4.4. Нормальное распределение

Каждая случайная величина может быть охарактеризована случайными величинами: математическое ожидание, дисперсия, мода, медиана, асимметрия (скошенность), эксцесс (крутость).