
чм
.pdfОбщее выражение для закона сохранения (1.5) записано для системы координат Эйлера. Учитывая, что дивергенция вектора:
|
|
|
|
|
|
|
|
J |
|
J |
|
|
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
di |
J |
|
|
, |
|
|
|
|
|
(2.2) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
x |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
а вектор переноса субстанции J , называемый также потоком субстанции, в общем случае содержит две |
||||||||||||||||||||||||||||||||||||||||||
составляющие: конвективную I и кондуктивную (диффузионную) ( |
|
|
|
|
|
I |
|
, можно |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
J |
||||||||||||||||||||||||||||||||
|
J ), т.е. |
|
J |
|||||||||||||||||||||||||||||||||||||||
получить для каждой субстанции дифференциальное уравнение в частных производных |
( — скорость, м / |
|||||||||||||||||||||||||||||||||||||||||
с). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Например, для закона сохранения массы вещества: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Ι = ρ [кг / м -3] ,а кондуктивная составляющая определяется законом Фика. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
J = - D∙ grad C |
|
|
|
|
|
|
|
|
|
|
|
(2.3) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
где: D — коэффициент диффузии, [м2 / с]; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
С — концентрация, [кг / м –3 ] (С ρ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Если внутри объёма нет источников, генерирующих массу, то |
уравнение (2.1) |
записывается в |
||||||||||||||||||||||||||||||||||||||||
следующем виде: |
|
x |
|
|
y |
|
|
z |
|
|
|
|
c |
|
|
|
|
c |
|
|
|
|
c |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.4) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
t |
|
x |
|
|
|
|
|
y |
|
|
|
|
z |
|
|
|
x |
2 |
|
y |
2 |
|
z |
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Это дифференциальное уравнение в частных производных второго порядка.
Для закона сохранения энергии:
Ι = ρ∙е,
где: е — удельная энергия единицы массы вещества [Дж / кг]
|
|
|
|
|
|
= ρ∙е∙ +Δ |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
J |
J |
[Вт / м2] |
|
|
|
|
|
(2. 5) |
|
|
|
|
|
|||||||||||
По закону Фурье: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
J = — ∙grad T |
|
|
|
|
|
|
(2. 6) |
|
|
|
|
|
|
|||||||||
тогда уравнение сохранения энергии запишется в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
e e x e y |
e z |
|
|
|
T |
|
|
T |
|
|
T |
(2.7) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
x |
|
|
|
|
|
y |
|
|
|
z |
x |
2 |
|
y |
2 |
|
z |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При |
= const , |
ρ = const , |
|
|
e = c∙T , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где: с — удельная теплоёмкость [Дж / кг ∙ град] получается уравнение переноса тепла Фурье — Кирхгофа:

T |
|
|
|
|
x |
t |
|
|
|
|
|
|
|
|
T |
y |
T |
z |
T |
|
x |
y |
|
|||
|
|
z |
|
||
|
|
|
|
|
|
|
|
T |
|
|
|
T |
|
|
|
T |
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
a |
x2 |
|
y2 |
|
z2 |
|
(2.8) |
|||||
|
|
|
|
|
||||||||
В случае если тепло переносится в неподвижной среде = 0 и рассматривается перенос тепла только по координате х, получаем уравнение теплопроводности (Фурье) через плоскую стенку:
|
|
T |
a |
2 T |
(2.9) |
|
|
t |
x2 |
||
где: a |
— коэффициент температуропроводности, - м2/с |
|
|||
|
|
||||
c |
|
||||
Для закона сохранения количества движения (баланс сил в потоке):
Ι = ρ∙ω [кг∙м-3 ∙ м∙с-1] , по аналогии
J = — ν ∙grad ω (2.10)
Поскольку вектор, необходимо записать уравнение для каждой координаты. Например, для координаты x при постоянной плотности ρ, где g – ускорение силы тяжести, а dp/ dx – градиент давления по координате x, ν – коэффициент кинематической вязкости - м2/с
x |
x |
x |
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
p |
|
|
|
|
2 |
x |
|
|
|
2 |
x |
|
|
|
2 |
x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
z |
|
|
|
|
) g x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
t |
x |
|
y |
|
z |
x |
|
x |
2 |
|
|
y |
2 |
|
|
|
z |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
y |
|
|
|
y |
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
p |
|
|
|
2 |
y |
|
|
|
2 |
y |
|
|
|
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
(2.11) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
t |
|
x x |
|
y y |
z |
|
z |
|
y |
y |
|
x 2 |
|
|
y 2 |
|
z 2 |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
z |
|
|
|
z |
|
|
|
|
z |
|
|
|
|
|
|
p |
|
|
|
|
2 |
z |
|
|
|
|
2 |
z |
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
z |
|
|
|
|
|
) g z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||
|
|
|
t |
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
z |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Два других уравнения по координатам y, z получаются, если заменить соответствующие индексы в уравнении для координаты x .
Уравнения 2.4, 2.8, 2.11 нужно дополнить уравнением состояния
Pυ = RT |
(2.12) |
и краевыми условиями.
Краевые условия включают в себя пространственное распределение параметров (скорости, температуры, давления) в начальный момент времени (начальные условия) и законы взаимодействия между объектом и окружающей средой (граничные условия). Граничные условия представляют собой функции распределения параметров на границе и задаются несколькими способами.
Например, для параметра Т различают граничные условия первого рода:
Ts= T(x, y, z, t);
Граничные условия второго рода задаются функцией для теплового потока Q, а граничные условия третьего рода связывают температуру на границе с температурой окружающей среды через заданное значение коэффициента теплоотдачи α.
Общее аналитическое математическое описание фиксированного объёма можно записать в таком виде как систему уравнений:

|
|
di( ) |
|
|||||||||
|
t |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
e |
|
|
|
|
|
|
|
|
|||
di ( e P grad T) |
||||||||||||
|
t |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
di ( P) |
(2.13) |
|||||||||||
|
t |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
F(p, ,T) 0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T(x, y, z,t) TS (x, y, z, t), |
x, y, z S |
|||||||||||
T |
TC |
, при t 0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Это математическая модель объекта (определенного объема) на микро уровне. В уравнениях (2.12) есть переменная, P которая называется тензор давления в фиксированном объёме. Поясним значение
этого понятия. Из математики известно понятие скаляр — величина, полностью характеризуемая своим численным значением в выбранной системе единиц (температура, плотность и т.п.).
Есть и другое определение: скаляр — это тензор нулевого ранга 30 = 1.
Вектор — величина, характеризуемая в пространстве тремя величинами (три проекции на оси координат или модуль и два угла по отношению к осям координат).
Вектор — это тензор первого ранга 31 = 3.
Тензор (лат. tendo — напрягаю, растягиваю) обобщенное понятие вектора.
P ipx jp y kpz
где: i , j , k — орты;
PX , PY , PZ — векторы, составляющие тензор P по 3-м координатам.
Так как каждый вектор характеризуется тремя величинами, то тензор описывается уже 9-тью величинами, т.е. это тензор 2-го ранга 32 = 9.
|
|
PXX |
PXY |
PXZ |
|
P |
PYX |
PYY |
PYZ |
— матрица 3х3 |
|
|
|
PZX |
PZY |
PZZ |
|
Обращает внимание аналогия коэффициента теплопроводности с коэффициентом диффузии и кинематической вязкости.
§ 2. 1. 1 Методика создания математических моделей на макроуровне
На макро уровне используется укрупнённая дискретизация пространства по функциональному признаку, что приводит к представлению ММ на этом уровне в виде систем обыкновенных дифференциальных уравнений (ОДУ). Для этого приходиться вводить определенные допущения. Например, если допустить, что параметры по координатам y,z меняются мало (их производные близки к нулю), плотность среды изменяется только во времени, диффузии нет (D=0), то в этом случае математическое описание носит название — модель с сосредоточенными параметрами.
Например, покажем, как можно преобразовать исходное уравнение сохранения массы вещества на микро уровне к модели с сосредоточенными параметрами.
|
x |
|
y |
|
z |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
t |
x |
y |
z |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
c |
|
2 |
c |
2 |
|
|
|
D |
|
|
|
|
|
c |
|||
|
|
|
|
|
|
|
|||
|
x2 |
y2 |
|
z2 |
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
d |
|
x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при постоянной плотности по координате |
|
|
|
|
t |
|
x |
|
dt |
x |
|
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
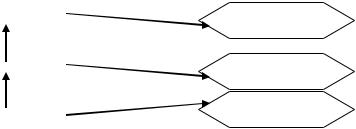
Частную производную по скорости заменим через конечные разности:
d |
|
х |
х |
|
|
х |
х |
|
|
|
вх |
вых |
|
вых |
вх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, где l длина сосредоточенного объема |
|
dt |
|
хвх хвых |
|
|
l |
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умножим обе части выражения на длину и сечение сосредоточенного объема sl=V.
d |
sl sl |
вхх |
выхх |
|
dV |
s |
вх |
s |
вых |
Mвх Mвых , где M массовый |
dt |
|
l |
dt |
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
х |
|
х |
|
расход среды.
Таким образом, ДУЧП преобразовано в ОДУ.
dV dt
Mвх Mвых , накопление массы в сосредоточенном объеме равно приходу среды минус
расход. Аналогично преобразуется уравнение энергии. Уравнение сохранения количества движения не используется, так как в сосредоточенном объеме скорость среды постоянна.
На мета уровне в качестве элементов принимают достаточно сложные совокупности объектов. Для многих ММ на мета уровне может представляться также системой ОДУ. Однако так как в этих моделях не описываются внутренние для элементов фазовые переменные, а фигурируют только фазовые переменные, относящиеся к взаимным связям элементов, то укрупнение элементов на мета уровне означает получение ММ приемлемой размерности для существенно более сложных объектов, чем на макро уровне.
Важный класс ММ на мета уровне составляют модели объектов массового обслуживания, применяемые для описания процессов функционирования информационных и вычислительных систем, которые представляются в форме алгоритма.
Структурные модели также делятся на модели различных иерархических уровней. При этом на низших иерархических уровнях преобладает использование геометрических моделей; на высших иерархических уровнях используются топологические модели.
Иерархию моделей можно представить следующей схемой (рис. 2.2).
|
Метауровень |
|
Алгоритмы |
|
|
|
ОДУ |
|
|
||
|
Макроуровень |
|
|
|
|
|
ДУЧП |
|
|
|
|
|
Микроуровень |
|
|
|
|
|
|
|
|
|
|
|
Рис.2.2 |
Иерархия математических моделей |
|
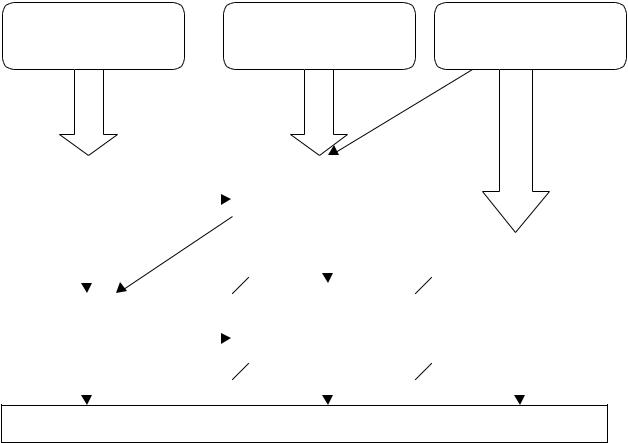
Процесс преобразований ММ относящихся к различным иерархическим уровням, для реализации на ЭВМ иллюстрирует рис. 2.3
Рис. 2.3 Преобразование математических моделей
Ветви 1 на рисунке соответствует постановка задачи, относящиеся к микро уровню, как краевой, чаще всего в виде ДУЧП. Численные методы решения ДУЧП основаны на дискретизации переменных и алгебраизации задачи. Дискретизация заключается в замене непрерывных переменных конечным множеством их значений в заданных для исследования пространственном и временном интервалах; алгебраизация — в замене произвольных алгебраическими соотношениями.
Если ДУЧП стационарное (т.е. описывает статические состояния), то дискретизация и алгебраизация преобразует ДУЧП в систему алгебраических уравнений, в общем случае нелинейных (ветвь 2).
Если ДУЧП нестационарное (т.е. описывает изменяющиеся во времени и пространстве поля переменных), то дискретизацию и алгебраизацию можно представить состоящей из 2-х этапов:
|
Микро |
|
|
|
Макро |
Мета |
||||||||
|
уровень |
|
|
|
уровень |
уровень |
||||||||
постановка |
1 |
|
|
|
|
|
|
|
|
11 |
||||
задачи |
|
|
|
10 |
|
|
||||||||
1, 8, 11 |
|
|
ДУЧП |
|
|
|
|
|
ОДУ |
|
|
|||
|
Диф. уравнения в |
3 |
|
Обыкновенные |
|
|
|
|
||||||
|
частных произ- |
|
диф. ур.; компо- |
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
водных |
|
|
|
нентные ур-ния |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Специфиче- |
|
|
|
|
|
|
4 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
9 |
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
ские модели |
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Топологические, |
|
|
|
|
||
|
Нелинейные ал- |
6 |
|
|
|
|
|
12 |
||||||
|
гебраические |
|
|
линейные, алгеб- |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
уравнения |
|
|
|
|
раические ур-ния |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
7 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
Последовательность элементарных операций на ЭВМ
1). устранение производных по пространственным координатам (ветвь 3), результат — система ОДУ; 2). устранение производных по времени (ветвь 4).
Сведение задачи решения алгебраических уравнений к последовательности элементарных операций может либо непосредственным (ветвь 5), либо через посредство предварительной линеаризации уравнений (ветвь 6), что приводит к системе линейных алгебраических уравнений.
Ветвь 8 на рис. 2.3 соответствует преобразование исходного описания задачи, относящегося к макро уровню, в систему ОДУ с известными начальными условиями. Если это система нелинейных ОДУ, то дальнейшие преобразования происходят по охарактеризованным выше ветвям 4, 6, 7 или 4, 5; если же система линейных ОДУ, то целесообразно непосредственный переход к системе СЛАУ (ветвь 9).
Для анализа объектов на мета уровне применяют либо переход к системам логических уравнений, системам массового обслуживания и т.д.
Сказанное показывает какое важное значение, отводится в математическом обеспечении моделирования численным методам решения систем различных уравнений.
Пример составления модели на макро уровне
В бак цилиндрической формы с площадью поперечного сечения F= 2 м2, поступает вода с постоянной плотностью = 1000 кг/м3. Вода из бака удаляется насосом, т.е. сток воды из бака постоянный. Составить модель объекта по каналу "расход на притоке – уровень". Мпр = 0.5 кг/с, Мст = 0.4 кг/с,
dV |
Mвх Mвых F |
dh |
Mпр Mст 2000 |
dh |
0.1 |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|||
|
dt |
|
dt |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
Это модель интегрального звена так как передаточная функция W |
(s) |
1 |
|
K |
где K=1/2000. |
|||||
F S |
|
|||||||||
|
|
|
|
|
M h |
|
|
S |
||
|
|
|
|
|
|
|
|
|||
Если расход на стоке пропорционален уровню Мст = ah, то модель будет такой:
F |
dh |
M |
|
ah 2000 |
dh |
ah M |
|
, это ОДУ первого порядка (инерционное звено |
|
пр |
|
пр |
|||||
|
dt |
|
dt |
|
||||
|
|
|
|
|
||||
первого порядка).
Более подробно моделирование ТОУ будет рассматриваться в дисциплине "Идентификация и моделирование объектов управления", которая изучается в первом семестре 4 курса.
Вопросы:
1.На какие уровни по иерархии подразделяются концептуальные ММ?
2.В какой форме представляют математические модели на макро, микро и метауровне?
3.Какие системы координат используются для записи закона сохранения? Чем они отличаются?
4.Какие составляющие входят в выражение законов сохранения субстанции?
РАЗДЕЛ 2 Методы построения и формы представление аналитических математических моделей
ТЕМА 2.2 Формальный метод построения математических моделей на макроуровне.
§- 2.2.1. Базовые элементы формальных моделей и их описание Учебные элементы:
1.Физическая величина.
2.Типы фазовых переменных.
3.Базовый элемент.
4.Компонентное уравнение базового элемента.
5.Топологические уравнения.
6.Виды топологических уравнений.
7.Аналогия компонентных и топологических уравнений.
8.Критическая протяженность объекта.
9.Источники потока субстанции и их виды.
10.Графическое обозначение базовых элементов.
11.Эквивалентная схема макро модели.
12.Процедура получения макро модели.
Использование ММ объекта в форме дифференциальных уравнений в частных производных возможно только для очень простых технических систем. Поэтому при моделировании на макро уровне в технической системе выделяются достаточно крупные элементы, которые в дальнейшем рассматриваются как неделимое целое. Непрерывной независимой переменной остаётся (в сравнении с моделированием на микро уровне) только время. Математической моделью системы на макро уровне будет система обыкновенных дифференциальных уравнений (ОДУ).
Поведение большинства технических подсистем можно охарактеризовать с помощью фазовых переменных.
Фазовая переменная — величина, характеризующая физическое или информационное состояние моделируемого объекта.
Целесообразно вспомнить понятие величины (физической величины), через которое определяется фазовая переменная (ФП).
Величина (физическая величина) — характеристика объектов или явлений материального мира, качественно общая множеству объектов или явлений, но количественно индивидуальное для каждого из них.
Физическая величина представляет собой либо обобщённое понятие (длина, масса, площадь и т.п.), либо индивидуальную характеристику конкретного объекта (сопротивление резистора R=5 МОм, ёмкость конденсатора С=5 мF).
Значение конкретной физической величины (её количественное выражение) — представление о конкретной физической величине в виде некоторого числа принятых для неё единиц.
X = { X } [ X ] (2.1)
где: X — значение конкретной физической величины; { X } — числовое значение (отвлеченное число);
[ X ] — единица физической величины.
В отличие от ФП параметр — это величина, характеризующая некоторое свойство объекта или режим его функционирования. Технологические объекты управления, как правило, состоят из нескольких подсистем различной природы, которые характеризуются двумя типами фазовых переменных: поток I и потенциал U. Фазовые переменные образуют вектор неизвестных в ММ технической системы. Вид фазовой переменной зависит от физической природы системы (таблица 2.1).
Таблица 2.1
Физическая природа системы |
|
Потенциал |
|
Поток |
|||
Механическая поступательная |
Скорость - |
v |
|
м/с |
Сила - |
F |
Н |
Пневмогидравлическая |
Давление - |
P |
|
Па |
Расход - |
M |
кг/с |
Тепловая |
Температура - |
T |
0К |
Тепловой поток - |
Q ВТ |
||
Электрическая |
Напряжение - |
U |
В |
Ток - |
|
I А |
|
Законы функционирования элемента (компонента) подсистемы задаются компонентными уравнениями, связывающими, как правило, разнородные фазовые переменные, относящиеся к данному элементу, т.е. компонентные уравнения связывают переменные типа поток и потенциал. Для простых элементов электрической природы компонентные уравнения имеют следующий вид:
U a I ; |
I a |
dU |
|
; |
U a |
dI |
|
, (2.2) |
||
|
|
|||||||||
|
|
|
dt |
|
|
|
|
dt |
|
|
где: а — параметр элемента; |
|
|
|
|
|
|
|
|
|
|
I — фазовая переменная типа поток; |
|
|
|
|
|
|
|
|||
U — фазовая переменная типа потенциал. |
|
|
|
|
|
|
|
|||
Для сложных объектов компонентные уравнения можно записать в виде: |
|
|||||||||
dV |
|
|
|
|
|
|
|
|
|
|
|
|
, V , t |
0 |
|
|
|
|
(2.3) |
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
где: V = (U , W) — вектор фазовых переменных;
U — под вектор фазовых переменных, характеризующих запасы энергии в элементах объекта; t — время;
W — вектор остальных фазовых переменных.
Компонентные уравнения могут быть линейными и нелинейными, алгебраическими, ОДУ или интегральными. Они получаются на основе знаний о конкретной предметной области. Для большинства элементов технических систем компонентные уравнения изучались в прикладных дисциплинах.
Компоненты уравнения получают либо теоретически, либо физическим тестированием, либо математическим моделированием на микро уровне.
Важно помнить, что между подсистемами различной физической природы существует аналогия.
В большинстве технических систем можно выделить три типа простейших (базовых, типовых) пассивных элементов:
1)элемент рассеивания (диссипации) энергии, где происходит преобразование любой энергии в тепловую. Это элемент типа R — сопротивление для электрической подсистемы.
2)элемент накопления энергии типа “ёмкость” — С (накопление кинетической энергии).
3)элемент накопления энергии типа “упругость” — L (накопление потенциальной энергии).
|
Так для электрической системы фазовыми переменными являются: |
типа поток — ток І |
[А, |
Кл / с]; |
|||||||
типа потенциал — напряжение U [В]. |
|
|
|
|
|
|
|
|
|
|
|
|
Компонентные уравнения простейших элементов: |
|
|
|
|
||||||
|
1) уравнение для элемента сопротивление: |
I |
1 |
|
U gU , |
(2.5) |
|
|
|||
|
|
|
|
||||||||
|
|
|
R |
|
|
|
|
||||
где: |
R — электрическое сопротивление, [Ом]; |
|
|
|
|
|
|
|
|
|
|
|
g — проводимость. |
|
|
|
|
|
|
|
|
|
|
|
2) уравнение для элемента ёмкость: |
I C |
dU |
, |
(2.6) |
|
|
||||
|
|
dt |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
где: |
С — электрическая ёмкость, [Ф]. |
|
|
|
|
|
|
|
|
|
|
|
3) уравнение для элемента индуктивность: |
U L |
dI |
|
, |
(2.7) |
|
|
|||
|
dt |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
где: |
L — электрическая индуктивность, [Гн]. |
|
|
|
|
|
|
|
|
|
|
|
Для механической поступательной системы фазовые переменные: типа поток — сила |
F , |
H , типа |
||||||||
потенциал — скорость V , м / с. |
|
|
|
|
|
|
|
|
|
|
|
|
Компонентные уравнения типовых элементов: |
|
|
|
|
|
|
|
|
|
|
1. |
F |
1 |
|
V , |
где: |
RМ |
1 |
|
; Ктр — коэффициент вязкого трения. |
|||||||||
|
|
|
Ктр |
|||||||||||||||
|
|
RM |
|
|
|
|
|
|
|
|
|
|||||||
2. |
F m a m |
dV |
|
|
, m — масса в кг — аналог электрической ёмкости. |
|||||||||||||
dt |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
Уравнение пружины F = k · x , где: x — перемещения, k — жесткость пружины: |
|||||||||||||||||
|
|
|
|
dF |
k |
dx |
k V ; |
V Lм |
dF |
, |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
dt |
|
|
dt |
|
|
|
|
|
dt |
|||||
где: |
Lм |
1 |
— аналог электрической индуктивности. |
|||||||||||||||
|
||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||
Кроме пассивных выделяют активные базовые элементы - источники
Более подробно фазовые переменные и компонентные уравнения простых элементов этих систем (кроме механической упругой) приведены в литературе. [Системы автоматизированного проектирования в 9-ти кн. Кн. 4. Математические модели технических объектов: Учебное пособие для втузов/ В.А. Трудоношин, Н.В Пивоварова; под ред. И.П. Норенкова. – М.: Высш. шк. ,1986.]
Вопросы:
6.Как определяется физическая величина?
7.Какие типы фазовых переменных используют при создании макро модели?
8.Каким образом задаётся закон функционирования элемента (компонента)?
9.Как можно получить компонентное уравнение?
§ 2.2.2. Описание связей между элементами одной природы
Связь между однородными фазовыми переменными, относящимися к разным элементам подсистемы, задаётся топологическими уравнениями, полученными на основании сведений о структуре подсистемы.
Топологические уравнения — уравнения, связывающие однотипные фазовые переменные различных элементов объекта и отражающие топологию взаимосвязей его элементов. Общий вид топологических уравнений (ТУ):
F2 (V) = 0 |
(2.8) |
ТУ выражают действие законов сохранения субстанции (вещество, энергия, количество движения), условия равновесия сил, неразрывности потоков и т.д.
Рассмотрим топологические уравнения для электрической подсистемы.
Уравнение равновесия (Первый закон Кирхгофа): |
|
Ik 0 |
(2.9) |
k p |
|
где: Ik — ток k-той ветви;
р — множество номеров ветвей инцидентных (прилегающих) к этому узлу.
Уравнение непрерывности (Второй закон Кирхгофа):

Uj 0 |
(2.10) |
j q |
|
где: j — номер ветви;
q — множество номеров ветвей, входящих в рассматриваемый контур.
Топологические уравнения строго справедливы для установившихся режимов, но их можно применять и в тех случаях, когда временем распространения возбуждения по линиям связи можно пренебречь.
Время распространения возбуждения зависит от физической природы подсистемы, т.е. от скорости распространения возмущений в соответствующей среде и размеров этой среды в конкретном объекте. Под возбуждением понимается изменение фазовых переменных.
Критической длиной кр называют приближенный предельный размер среды, при превышении которого необходимо учитывать время распространения возмущений. Оценить кр можно по формуле:
кр = Δt · υ ,
где: υ — скорость распространения возбуждения в среде, например для электрической подсистемы это скорость света 3·108 м / с ;
Δt — интервал времени, характеризующий временную точность рассмотрения процессов.
Если моделируется электрический объект в нано секундном диапазоне: Δt = 10 –9 с, то критическая длина будет 0.3 м.
Приведенные выше типовые элементы — линейные, однако, элементы подсистем могут быть и нелинейными, зависящими от режима работы.
Если к набору типовых линейных и нелинейных элементов добавить зависимые и независимые источники типа источник потока I и источник потенциала Е, то получится база двухполюсников, на основе которых можно получать математические макромодели практически любых технических объектов. Различают источники двух типов: независимые и зависимые. Уравнения источников: E = f(Z), I= f(Z), где Z время, константа или фазовая переменная.
Независимые источники используются для моделирования постоянных воздействий на объект, например, сила тяжести, может быть отражена постоянным источником силы F= mg , const.
Зависимые источники делятся на две группы:
1)источники, зависимые от времени - E = f(t);
2)источники, зависимые от фазовых переменных Q= k ΔP0.5.
Источники первой группы используются для моделирования внешних воздействий на объект. Источники, зависимые от фазовых переменных используются для отражения нелинейных свойств объекта, а также для установления взаимосвязей между подсистемами различной природы.
Для изображения простых элементов используют условные графические обозначения (рис. 2.4).
Условные графические обозначения элементов:
а) |
б) |
E |
C |
L |
I |
R |
|
|
m |
|
UP |
R |
|||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
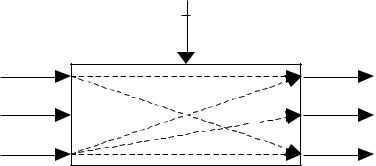
а) электрическая подсистема; |
б) механическая подсистема |
Рис. 2.4 Условные обозначения типовых элементов
Вопросы:
Какие типы топологических уравнений используют для создания макро модели? Какие типы источников субстанции используют при построении макро модели? Как представляются элементы макро модели графически?
Раздел 3 Методы построения эмпирических математических моделей
Тема 3.1. Основы методологии построения экспериментальных моделей.
§ 3.1.1. Основные понятия и определения. Классификация методов.
Специалистам по автоматизации технологических процессов требуется знание статических и динамических характеристик ТОУ. Часто для построения таких моделей используют экспериментальный метод – получение экспериментальных данных и их обработка путем решения задачи приближения функции. Результат решения – экспериментальная математическая модель (ЭММ), т.е. математическое описание определённой структуры, полученное в результате проведения эксперимента и решения задачи приближения функции.
Методологические принципы экспериментального метода:
1.Использование понятия ‘модель - чёрный ящик’.
2.Использование теории планирования эксперимента.
3.Методы проведения эксперимента.
4.Теория приближения функций.
Обобщенная параметрическая схема модели ‘чёрный ящик’ для много канального ТОУ показана на рисунке 3.1. На входе объекта вектор X ={x1,x2, …xn)- вектор входных параметров, которые в результате эксперимента можно менять и измерять. На выходе соответственно вектор выходных параметров или фазовых переменных,
|
z |
x1 |
y1 |
x2 |
y2 |
xn |
yn |
|
Рис 3.1. Параметрическая схема объекта |
которые можно измерять с определенной точностью. Вектор Z – не контролируемые случайные помехи. Методы получения ЭММ делят на два рода: экспериментальный и экспериментально-аналитический.
Экспериментальный метод имеет 3 типа: активный, пассивный, итерационный (адаптивный). Активный метод делиться на два вида: регулярный и оптимальный. Регулярный вид предусматривает
при проведении эксперимента использование контролируемых и изменяемых воздействий вектора Х, которые могут быть апериодическими и периодическими. Оптимальный отличается от регулярного тем, что воздействие производится одновременно по всем составляющим вектора Х.
