
чм
.pdf
§ 2.2.3. Описание связи между подсистемами разной природы
Учебные элементы:
1.Трансформаторная связь
2.Гираторная связь
Вбольшинстве случаев ТОУ представляю собой сочетание элементов различной физической природы. Описание связей между ними осуществляется через взаимодействие источников этих подсистем. Различают три типа связей: трансформаторная, гираторная и через зависимые параметры элементов.
Трансформаторная связь - связь между источниками разного типа и фазовых переменных одинаковой природы. В одной подсистеме p, выделяется зависимый источник потенциала - Е. Потенциал этого источника, зависит от потенциала, который создается на зависимом источнике потока І, выделяемом в другой подсистеме q.. Трансформаторная связь бывает двух видов (рис. 2.5;2.6)
p |
q |
Ip |
|
E |
I |
Uq
Ep=f1(Uq)  Iq=f2(Ip)
Iq=f2(Ip)
Рис. 2.5. I вид трансформаторной связи.
|
p |
|
|
q |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iq |
||
|
|
І |
E |
|
|
|
|
|
|
|
|||||
Up |
|
|
Eq=f1-1(Up) |
||||
|
|
||||||
|
|
Ip=f2-1(Iq) |
|
|
|||
|
|
|
|
||||
|
|
|
|
|
|
|
|
Рис. 2.6. ІІ вид трансформаторной связи. Такой тип связи характерен для электромеханических систем (реле).
Гираторная связь – это связь между источниками одного типа и фазовых переменных разной природы
(рис. 2.7;2.8)
.
|
p |
|
|
q |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ip |
|
|
|
Iq |
|||
|
|
|
E |
E |
|
|
|
|
|
|
|
|
|||||
|
|
|
Ep=f1(Iq) |
|
|
Eq=f2(Ip) |
||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Рис. 2.7. I вид гираторной связи.

|
p |
|
|
q |
||
|
|
І |
I |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
||||
Up |
|
|
Uq |
|||
|
|
Ip=f2-1(Uq) |
|
|
Iq=f1-1(Up) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
Рис. 2.8. ІІ вид гираторной связи.
Взаимодействие источников происходит таким образом: изменение фазовых сменных в одном из источников влияет на смену фазовых сменных в другой подсистеме, и через это связанные источники в разных системах. Такой тип связ характерен для гидромеханических систем (поршневой насос).
Связь через зависимые параметры элементов присуща для взаимодействия различных подсистем с тепловой системой, так как изменение температуры, как правило, приводит к изменению параметров компонентов. Так сопротивление резистора зависит от температуры.
Вопросы:
1.Чем трансформаторная связь отличается от гираторной?
Тема 2.3. Представление математических моделей на макро уровне
§- 2.3.1. Представление в форме эквивалентных схем
Структуру формальной математической модели на макроуровне можно представлять на разных уровнях абстракции. Одной из них являются эквивалентные схемы, которые состоят из набора базовых элементов и связей между ними. Методика построения эквивалентных схем содержит следующие шаги:
1.Выделить элементы, массу которых надо учесть и изобразить их условным изображением двухполюсника. Один полюс соединить с базовым узлом, определяющим инерционную систему отсчета. Второй будет соединяться с другими элементами.
2.Выделить элементы трения и упругости. Один полюс элементов трения подсоединить к базовому узлу.
3.Соединить элементы массы с элементами трения, а элементы упругости между массами.
4.Выделить источники, прикладываемые к пассивным элементам. Источник силы (потока) соединяется между базовым узлом и массой, на которую он воздействует.
Рассмотрим пример составления эквивалентной схемы для системы, состящей из элементов одной физической природы - технической
Системы механического типа, представленной на рис. 2.9а. Это грузовик массой m1 , который тянет два прицепа с массой m2, m3.
|
m1 |
|
m2 |
|
m3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а)
|
б) |
L1 |
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
R1 |
|
|
|
|
m2 |
|
|
R2 |
|
|
|
m3 |
R3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. 2.9. Механическая поступательная система (а) |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
и ее эквивалентная схема (б) |
|
|
|
|
|
|
|
|
|
||||||||
Эквивалентная схема для сил и скоростей вдоль горизонтальной оси представлена на рис. 2.9.б. |
|||||||||||||||||||||||||
Сила инерции массы автомобиля, прицепа 1 |
и прицепа 2, |
которая преодолевается силой тяги F, |
|||||||||||||||||||||||
противостоят силы сопротивления (трение об поверхность движения) |
R1, R2, R3. Упругие связи между |
||||||||||||||||||||||||
тягачом и прицепами представляются элементами L1 |
|
и L2. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если по эквивалентной схеме составить топологические уравнения, то получится система дифференционных уравнений. Это формальная математическая модель.
Для систем, в которые входят подсистемы разнообразной природы эквивалентные схемы создаются для каждой из них с учетом вида связи.
Пример такой системы и ее эквивалентная схема представленны на рис. 2.7.
Cистема состоит из гидравлической подсистемы - трубопровод, заполненный жидкостью и механической подсистемы - цилиндр с поршнем.
Гидравлическая подсистема (p) представляется тремя пассивными элементами: C1 - емкость трубопровода; L1 – индуктивность (упругость среды); R1 – сопротивление трения по длине трубопровода; и двумя активными: Р - источник давления (потенциальный); М - источник расхода (поток).
Механическая подсистема (q) состоит из следующих базовых элементов: m1 - масса поршня; m2 - масса штока; R2 - трение поршня о стенки цилиндра; R3 - трение штока об уплотнение; UP1 - упругая связь между
поршнем и штоком; F1 - (источник) сила, которая воздействует |
на поршень через шток. F2 - сила, |
||||||||
воздействующая на поршень со стороны жидкости. |
|
|
|
||||||
|
|
|
|
m |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 |
|
|
|
|
F1 |
|
|
R1L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
а)
R1 |
|
L1 |
|
UP1 |
1 |
2 |
3 |
4 |
5 |
P |
|
M F1 |
|
F2 |
|
|
C1 |
m1 R2 |
m2 R3 |
|
|
6 |
|
|
б)
Рис. 2.10. Гидро-механическая система (а),
ее эквивалентная схема (б)
Связь между подсистемами гираторная, так как движение поршня со скоростью V под влиянием F2 изменяет объем и появляется расход среды М. В свою очередь изменение давления Р вызывает появление силы F1 = k2P влияния давления жидкости на поршень.
M=k1V → Ip = f1(Uq)
F1 = k2 P → Iq = f21(Up), где
Р – давление (потенциал) гидравлической системы; V – скорость (потенциал) механической системы.
Более абстрактной формой модели на макроуровне являетсяеё представление на уровне графа. Вопросы:
1.Как составить эквивалентную схему макро модели?
§- 2.3.2. Представление математической модели в форме графа
Учебные элементы:
1.Граф, орграф
2.Вершина, ребро (ветвь), дуга
3.Матрица смежности
4.Матрица инцидентности
5.Части орграфа
Совокупность объектов, существенные свойства которых описываются связями между ними, могут быть представленные в форме графа.
Если объект (узел) представлять вершиной (изображается окружностью), а связь с другим объектом ребром или ветвью (линией), то получим граф.
Граф — это множество вершин V, связь между которыми определяется множеством ребер E.
Формальное представление графа G = {V,E}, где
V v1 , v2 , , v p |
, |
|
|
|
p - количество вершин |
E l1 , l2 , , lq , |
|
q - количество ребер. |
Если связь имеет направление (ориентацию), тогда такой граф имеет название ориентированного графа (орграфа), а связи называют дугами.
Для представления математических моделей, как правило, используют орграф.
На рис. 2.11 показан орграф, который имеет 5 вершин и 7 дуг
Рис. 2.11. Ориентированный граф (орграф)
Вершины и дуги такого графа находятся в определенных отношениях.
Две вершины vi и vj, принадлежащих множеству вершин V графа G = {V,E}, получили название смежных, если они являются граничными вершинами ребра lk принадлежащих множеству ребер E.
Отношение смежности на множестве вершин графа определяют представив каждое ребро как пару смежных вершин, т.е.:
lk={vi,vj}, где k = 1,2,3 ... q
vi — начальная вершина, откуда дуга выходит;
vj — конечная вершина, куда дуга входит.
Отношение смежности подается в виде матрицы [Cij]v= [p x p]. Для орграфа на рис. 2.8. матрица смежности имеет вид:
0 |
1 |
1 |
0 |
0 |
1 |
C 0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
Сij элемент матрицы равняется числу ребер, направленных от вершины vi к |
|
0 |
1 |
||
вершине vj. |
|||
0 |
0 |
Отношение инцидентности описывается матрицей A = [aij]V,E = [p x q]. |
|
0 |
0 |
Если вершина vi является концом (началом) дуги lk, то говорят, что они |
|
инцидентны. Строки матрицы A соответствуют вершинам, а столбцы |
|||
1 |
0 |
дугам. ai,j -й элемент равняется +1, если vi начальная вершина ребра lj и |
|
|
|
равняется -1, если vi конечная вершина ребра lj. Если связи нет aij = 0. |
Для приведенного выше орграфа матрица инцидентности имеет вид:
|
l1 |
l2 |
l3 |
l4 |
l5 |
l6 |
l7 |
|
|
1 |
1 0 |
0 |
0 |
0 |
1 v1 |
||
A |
0 |
1 |
1 0 |
0 |
1 0 |
v2 |
||
0 |
0 |
1 |
1 |
0 |
0 |
1 v3 |
||
|
0 |
0 |
0 |
1 |
1 0 |
0 |
v4 |
|
|
1 0 |
0 |
0 |
1 |
1 0 |
v5 |
||
При описании математических моделей используют некоторые части орграфа:
Подграф — часть графа образованная некоторыми дугами и инцидентными им вершинами.
Суграф — часть графа, образованная с исходного изъятием некоторых дуг, при сохранении всех вершин.
Последовательность сопредельных дуг графа образовывают маршрут. Если в маршруте все дуги отличные, то он называется цепью. Замкнутая цепь образовывает цикл. Простой цикл (контур) не содержит повторяющихся вершин.
Связный граф имеет маршрут через все вершины.
Деревом графа называют связный подграф который не имеет циклов. Ветвями дерева называют дуги дерева, а хордами - ветви, которые удаляются при образовании подграфа.
Примеры подграфа, суграфа и дерева для орграфа рис. 2.11 представленные на рис.2.9.
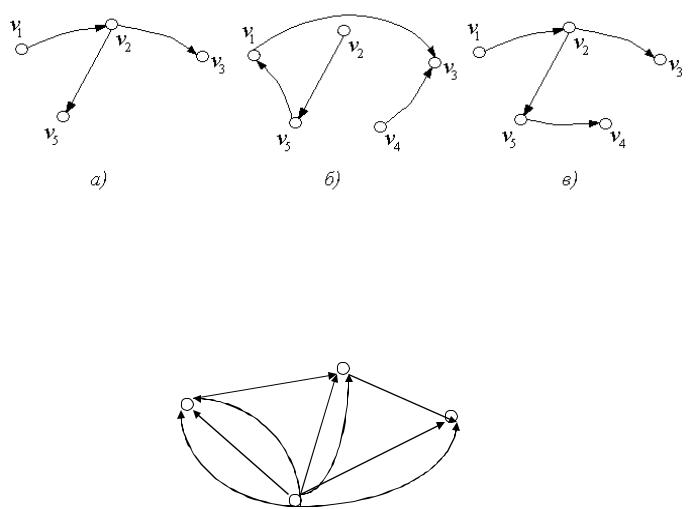
Рис.2.12. Подграф (а),
суграф (б) и дерево графа (в).
Эквивалентную схему можно представить в форме графа. Место соединения базовых компонентов заменяется узлом, а компонент дугой. Например, эквивалентную схему механической системы на рисунке 2.6б, можно представить графом (рис.2.13).
2
1
3
б
Рис. 2.13 Граф механической системы «Тягач с прицепом»
Узлом графа является точка, где соединяются два и более компонента. В базовом узле соединяются все компоненты. В узле 1 соединяются три компонента: F, m1, R1. В узле 2 соединяются четыре компонента: L1, m2, R2. В узле 3 соединяются три компонента: L2, m3, R3. таким образом модель приобрела более формальный вид.
Вопросы:
1.Чем граф отличается от орграфа?
2.Как различить маршрут, цикл, цепь, контур в графе?
3.Как получить дерево графа?
4.Чем ветвь дерева графа отличается от хорды?
5.Как закодировать граф для обработки на ЭВМ?
§ 2.3.3. Реализация аналитических математических моделей на ЭВМ
При построении ММ сложного технического объекта, состоящего из нескольких физических подсистем, нужно:
1.Провести анализ объекта моделирования;
2.Выделить в объекте однородные физические подсистемы;
3.Получить эквивалентную структурную схему для каждой из них;
4.Установить связи между подсистемами;
5.Получить математическое описание в виде системы компонентных и топологических, уравнений в следующей форме.
1). |
dU |
F (U , t) |
(2.11) |
dt |
|||
|
|
где: U — вектор переменных: состояния, моделируемого объекта размерностью n ;
F — векторфункция;
t — время (начальные условия:
2). |
Ф ( |
U0 U t 0) . Это явная форма ОДУ.
) = 0 |
(2.12) |
где: V — вектор фазовых переменных, достаточных для определения объекта, размерностью n ;
|
|
|
V dV — вектор производных фазовых переменных по времени, причём вектор V имеет только |
||
dt |
|
|
ненулевых элементов ( n); |
|
|
Ф — вектор-функция (начальные условия VO |
V |
0 ). |
|
t |
|
При составлении эквивалентной схемы следует соблюдать следующие правила. Избегать последовательного соединения источника типа I и компонента типа L, поэтому между ними нужно вставлять диссипативный элемент R. Не допустимо параллельное соединение источника типа E и компонента типа C. В этом случае последовательно с C соединяется компонент R.
Построение формальной модели на макро уровне.
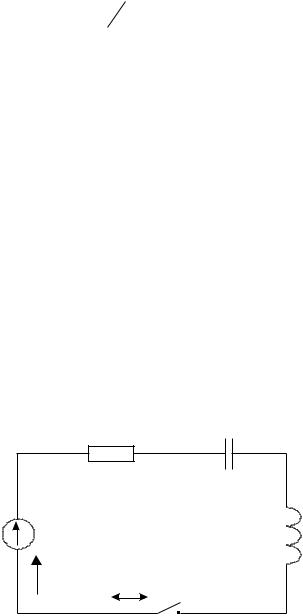
Используя описанную выше методику, составим формальную математическую модель для однородной электрической технической системы (рис. 2.14).
R |
C |
e |
L |
k
Рис. 2.3 Математическая макромодель
Система состоит из 5-ти элементов. Один активный – источник потенциала, три пассивных и один вспомогательный – ключ.
При замыкании ключа в цепи появится ток i. Первые два уравнения системы (2.13) топологические, а остальные компонентные.

|
|
|
|
|
|
|
|
iR iL iC |
|
|
|
||||
|
|
|
|
|
|
|
|
|
uR uC |
e(t) |
|||||
uL |
|||||||
|
|
diL |
|
|
duC |
|
|
uL L |
;iC C |
iL |
|||||
|
|
||||||
|
|
dt |
|
dt |
|||
|
|
|
|||||
Продифференцируем уравнение для тока через ёмкость:
C |
d2 uC |
|
di C |
|
di L |
|
dt 2 |
dt |
dt |
||||
|
|
|
Тогда с учётом того, что:
L didtL R iL uC e(t)
d2 uC |
|
1 |
( |
R |
iL |
1 |
uC |
1 |
e(t)) |
|
dt 2 |
C |
L |
L |
L |
||||||
|
|
|
|
|
или
|
d2 uC |
|
1 |
|||
|
|
dt |
2 |
C |
||
|
|
|
||||
|
|
|
|
|
||
d2 uC |
|
R du C |
||||
dt |
2 |
L dt |
||||
|
||||||
|
|
|
|
|
||
( RL CdudtC L1 uC L1 e(t))LC1 uC LC1 e(t)
(2.13)
(2.14)
Таким образом, математическое описание этой простой системы на макро уровне представляет собой обыкновенное дифференциальное уравнение (ОДУ) второго порядка, которое легко решается с помощью пакета MatLab.
На метауровне моделируют сложные технические объекты - системы управления (СУ), системы массового обслуживания (СМО). Подходы к ним различные, поэтому моделирование СМО рассмотрено в разделе 3.
Модели СУ, как правило, описываются системой обыкновенных дифференциальных уравнений.
Для решения задачи можно использовать программный комплекс MatLab, ПК МВТУ или SciLab.
Методика моделирования основана на установленные соответствия между компонентами исходных уравнений и блоками, реализуемыми на персональном компьютере (например, пакет Simulink, который содержится в составе пакета MatLab).
Рассмотрим простой пример. Система управления состоит из бака со свободным сливом воды и Пирегулятора, который должен поддерживать уровень в заданных границах.
Объект описывается дифференциальным уравнением:
T dydt y kx
ПИ-регулятор описывается уравнением:
|
|
|
|
|
|
|
dy |
||
dx |
||||
|
|
C0y C1 |
|
|
|
|
|||
dt |
|
dt |
||
выполнив следующие преобразования, получим систему уравнений
dy |
|
k |
x |
1 |
y |
|
||
|
|
|
|
|||||
dt |
|
T |
|
|
T |
|
||
dx |
C |
|
y C |
dy |
||||
|
|
|
||||||
dt |
|
|
|
0 |
|
|
1 dt |
|
Это система из двух дифференциальных уравнений первого порядка, которые были решены относительно производных. Производная первого уравнения представляет собой сумму двух слагаемых. Производная второго уравнения содержит тоже два слагаемых. Одно из них - производная из первого уравнения. Структурная схема составляется следующим образом. Предполагают, что y' существует. Если её продифференцировать, то можно получить y.
Эти уравнения логически представить в виде структурной схемы (рис. 2.13)
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
k |
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.13. Структурная схема метамодели СУ
Эта схема реализуется в среде Simulink набором соответствующих блоков из библиотеки.
РАЗДЕЛ 2 Методы построения и формы представление аналитических математических моделей Тема 2.1 Методика создания концептуальных аналитических моделей
§ 2. 1. 1 Методика создания математических моделей на микро уровне
Учебные элементы:
1.Микро, макро и мета уровни для концептуальных ММ.
2.Система координат для фазовых переменных.
3.Законы сохранения: массы, энергии, количества движения.
4.Модель с сосредоточенными параметрами.
Взависимости от места в иерархии описаний ММ
делятся, как относящиеся к микро, макро, и мета - уровням.
Особенностью ММ на микро уровне является отражение физических процессов, протекающих в непрерывном пространстве и времени. Типичные ММ на микро уровне — дифференциальные уравнения в частных производных (ДУЧП). В них независимыми переменными являются пространственные координаты (x, y, z) и время t.
ДУЧП представляют собой математическое выражение законов сохранения субстанции (вещества, энергии, количества движения):
I |
|
|
n |
|
div J m |
( 2.1) |
|||
t |
|
|
i |
|
|
|
|
|
|
|
1 |
|
||
В этом выражении: І — количество субстанции, аккумулируемое в единице объёма (единиц).
ед. суб.
Если V = dx∙dy∙dz, то V І |
|
|
— объёмная концентрация; |
м3 |
|
||
|
с |
||
J J ед. суб.
— вектор переноса субстанции через поверхность, окружающую выделенный объём,
м2 с
;
ед. суб.
mi — мощность источника субстанции, если он находится внутри выделенного объёма —
м3 с
.
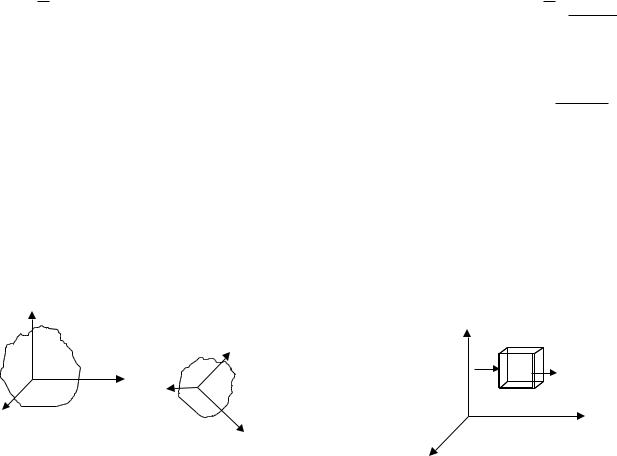
Уравнения сохранения могут быть записаны в двух фундаментально различных системах координат. Одна из них называется системой координат Лагранжа. В этой системе начало координат тесно связано с конкретной материальной частью субстанции (тело, система). При этой материальной системе перемещается и система координат, а наблюдение сосредоточено за движением материальной системы (рис. 2.1а).
Другая система координат называется системой координат Эйлера (рис 2.1б). Эта система координат фиксирована в пространстве. В данном случае, чтобы описать движение материальной субстанции фиксируется объём пространства, в который попадает и который затем покидает субстанция, т.е. в координатах Лагранжа фиксируют материальную систему, а в координатах Эйлера — объём.
В статике, когда субстанция не движется, эти системы координат совпадают.
|
Y |
|
|
|
|
|
Y |
|
Y |
|
|
|
X |
|
V = dxdydz |
|
Z |
|
|
Z |
X |
|
X |
|
а |
Z |
б |
Рис. 2.1 Система координат Лагранжа (а) и Эйлера (б)
