4. Закон Біо – Савара – Лапласа

Після дослідів Г. Ерстеда почалося інтенсивне вивчення магнітного поля постійного електричного струму. Французькі вчені Ж. Біо і Ф. Савар досліджували (1820 р.) магнітні поля, що створюються в повітрі прямолінійним струмом, коловим струмом, котушкою зі струмом тощо. На підставі численних дослідів вони встановили, що магнітна індукція поля провідника зі струмом пропорційна силі струму, залежить від форми і розмірів провідника, а також від розташування розглядуваної точки поля стосовно провідника. Наприклад, у випадку довгого прямолінійного провідника зі струмом магнітна індукція~, де − відстань від точки поля до провідника. У центрі колового витка зі струмом~, де − радіус витка.

Біо і Савар намагалися дістати загальний закон, який дав би змогу обчислити магнітну індукцію у кожній точці поля, яке створюється струмом, що тече по провіднику будь-якої форми. Однак, зробити це їм не вдавалося. На їхнє прохання за розв’язування цієї задачі взявся французький математик, астроном і фізик П Лаплас. Він враховував векторний характер магнітної індукції і висловив гіпотезу про те, що при накладанні магнітних полів справджується принцип суперпозиції, тобто принцип незалежності дії полів:

, (5.16)

де − магнітна індукція магнітного поля малого елемента провідника зі струмом, а інтегрування здійснюється по всій довжині провідника.

Лаплас додав законові Біо − Савара – Лапласа математичну форму. Така форма закону Біо − Савара – Лапласа є найзагальнішою. Магнітна індукція поля постійного електричного струму у вакуумі:

, (5.17)

де , − вектор густини струму в елементі провідника,− радіус-вектор, проведений з цього елемента у розглядувану точку поля,− коефіцієнт пропорційності, який залежить від вибору системи одиниць. У системі одиниць СІ коефіцієнт:

,

де −магнітна стала,

.

Використовуючи позначення , запишемо закон Біо − Савара – Лапласа в одиницях СІ:

, (5.18)

, (5.19)

де − кут між векторами густини струму в елементі провідника і радіусом-вектором .

Магнітна індукція поля, що створюється у вакуумі струмом , який тече по провіднику скінченної довжини і будь-якої форми, дорівнює:

. (5.20)

5. Приклади найпростіших магнітних полів провідників із струмом

1. Магнітне поле колового витка зі струмом

а) Поле у центрі витка

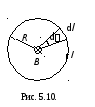Згідно з законом Біо − Савара – Лапласа (5.19) магнітна індукція поля малого елемента

,

оскільки . З рис. 5.10 випливає, що

.

Тоді

.

Після інтегрування дістанемо вираз для магнітної індукції у центрі витка:

. (5.23)

б) Поле на осі витка

Визначмо магнітну індукцію поля витка зі струмом у довільній точці А на осі витка, тобто на осі, яка проходить через центр витка перпендикулярно його площині. На рис. 5.11 зображено коловий виток радіуса R, площина якого перпендикулярна площині рисунка, а вісь лежить у цій площині.

У точці А магнітна індукція поля малого елемента

, (5.24)

оскільки .

З міркувань симетрії , оскільки сума проекцій векторіві для полів двох діаметрально протилежних елементів витка дорівнює нулеві (див. рис. 5. 11). Тобто вектор напрямлений вздовж осіу. З рис. 5.11 випливає, що

, (5.25)

, (5.26)

. (5.27)

Після підстановки виразів (5.25), (5.26) і (5.27) у формулу (5.24) знайдемо

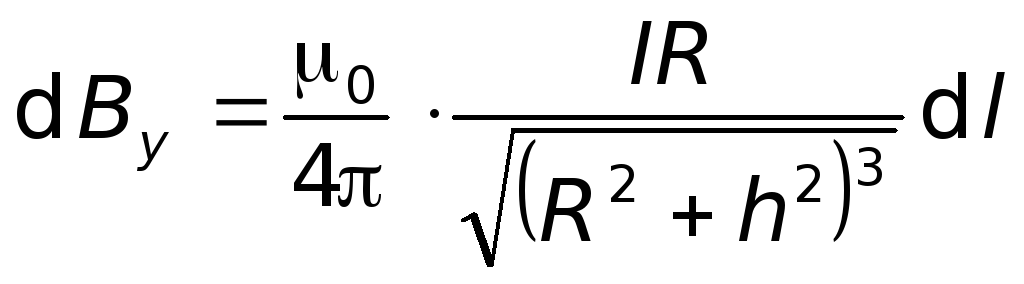. (5.28)

Після інтегрування рівняння (5.28) дістанемо магнітну індукцію поля витка зі струмом у довільній точці А на осі витка:

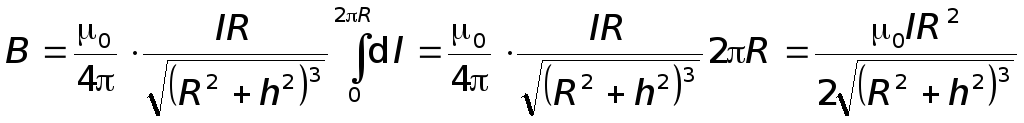. (5.29)

При

.

Одержаний вираз збігається з формулою (5.23).

2. Магнітне поле прямолінійного провідника зі струмом

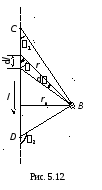Розгляньмо відрізок CD прямого провідника зі струмом I (рис. 5.12). Магнітна індукція поля, що створюється елементом згідно з (5.19)

,

де (див. рис. 5.12). Виключившиі, дістанемо:

.

Шукана магнітна індукція всього відрізка CD:

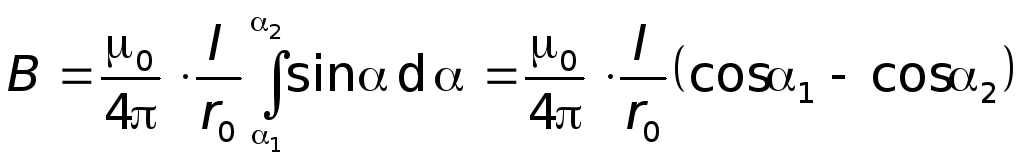. (5.30)

Для нескінченого провідника :

. (5.31)

3. Для нескінченно довгого соленоїда:

, (5.32)

де n – кількість витків, що припадає на одиницю довжини (для тороїда – на одиницю довжини середньої лінії тороїда).