Методические указания к выполнению лабораторных ра (1)

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия связи им. А.С. Попова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

∑( X (i) −

.pdf

Скачиваний:

Добавлен:

10.02.2016

Размер:

806.6 Кб

Скачать

☆

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

2.3 Для часто встречающихся процессов известны аналитические выражения функций р(x) и F(x). Так, у нормального (гауссовского) процесса (например, флуктуационной помехи) плотность вероятности записывается

p(x) =

− ( x − a)2

2σ2

(3)

2πσ

где

a =

– среднее значение или математическое ожидание случайного

X (t)

процесса

a =

∞

∫ x p(x)dx ;

(4)

−∞

σ –

среднее квадратическое отклонение случайного процесса, оно определяется

как σ =

D[X (t)]

, где D[X(t)] – дисперсия случайного процесса –

среднее зна-

чение квадрата отклонений значений случайного процесса от его среднего значения

				∞
				D[X (t )]= ∫ (x − a)2 p(x)dx .			(5)
				−∞
Функция распределения вероятностей нормального процесса записывает-
ся в разных учебниках и пособиях одним из следующих выражений:
				F (x) = 1 − Q	x − a	,	(6)
				F (x) = 1 − Q		,	(6)
					σ
					σ
где Q(z) =	1	∞	t 2
		∫ exp −		dt – гауссовская Q-функция (одна из форм интеграла
		∫ exp −		dt – гауссовская Q-функция (одна из форм интеграла
	2π z		2

вероятностей).

На рис. 1, а приведены графики гауссовского распределения вероятностей при а = 1 и σ = 0,5.

					2
1
				F(x)
0,5					1
0,5				p(x)
				p(x)
– 1	0	1	2	х	3
		а

				1
								F(x)
	p(x)			0,5
	p(x)	F(x)						p(x)
		F(x)
– 2	0	x	2	– 1	0	1	2	x 3
	б					в

Рисунок 1 – Распределения вероятностей: а – гауссовское распределение; б – распределение гармонического колебания; в – равномерное распределение

2.4

Распределение

вероятностей

гармонического

колебания

X(t) = A×cos(2πf t + ϕ), где А і f – постоянные величины, a ϕ –

случайная величи-

на, описывается выражениями:

≤ A,

0,5

arcsin

p(x) =

F (x) =

(7)

− x

> A;

> A.

Среднее значение гармонического колебания равняется 0, а среднее квад-

ратическое отклонение равняется A / 2 . На рис. 1, б приведены графики распределения вероятностей гармоничного колебания при А = 2. Когда х = А, значение плотности вероятности стремится в ∞.

2.5 Встречаются также процессы с равномерным распределением на интервале (xmin, xmax). Распределение описывается выражениями


	1	, xmin < x ≤ xmax ,		x − xmin			, xmin < x ≤ xmax ,

	− xmin								(8)
p(x) = xmax				F (x) = xmax	− xmin
	0,	x ≤ xmin , x > xmax ;			0, x ≤ xmin ,			x > xmax .

Среднее значение процесса с равномерным распределением равняется
(xmin + xmax)/2,	а	среднее	квадратическое			отклонение		равняется

(xmax − xmin ) / 12 . Графики равномерного распределения вероятностей при xmin = 0 и xmax = 2 приведены на рис. 1, в.

3 Ключевые вопросы

3.1Какие процессы называются стационарными, эргодическими?

3.2Дать определение одномерной функции распределения вероятностей случайного процесса и доказать ее свойства.

3.3Дать определение одномерной плотности вероятности случайного процесса и доказать ее свойства.

3.4Как найти вероятность попадания значений случайного процесса в заданный интервал, пользуясь функцией распределения вероятностей или плотностью вероятности?

3.5Записать выражение для математического ожидания и дисперсии случайного процесса. Каков их физический смысл?

3.6Записать выражение для нормального распределения вероятностей и объяснить смысл величин, входящих в выражение.

3.7Объяснить вид графиков распределения вероятностей гармонического колебания со случайной фазой, флуктуационного шума и процесса с равномерным распределением.

3.8Описать принцип действия устройства для измерения функции распределения вероятностей и плотности вероятности случайного процесса.

4 Домашнее задание

4.1 Изучить разделы “ Вероятностные характеристики случайных процессов”, “ Гауссовский случайный процесс” по конспекту лекций и литературе

[1, с. 53...68; 3, с. 133...145; 4, с. 49...56] и описание лабораторного макета в разд. 6.

4.2 Выполнить расчеты и построить графики функции распределения вероятностей и плотности вероятности нормального случайного процесса со средним значением а = 0 и средним квадратическим отклонением σ = 1 + 0,1N, где N – номер Вашей бригады. Расчеты провести для диапазона значений –3 σ < x < 3σ. При отсутствии таблиц гауссовской Q-функции ее значения могут быть определенные по приближенной формуле:

Q(z) 0,65 exp[–0,44( z + 0,75)2] при z > 0; Q(z) = 1 – Q(| z|) при z < 0, Q(0) = 0,5, Q(∞) = 0.

Результаты расчетов оформить в виде таблиц и графиков. 4.3 Подготовиться к обсуждению по ключевым вопросам.

5 Лабораторное задание

5.1Ознакомиться с виртуальным макетом на рабочем месте. Для этого запустить программу 1.2 Исследование распределений вероятностей случайных процессов, используя иконку Лабораторные работы на рабочем сто-

ле, а затем папки ТЭС и Модуль 1. Изучить схему макета на дисплее компьютера, пользуясь разд. 6. Уточнить с преподавателем план выполнения лабораторного задания.

5.2Исследовать равномерное распределение вероятностей. Выбрать в меню “ Выбор процесса” пункт “ С равномерным распределением”. Установить

всоответствующих окнах значения xmin = –1 и xmax = 1, крайние значения аргумента при анализе распределений Xниж = – 2 и Xверх = 2. Зафиксировать в рабочей тетради графики функции распределения вероятностей и плотности вероятности, измеренные среднее значение и среднее квадратическое отклонение.

Повторить измерение при значениях xmin = 0 и xmax= 0,5.

5.3Исследовать гауссовское распределение вероятностей. Выбрать в меню “ Выбор процесса” пункт “ С гауссовским распределением”. Установить в

соответствующих окнах значения а и σ, заданные в домашнем задании, а значения xmin и xmax такие, что охватывают диапазон значений а ± 3σ. Зафиксировать в рабочей тетради графики функции распределения вероятностей и плотности вероятности, измеренные среднее значение и среднее квадратическое отклонение.

Повторить измерение при значении а = 1 и значении σ в два раза меньшем, чем задано в домашнем задании.

Сравнить полученные результаты с теоретическими положениями: вид функций p(x) и F(x), выполнение свойств p(x) и F(x), совпадение вымеренных среднего значения и среднего квадратического отклонения с установленными.

5.4 Исследовать распределение вероятностей гармонического коле-

бания. Выбрать в меню “ Выбор процесса” пункт “ Гармоническое колебание”.

Установить в соответствующих окнах значения амплитуды А = 1, значение час-

тоты f порядка 10...20 кГц и произвольное значение начальной фазы ϕ. Установить крайние значения аргумента при анализе распределений, которые охватывают диапазон значений ±А. Зафиксировать в рабочей тетради графики функции распределения вероятностей и плотности вероятности, измеренные среднее значение и среднее квадратическое отклонение.

Повторить измерение при амплитуде А = 0,5 и измененных значениях частоты и начальной фазы.

Сравнить полученные результаты с теоретическими положениями: вид функций p(x) и F(x), выполнение свойств p(x) и F(x), совпадение измеренных среднего значения и среднего квадратического отклонения с расчетными. Сделать вывод о независимости этих характеристик от частоты и начальной фазы колебания.

6 Описание лабораторного макета

Лабораторная работа выполняется на компьютере с использованием виртуального макета, структурную схему которого приведено на рис. 2. Макет дает возможность исследовать характеристики процессов с равномерным распределением вероятностей, с гауссовским распределением вероятностей и гармонического колебания.

Установка а, σ

Осциллограф

“ Реализация

Генератор отсчетов

процесса”

с гауссовским

распределением

Вычислитель

Индикатор “ Изме-

ренное среднее

среднего значения

значение”

Установка A, f, ϕ

Генератор отсчетов

Вычислитель

Индикатор

гармонического

СКО

“ Измеренное СКО”

колебания

Вычислитель

Дисплей

гистограммы

“ Плотность

Установка xmin, xmax

вероятности”

Генератор отсчетов	Установка Xниж, Xверх
Генератор отсчетов
с равномерным
распределением		Дисплей “ Функция
	Интегратор	Дисплей “ Функция
	Интегратор	распределения
		распределения
		вероятностей”

Рисунок 2 – Структурная схема макета

Для каждого из процессов макет реализует две основные функции:

1)Генерирование N отсчетов исследуемого процесса X(t) и вывод их на дисплей “ Реализация процесса”.

2)Расчеты на основе генерированных отсчетов значений и вывод на дис-

плей:

а) функции распределения вероятностей; б) плотности вероятности; в) среднего значения;

г) среднего квадратического отклонения (СКО).

Для каждого исследуемого процесса используется свой способ генерирования отсчетов, разные параметры процессов, которыми они задаются.

Генерирование отсчетов процесса с равномерным распределением вероятностей выполняется с помощью встроенной функции randomize. Исследова-

тель может устанавливать значение xmin и xmax.

Генерирование отсчетов процесса с гауссовским распределением вероятностей выполняется с помощью нелинейного преобразования двух массивов отсчетов с равномерным распределением вероятностей, которые вырабатываются с помощью встроенной функции randomize.

Генерирование отсчетов гармонического колебания выполняется встроенным функциональным генератором со сменными амплитудой, частотой и начальной фазой колебания.

Расчет значений функции распределения вероятностей и плотности веро-

ятности выполняется в диапазоне значений аргумента от нижнего значения xниж до верхнего значения xверх. Интервал (xниж, xверх) разбивается на М одинаковых

подинтервалов протяженностью x = (xверх – xниж)/M; рассчитывается количество отсчетов kj, попадающих в j-й подинтервал (j принимает значение от 1 до М). Частота попадания значений отсчетов в j-й подинтервал qj = kj/N. При достаточно больших значениях M и N (в макете M = 200, N = 10000) значение частоты qj дает вероятность попадания значений отсчетов в j-й подинтервал. Согласно свойству плотности вероятности р(х) (строка 1 в табл. 1) вероятность попадания значений отсчетов в i-й подинтервал qj = р(хj) x, где хj = j x. Поэтому


		k j			k j	M
		k j			k j	M
p(x j	) =			=			, j = 1, M .	(9)
p(x j	) =	N		=			, j = 1, M .	(9)
		N	x		N (xверх − xниж )

Массивы значений р(хj) и хj выводятся на дисплей “ Плотность вероятно-

сти”.

На основе свойства функции распределения вероятностей F(x), приведенной в строке 5 табл. 1, рассчитывается массив значений

j
F (x j ) = x ∑ p(xk ), j =		.	(10)
	1, M
k =1

Массивы значений F(хj) и хj выводятся на дисплей “ Функция распределения вероятностей”.

Расчет среднего значения исследуемого процесса производится по фор-

муле


					1	N
			X (i)	=	1	∑ X (i) ,		(11)
			X (i)	=		∑ X (i) ,		(11)
					N i =1
где X(i), i =		– i-й отсчет исследуемого процесса. Число						выводится на
где X(i), i =	1, N	– i-й отсчет исследуемого процесса. Число					X (i)	выводится на

дисплей “ Измеренное среднее значение”.

Расчет среднего квадратического отклонения исследуемого процесса производится по формуле

Число σ выводится на дисплей “ Измеренное СКО”.

7 Требования к отчету

7.1Название лабораторной работы.

7.2Цель работы.

7.3Результаты выполнения домашнего задания.

7.4 Структурные схемы	исследований и результаты выполнения
п. 5.2...5.4 лабораторного задания	(графики и числовые значения).

7.5Выводы по каждому пункту задачи, в которых предоставить анализ полученных результатов (проверка выполнения свойств функции распределения вероятностей и плотности вероятности, совпадение экспериментальных и теоретических данных).

7.6Дата, подпись студента, виза преподавателя с оценкой по 100балльной системе оценивания.

Лабораторная работа 1.3 КОРРЕЛЯЦИОННЫЕ ХАРАКТЕРИСТИКИ

СЛУЧАЙНЫХ ПРОЦЕССОВ И ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ 1 Цель работы

Изучение метода экспериментального определения корреляционных характеристик случайных процессов и детерминированных сигналов. Исследование связи между корреляционными функциями и спектрами случайных процессов и детерминированных сигналов.

2 Ключевые положения

2.1 Корреляционной функцией (КФ) случайного процесса X(t) называется математическое ожидание произведения значений процесса, которые он принимает в моменты времени t1 и t2:

K X (t1 , t2 ) =

X (t1 ) × X (t2 )

(1)

Значение КФ KХ(t1, t2) определяют величину статистической зависимости между значениями процесса в моменты времени t1 и t2. У стационарных процессов значения КФ зависят не от выбора t1 и t2, а от расстояния между ними t = t2 – t1, а КФ обозначается KX(t). Дальше будем рассматривать лишь стационарные процессы и считать, что они являются эргодическими. Для эргодических процессов КФ определяется

		1	T / 2
K X	(t) = lim		∫ x(t) x(t + t) dt ,	(2)

	T →∞ T		−T / 2

где x(t) – реализация процесса X(t).

2.2 Независимо от вида КФ разных процессов, для них выполняются следующие свойства:

-KX(0) = РХ, где РХ – средняя мощность процесса;

-KX(0) ³ KX(t) – когда t = 0, значение функции KX(t) максимальное;

-KX(t) = KX(– t) – функция KX(t) четная;

-KX(¥) ® X (t )2 , где X (t ) – среднее значение процесса.

2.3Чем меньшее значение KX(t) по сравнению с KX(0), тем меньше статистическая зависимость между значениями процесса, которые отдалены во вре-

мени на t. Если значение KX(t) = 0, то значения процесса X(t), которые отдалены во времени на такой интервал t, являются некоррелированными. Значение KX(t) и KX(0) легче сравнивать, если перейти к нормированной корреляционной функции

	(t) =	K X	(t)
RX				.	(3)

		K X (0)

Значение RX(0) = 1 и –1 £ RX(t) £ 1.

2.4 Часто для описания корреляционных свойств случайных процессов вместо КФ используют число – интервал корреляции tк. Интервал корреляции

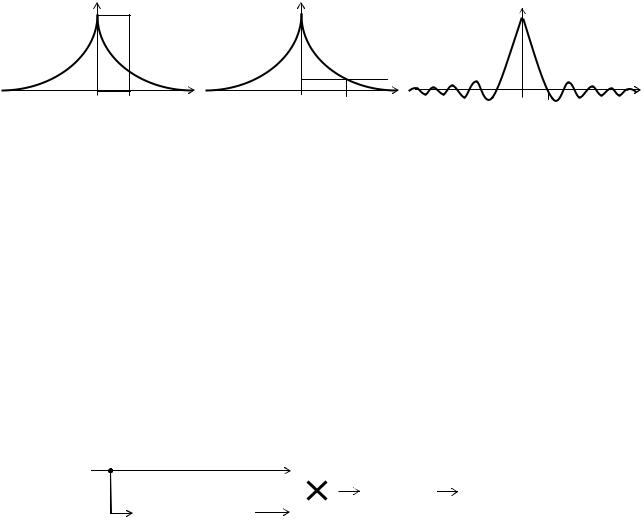
вводится для “ грубого” описания корреляционных свойств процесса, а именно, значения процесса, отдаленные на время τ > τк, считают некоррелированными, а значение процесса, отдаленные на время τ ≤ τк, считают коррелированными. Используются разные способы определения интервала корреляции:

1) Интервал корреляции τк равен основанию прямоугольника высоты KX(0), площадь которого равна площади под кривой модуля КФ (рис. 1, а):

	1		∞
τк =			∫	K X	(τ)	dτ .	(4)


	K X	(0)
	K X	(0)	0
			0

2)Интервалом корреляции является такое значение τк, что при τ > τк значение КФ не превышают некоторого заданного уровня (рис. 1, б).

3)Если КФ имеет колебательный характер, то в качестве интервала кор-

реляции τк можно принять значение τ, при котором КФ первый раз принимает нулевое значение (рис. 1, в).

KX(τ)

	τ	y	τ
τк	τ	τк	τ	τк	τ
а		б		в
	Рисунок 1 –	Определение интервала корреляции

2.5 Измерить КФ строго в соответствии с (2) невозможно, поскольку для этого необходима реализация процесса бесконечной длительности. Можно измерить КФ лишь реализации случайного процесса конечной длительности. Очевидно, чем больше длительность реализации процесса Треал, тем точнее измеренная КФ реализации отображает КФ процесса. Устройство для измерения КФ реализации называется коррелометром (рис. 2). Здесь время задержки τ определяет аргумент измеренного значения КФ. Если коррелометр, показанный на рис. 2, выполнить на процессоре или на компьютере, то можно получить массив значений КХ(kТд), где Тд – интервал дискретизации реализации процесса x(t); значение аргумента лежат в пределах – Треал ≤ kТд ≤ Треал. Полученные массивы значений kТд и КХ(kТд) выводятся на двумерный дисплей

Реализация процесса x(t) длительностью Треал

		1		Tреал	Индикатор
				∫
Устройство					значений
Устройство			Tреал		значений
задержки			Tреал	0	KX(τ)
на время τ
на время τ

Рисунок 2 –	Функциональная схема коррелометра

2.6 Основной спектральной характеристикой случайных процессов является спектральная плотность мощности GX(f), которая определяет распределе-

ние мощности процесса по частоте. Количественно функция GX(f) определяет мощность процесса в полосе частот протяженностью 1 Гц возле частоты f. Теорема Хинчина-Винера утверждает, что функции KX(t) и GX(w) связаны преобразованиям Фурье

			∞
GX (w) = 2∫ K X (t) cos(wt)dt;
			0		(5)
		1	∞		(5)
K X	(t) =	1	∫GX (w) cos(wt)dw.
K X	(t) =	p	∫GX (w) cos(wt)dw.
		p	0

Если функция GX(f) известна, то с помощью ее можно определить сред-
нюю мощность процесса
			∞	( f )df .
	PX = ∫GX			( f )df .	(6)
			0

В частности, если процесс – квазибелый шум со спектральной плотностью мощности N0 в полосе частот (0, Fmax),

PX = N0×Fmax.

(7)

GХ(f)

Fmax

Рисунок 3 – Определение ширины спектра

са:

2.7 Часто достаточно знать ширину спектра процесса Fmax. Ширина спектра случайного процесса определяется по функции GX(f) такими же методами, как и ширина спектра детерминированного сигнала. На рис. 3 показано, как ширина спектра определяется на заданном уровне y, т.е. Fmax – протяжность области частот, вне которой спектральная плотность мощности процесса не превышает значение у.

Поскольку функции KX(t) и GX(f) связаны преобразованиям Фурье, то имеется связь между шириной спектра Fmax и интервалом корреляции tк процес-

tк×Fmax = 0,5.

(8)

Знак равенства в выражении (8) следует понимать следующим чином – произведение интервала корреляции и ширины спектра процесса является величиной порядка 0,5.

2.8 Корреляционная функция является также характеристикой детерминированного сигнала, хотя и нет такого толкования, как для случайного процесса. КФ непериодического детерминированного сигнала определяется

K s (t) = T∫s s(t ) s(t + t)dt ,

(9)

где Ts – продолжительность сигнала s(t).

Измерить КФ детерминированного сигнала можно с помощью коррелометра, схема которого приведена на рис. 2. Отличия: интегрирование ведется на интервале (0, Ts) и отсутствует множитель перед интегралом.

Пусть s(t) – П-импульс амплитуды А и длительности Tим

s(t ) = A,

0 £ t < Tим ,

(10)

t < 0, t ³ Tим .

После подстановки (10) в (9) получим

K s

(t) = A2Tим (1 -

/ Tі ),

£ Tим ,

(11)

> Tим .

КФ П-импульса показана на рис. 4, а.

Из выражения (9) вытекает, что Ks(0) = Es – энергии сигнала s(t). Преобразование Фурье от Ks(t) дает квадрат амплитудного спектра (спектральную плотность энергии) сигнала s(t). Преобразование Фурье от выражения (11) дает квадрат известного выражения для амплитудного спектра П-импульса

2			sin(pfTим ) 2
S		ATим		,	- ¥ < f < ¥ .	(12)

	( f ) =
			pfTим

	Ks(τ)	2	Ks(τ)
2		0,5А Тим
2		0,5А Тим
А Тим

– Тим	0	Тим	τ	– Тим	0	Тим τ
	а				б
					б

Рисунок 4 – Корреляционные функции: а – П-импульса, б – радиоимпульса

2.9 Рассмотрим радиоимпульс длительности Tим с П-образной огибающей

s(t ) = Asin(2pf0t + j0 ),		0 £ t < Tим ,	(13)
0,	t < 0,	t ³ Tим ,

где А, f0 и j0 – амплитуда, частота и начальная фаза колебания. После подстановки (13) в (9) получим

K s

(t) = 0,5A2Tим (1 -

/Tим )cos 2pf0 ,

£ Tим ,

(14)

> Tим .

Из (14) вытекает, что КФ радиоимпульса есть косинусоида с нулевой начальной фазой и не зависит от фазы радиоимпульса. Поэтому, если начальная фаза радиоимпульса j0 является случайной величиной, то КФ радиоимпульса

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.11.2018470.53 Кб5Метод. инновации.doc
#
17.08.2019441.86 Кб9метод1.doc
#
07.05.20191.9 Mб5метода по еж_комплекс.doc
#
04.11.2018503.3 Кб2метода по Ценообразованию.doc
#
25.09.2019416.26 Кб6Методика измерений.doc
#
10.02.2016806.6 Кб26Методические указания к выполнению лабораторных ра (1).pdf
#
10.02.2016883.65 Кб31Методические указания к выполнению лабораторных ра.pdf
#
10.02.2016207.36 Кб11Методические указания по курсовой работе Политэкономия.doc
#
25.11.2019640 Кб11Методическое руководство по биометрии.doc
#
26.08.20196.22 Mб3Методичка по Круг-2000 - 2008.doc
#
24.11.2018166.4 Кб3Методичка по лаб. работе по ИРС [LZW].doc