1.9 Способы повышения верности и скорости передачи информации в системах с рос

Ранее указывалось, что искажения командных сигналов, особенно при запаздывании, вызывают значительные искажения регистрируемых сообщений. В системах с безадресным повторением характер проявления помех в обратном канале при решающей и информационной обратной связи примерно одинаков: образование сигнала и подавление сигналаприводят к необнаруживаемым ошибкам и неправильной регистрации соответственноикодо­грамм; подавление сигналаи появление сигналавызывают пропускикодограмм. В системах с адресным повторением трансформация адреса приводит к ошибке, эквивалентной подавлению кодограммы в прямом канале. Поэтому цена искажений командных сигналов в обратном канале больше, чем цена искажений рабочих кодограмм в прямом канале.

Рассмотрим некоторые особенности искажений сигналов в системах с РОС с позначной проверкой. В таких системах целесо­образно обеспечивать асимметрию алгоритма работы приемного уст­ройства, добиваясь чтобы привыполнялось неравенство. Действительно, если в качестве сигналаиспользуется одна из комбинаций-кода, то вероятности

; ,

где вероятность трансформации кодограммы в обратном канале выражена

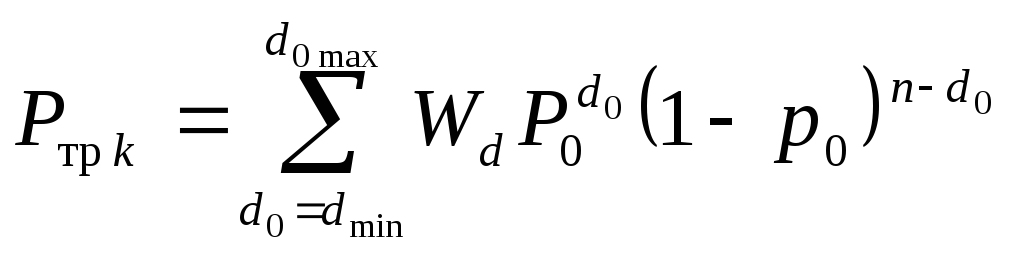, (1.53)

–число кодограмм с весом . Образование сигналаи трансформация сигналав разрешенную кодограмму вызовут ошиб­ки при регистрации сообщений с вероятностями

; .

Коэффициент

(1.54)

зависит от исправляющей способности кода и уровня шумов в ка­нале , причем с увеличениемкоэффициентвозрастает. Для каналов высокого качества со средней вероятностью искажения сим­волаи кодов сизначение. Например, при ошибке в ДКи помехоустойчивом (10,5)-коде ве­роятностьи. Случаи, когда, встречаются на практике очень редко.

Следовательно, ошибки, обусловленные образованием сигналов , преобладают над ошибками из-за подавления сигнала. Поэтому путем рационального кодирования должна быть обеспечена защита от образования ложных сигналов запроса.

Подавление сигнала вызывает на приемной станции стираниекодограмм и, так как в накопителе передающей станции эти кодограммы также стираются, исправить ошибку становится невозможным. В то же время при образовании сигналасерия изошибочно повторенных кодограмм фиксируется, и если эта серия обладает каким-то отличительным признаком, то она может быть исключена при регистрации. В результате лишь снижается средняя скорость передачи информации.

Адаптивные системы ПД с ОС с помехоустойчивыми сигналами и, обладающие асимметричным алгоритмом обработки, будем называть систе­мами с надежным командным сигналом (РОС-НКС, ИОС-НКС).

Увеличения помехоустойчивости командных сигналов можно до­стигнуть тремя методами: повышением их энергии, применением групповой проверки и использованием обратной связи с сигналами подтверждения.

Первый метод сопряжен с увеличением мощности передатчика или длительности посылок; он ухудшает энергетическую скрыт­ность связи, повышает уровень станционных помех и оказывается эффективным только в каналах с низким уровнем шумов.

При втором методе передается и проверяется раз группа кодограмм, одна из которых используется в качестве командной. В результате мажоритарной обработки вероятность ошибочного де­кодирования уменьшается. Недостаток метода заключается в том, что среднее число повторений

,

где – среднее число повторений в режиме позначной передачи, быстро

увеличивается с ростом ,и.

Наиболее эффективен метод с использованием обратной связи с сигналами подтверждения (РОС-ПС), предложенный Р. И. Зверевым и представляющий со­бой развитие метода С. Чанга. Пусть алгоритм работы систе­мы РОС-ПС таков, что принятый в обратном канале сигнал запро­са всякий раз ретранслируется по прямому каналу в виде сиг­нала, после чего кодограмма повторяется. Такой алгоритм позволяет обнаруживать ошибочно повторенные кодограммы, а при запаздывании – всепоследующих кодограмм сравнением по­следней рабочей кодограммы с предыдущей.

Предположим, что приняты без обнаруженных ошибок две последовательности кодограмм:

; (1.55)

; (1.56)

причем в последовательности (1.55) образовался ложный сигнал запроса , а в последовательности (1.56) – ложный сигнал запросав результате трансформации кодограммы. При этом ошибочно повторенная в последовательности (1.55) кодограм­мабудет исключена в результате сравнения ее с предыдущей кодограммой, а в последовательности (1.56) ошибка может быть только обнаружена. Если, однако, сигналы в накопителе передаю­щей станции сохраняются настолько долго, что искаженную кодо­грамму можно запросить повторно, то эта ошибка исправима. Для этого следует после приема сигналане фиксировать кодограм­му, а вначале послать сигнал, при этом окажется принятой последовательность, и ошибка будет устранена.

Искажения при таком алгоритме декодирования могут возник­нуть в двух случаях:

– если в обратном канале образовался сигнал , а в пря­мом канале кодограмматрансформировалась в разрешенную ко­дограмму(последовательность);

– если в прямом канале кодограмма трансформирова­лась в, а при повторной передачевновь трансформи­ровалась в(последовательность).

Вероятность таких ошибок при декодировании равна:

.

Так как

; ;,

где , – вероятности трансформации кодограмм в прямом и обратном каналах, то

.

Если , то; привероятность

и, следовательно, такие ошибки можно не учитывать.

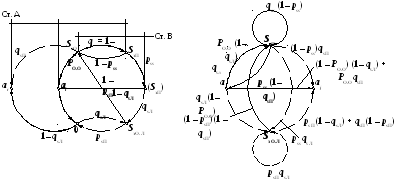
Обобщенный алгоритм работы системы с РОС-ПС. Схема вероятностных переходов системы с РОС-ПС показана на рис. 1.22, где по-прежнему в скоб­ках обозначены принятые, а без скобок – переданные сигналы.

Из рис. 1.22 видно, что возможны два пути развития процесса передачи информации:

– при передаче кодограммы ошибка не обнаруживается с вероятностью, и сигналне посылается;

– при передаче кодограммы ошибка обнаруживается с вероят­ностью, и сигналпосылается.

В первом случае при отсутствии ложного запроса ст. А передает очередную кодограмму , для которой цикл повторяется. Во втором случае сигналпосылается всякий раз при обнаружении ошибки или трансформации кодограммыв сигнал, поскольку алгоритм обеспечивает дуплексную связь с переспросом. Если сиг­нал принят правильно с вероятностью , то по прямому каналу посылается сигнал. При подавлении сигналас

вероятностью со ст. А передается очередная кодограмма. Переход из узлов графа () и () к передаче ложного запроса возможен с вероятностью.

При передаче сигнал может быть принят правильно с ве­роятностьюи, при отсутствии искажений в обратном канале, кодограммабудет повторена ст. А. Если же сигналисказится, то по обратному каналу вновь будет послан сигнали т. д. до тех пор, пока сигналне будет принят правильно. Факт безошибочного приема этого сигнала свидетельствует о нормальных условиях в обратных каналах, после чего ст. В начнет регистрировать сообщение.

Таким образом, смысл подтверждающей обратной связи заключается в том, что сигнал запроса используется в качестве зон­дирующего для определения состояния обоих каналов. Такой режим работы может оказаться эффективным при медленных замираниях, а также при кратковременных перерывах связи.

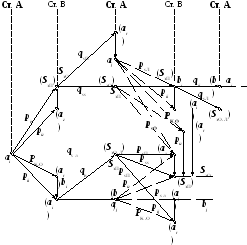
Рисунок 1.22 – Схема вероятностных переходов системы с РОС-ПС

Ложный сигнал запроса обнаруживается с вероятностью, после чего посылается запросна повторение. Если же сигналтрансформировался в одну из разрешенных кодограммс вероятностью, то возникнет ошибка типа вставки сигналов.

Вероятность ошибки. Если уровень помех в обоих каналах мал и ,,,, то нижняя граница вероятно­сти ошибки в ДК

.

Для определения точного значения составим граф си­стемы (рис. 1.23, а). Переход от узла графа () к узлу () через узел (), соответствующий появлению ошибок из-за обра­зования ложного запроса в обратном канале, содержит ветви гра­фа с малыми переходными вероятностями.

Два других перехода из () в (), соответствующие трансформации рабочей кодограммы в прямом канале и подавлению сигнала запроса, имеют только одну ветвь с малой переходной вероятностью.

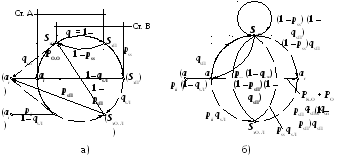
Рисунок 1.23 – Граф системы POC-ПC для определения

Поэтому в системе ПД с РОС-ПС ошибки, обусловленные неравенством , значительно меньше, чем в обычной системе РОС. Дополнительным введением асимметрии в обратном канале можно обеспечитьи сущест­венно ослабить влияние помех на верность связи.

Построим преобразованный граф (рис. 1.23, б), узлы которого отображают работу передатчика ст. А, и с его помощью най­дем матрицу переходных вероятностей, которую необходимо записать в виде

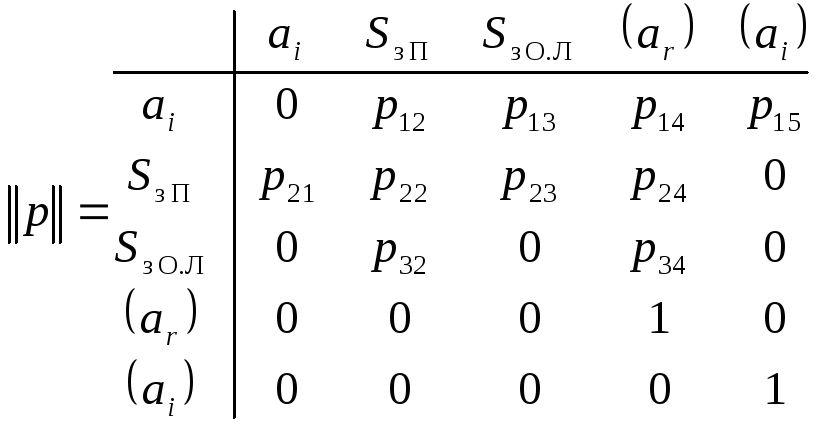, (1.57)

где

; ;;

; ;;;

; ;.

Матрица (1.57) разложима, так как узлы ,инесу­щественны, а узлы () и() – существенны. Нормальная формула матрицы имеет вид

. (1.58)

Для определения вероятности найдем алгебраиче­ские дополнения

;

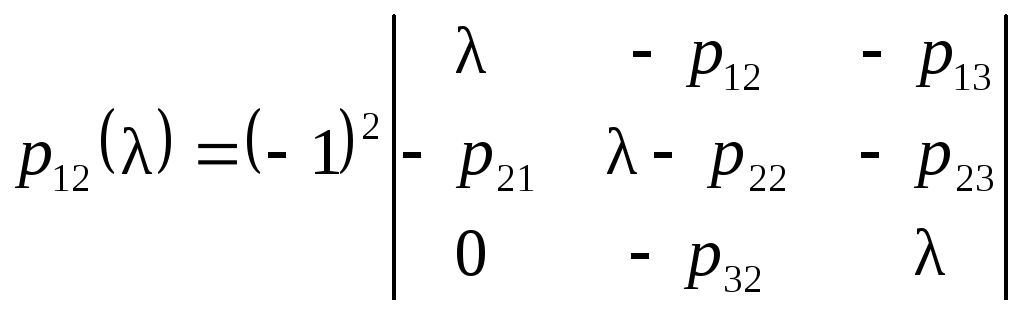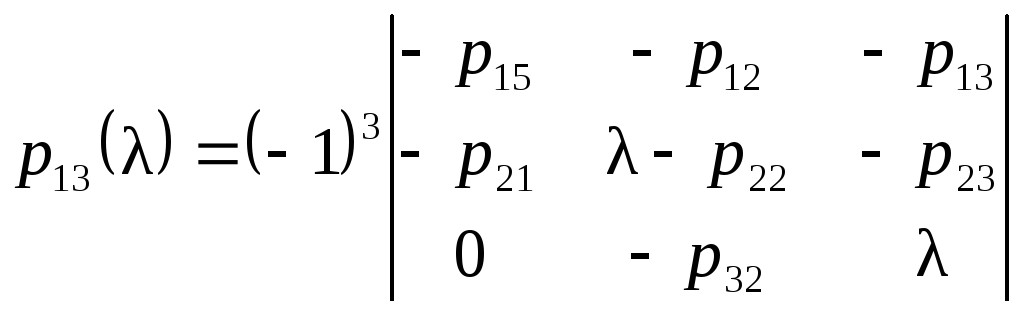
и после преобразований получим выражение для вероятности ошибки в ДК

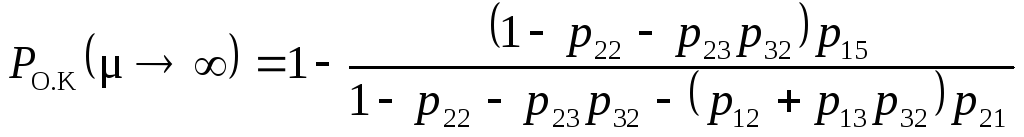. (1.59)

Выражение для вероятности можно также представить в виде

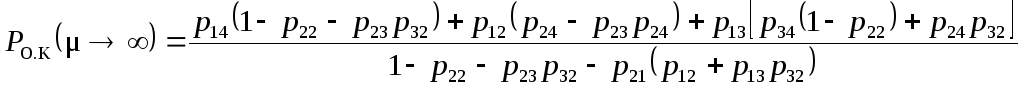. (1.60)

Эта формула менее компактна, чем (1.59), но она лучше отображает влияние переходных вероятностей на верность связи. В каналах высокого качества вероятности ,,,изна­чительно меньше, чем,,,и приближенно

. (1.61)

Анализ формул (1.59) и (1.61) показывает, что ошибки в си­стеме с РОС-ПС в основном обусловлены трансформацией рабочих ко­дограмм в прямом канале и подавлением сигнала запроса в обрат­ном канале. При идеальной обратной связи ,и вероятность ошибки в ДК

. (1.62)

Выражение (1.62), как и следовало ожидать, совпадает с (1.43), поскольку при отсутствии помех в обратном канале систе­мы с РОС и с РОС-ПС эквивалентны. В реальных каналах и, при этом вероятность ошибки в системе ПД с РОС, согласно выражению (1.42),

. (1.63)

Сравнивая формулы (1.59) и (1.63), видим, что при выполне­нии условия

система с РОС-ПС обеспечивает выигрыш в помехоустойчивости по сравнению с системой с РОС. Проанализировать это неравенство в общем виде затруднительно, так как переходные вероятности за­висят не только от уровня помех, но и от способа кодирования. Если, однако, ,,, то получим условие

. (1.64)

Так как ,,, то система с РОС-ПС всегда дает выигрыш, причем тем больший, чем больше вероятность ложных запросов и меньше вероятность необнаруживаемых ошибок в пря­мом канале. Это объясняется тем, что нагрузка обратного канала в системе с РОС-ПС несколько уменьшается за счет увеличения на­грузки в прямом канале.

Для отыскания вероятности ошибки при ограниченном числе повторений найдем переходную вероятность в матрице (1.58) за циклов:

.

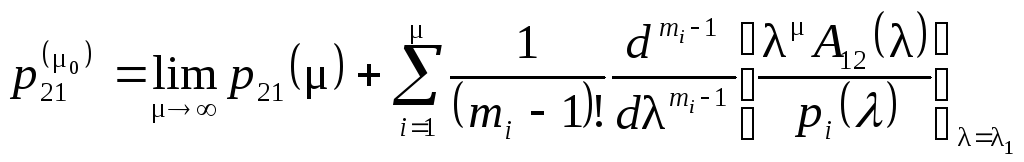Вычисляя в каждом конкретном случае корни характеристического уравнения

,

можно найти значение , а затем и вероятность, подоб­но тому, как делалось в параграфе 1.8:

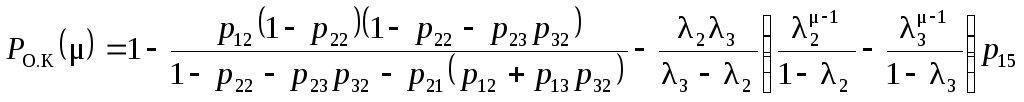, (1.65)

где корни характеристического уравнения кратности будут равны

; ;.

Среднее число повторений. Борьба с помехами в обратном ка­нале приводит в системе с РОС-ПС к увеличению среднего числа по­вторений. Из рис. 1.23, а видно, что наиболее вероятным перехо­дом от кодограммы кявляется переход через блуждающую точ­ку графа 0 с вероятностью. Возможны такие менее ве­роятные варианты переходов:

– через узел с вероятностью(обнаружение ошибки и подавлением сигнала запроса);

– через узлы ,ис вероятностью(искажение сигналав прямом канале);

– через узлы ,, (),,с вероятностью(обнаружение ошибки в прямом канале, об­разование сигнала в обратном канале и его подавление при последующем запросе);

– через узлы 0 и (образование сигналав обратном ка­нале и его

трансформация в разрешенную кодограмму в прямом ка­нале);

– через узлы 0, и(обнаружение сигналав об­ратном канале и трансформация сигнала, посылаемого после этого по обратному каналу).

Заметим, что эти варианты возможны при возвращении системы в узел через узел (). Причисло таких вариантов неограниченно. Поэтому целесообразно пользоваться графом на рис. 1.24, а, соответствующим схеме вероятностных переходов на рис. 1.22, и преобразован­ным графом рис. 1.24, б.

Матрица переходных вероятностей при этом имеет вид

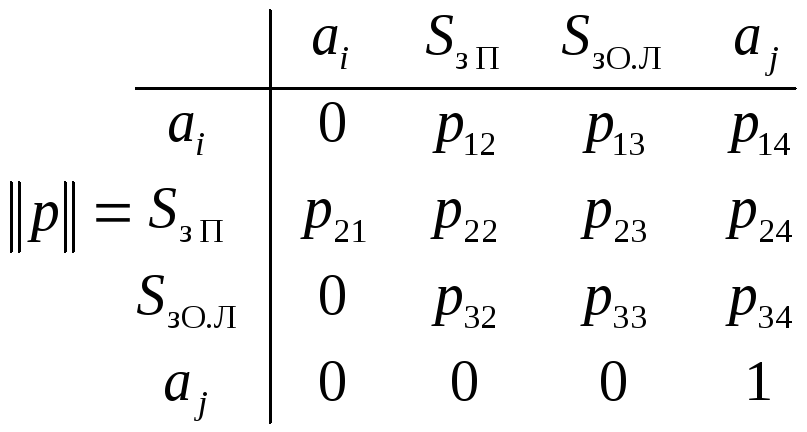, (1.66)

где

; ;;

; ;;;

; ;.

Нормальная форма матрицы (1.66) будет определяться записью

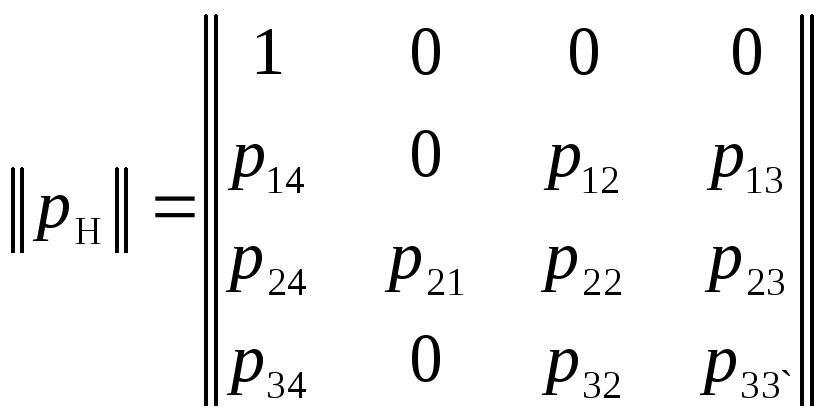. (1.67)

Для определения вероятности перехода откзациклов составим характеристический определитель матрицы (1.67):

и решим характеристическое уравнение:

.

б)

а)

Рисунок 1.24 – Граф системы РОС-ПС для определения

Если вероятности ,изначительно меньше вероятностей,,и, то получим более простое характеристическое уравнение

,

откуда получаем корни кратности .

Переходная вероятность матрицы (1.67) за циклов определяется выражением

,

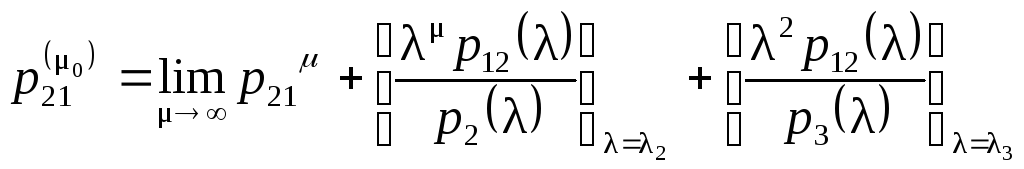где алгебраическое дополнение , аи. Так как финальная вероятность дискретной це­пи Маркова с одним стоком равна единице, то

.

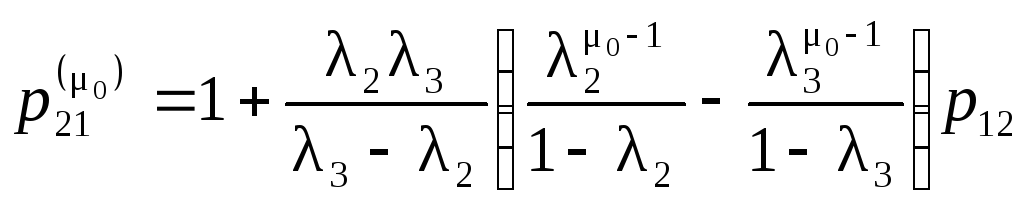Среднее число повторений сигналов, согласно формуле (1.50),

.

Так как сумма

,

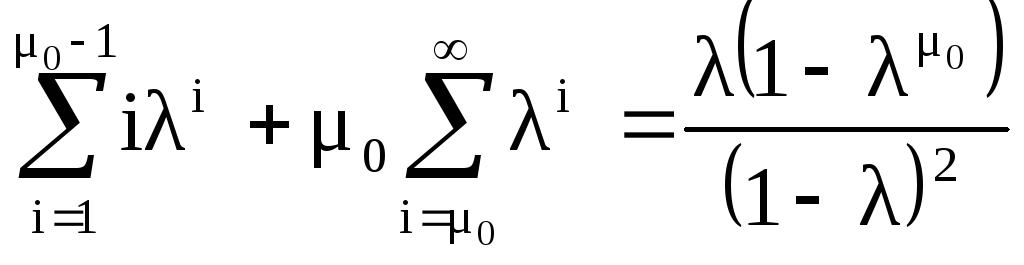то окончательно получаем

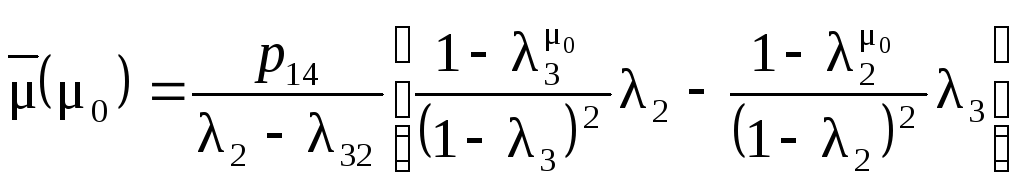. (1.68)

При неограниченном числе передач величина числа повторений сигналов будет определяться выражением

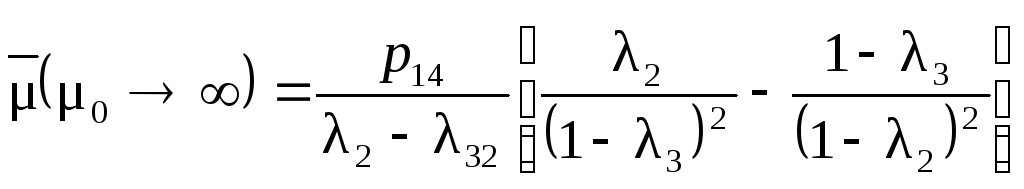. (1.69)

Приведенные выражения позволяют определять основные инфор­мационные показатели системы ПД с РОС-ПС.