Перейдем от матрицы (1.39) к более простой матрице:

. (1.41)

Из характеристического определителя этой матрицы

алгебраические дополнения при корне будути, откуда финальная вероятность

. (1.42)

Следовательно, при неограниченном числе повторений вероят­ность ошибочного приема определяется выражением

. (1.43)

Формулы (1.42) и (1.43) учитывают искажения сигналов в обо­их каналах при произвольном уровне помех.

Практически число повторений всегда ограничено некоторым значением . Характеристическое уравнениематрицы (1.41) имеет корниикратности. Тогда вероятность правильного приема зациклов можно определить через выражение:

.

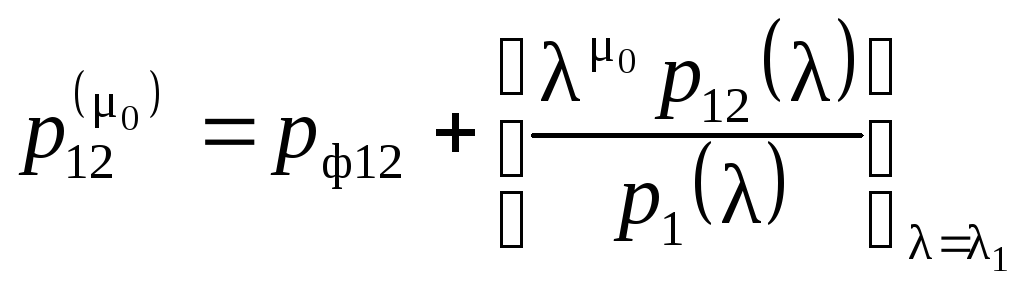Подставив значения

; ,

получим

,

откуда после преобразований вероятность ошибки при ограниченном числе повторений

. (1.44)

В этой формуле первое слагаемое характеризует вероятность ошибки за предыдущих циклов, а второе слагаемое – за последний цикл при-кратной передаче.

Заметим, что при двухальтернативном режиме работы приемного устройства алгоритм декодирования сигнала при последнем цикле повторения изменяется и область неопределенности включается в зону ошибочных решений. Это означает, что дискретная цепь Мар­кова становится неоднородной и при последней передаче матрица (1.38) изменяется. Если, однако, , то, как следует из табл. 1.4, присущественно изменятся лишь условия оши­бочного приема, а условия правильного приема сигналов практи­чески останутся прежними.

Таблица 1.4 – Условия приема

Событие	Вероятность события
Появление ошибки, исправляемой при повторении		0
Появление неисправляемой ошибки
Правильный прием сигналов

Если условие не выполняется, то следует пользовать­ся точной формулой:

,

(1.45)

получающейся из выражения (1.44) путем замены вероятности на. Из формулы (1.45) следует, что с увели­чениемвероятность ошибки уменьшается, если выражение в квад­ратных скобках больше нуля, т. е. если

или

при . (1.46)

Неравенство (1.46) представляет собой условие повышения верности связи в адаптивных системах ПД с РОСпри увеличении числа повторений сигналов и свидетельству­ет о пороговых свойствах таких систем.

Среднее число повторений. Най­дем значение , необходимое для оценки избыточности и средней ско­рости передачи информации в систе­ме ПД с РОС. При этом будем интересо­ваться вероятностью переходазациклов от передачи кодограм­мык передаче очередной кодо­граммы, независимо от наличия при этом ошибок. Из рис. 1.20, а следует, что переход отквозможен двумя спосо­бами: непосредственно через узлыII и III с вероятностями и, а также в результате возвращения к исходному состоянию с вероятно­стьюс последующим перехо­дом через узелIII с вероятностью . Цикличность рассматриваемых процессов приводит к гра­фу, показанному на рис. 1.21, а. Узлы I иIV графа связаны c ра­ботой ст. А, а узлы II и Ш – ст. В. Это позволяет по­строить преобразованный граф (рис. 1.21, б), где переходные ве­роятности

; . (1.47)

Рисунок 1.21 – Граф системы РОС для определения

Стохастическая матрица преобразованного графа

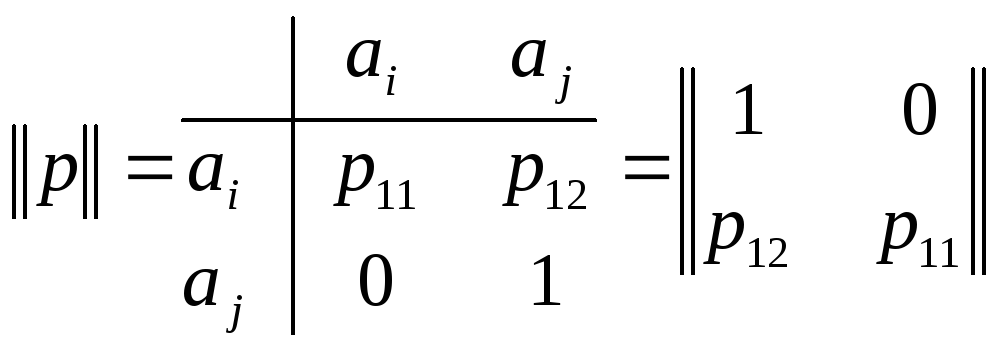. (1.48)

На основании теоремы Перрона вероятность

. (1.49)

Среднее значение числа передач при заданной величине будет

. (1.50)

Подставив выражение (1.49), после преобразований получим

. (1.51)

При идеальной обратной связи вероятности и вели­чина

. (1.52)

Формулы (1.43), (1.44), (1.49) и (1.52) были получены в предположении, что запаздыванием сигналов можно пренебречь. Данные выражения пригодны только для практических расчетов, когда величина мала.