1.8 Анализ адаптивных систем с рос без запаздывания сигналов

Для иллюстрации описанной методики рассмотрим вначале простейший случай, когда ошибки в адаптивной системе ПД с РОС статистически независимы, запаздыванием сигналов можно пренебречь, и определим зависимости и.

Вероятность ошибки. На рис. 1.19 изображена схема вероятностных переходов, где принимаемые сигналы показаны в скобках.

Анализируя работу системы, можно выделить на схеме три характерных состояния:

– состояние I: со ст. А передан сигнал ;

– состояние II: на ст. В принята запрещенная кодограм­ма

(вероятность ) или сигнал(вероятность); при этом ошибка обнаруживается с вероятностьюи по обратному каналу посылается сигнал. При неискаженном приеме сигнала(вероятность) ст. А повторяет ко­дограмму; при трансформации сигналав один из разрешен­ных сигналовалфавита ст. В (вероятность) ст. А передает очередную кодограмму;

– состояние III: на ст. В принята неискаженная кодограм­ма (вероятность) и по обратному каналу посылается сигнал;

– состояние IV: на ст. А кодограмма принята неиска­женной (вероятность), по прямому каналу посылается очеред­ная кодограмма, в результате чего на ст. В будет правильно зарегистрирована кодограм­ма;

– состояние V: на ст. В регистрация кодограммы происходит с ошибкой, ко­торая может вызываться транс­формацией сигналав обрат­ном канале в одну из разре­шенных кодограмм(вероят­ность), трансформацией кодограммыв ложный сигнал запроса(вероятность) или, наконец, трансформацией кодограммыв прямом ка­нале в одну из разрешенных кодограмм(вероятность).

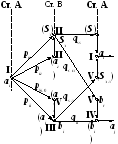
Рисунок 1.19 – Схема вероятностных переходов системы РОС

Дальнейшее продолжение схемы вероятностных переходов на последующие циклы работы си­стемы нецелесообразно, так как процесс передачи информации нач­нет ветвиться, схема переходов усложняется, а характерные ее состояния сохраняются.

Построим соответствующий этой схеме граф (рис. 1.20, а), штриховыми линиями показаны ветви графа с малыми переходными веро­ятностями.

С точки зрения верности передачи сообщений, нас ин­тересуют три узла графа – I, IV и V, связанные с работой ст. А, причем узел I соответствует передаче сигнала , узелIV – правильной регистрации сообщений , а узелV – ошибочной регистрации . Узлы графаII и III связаны с работой ст. В и влияют на окончательный результат посред­ством переходных вероятностей обратного канала. Поэтому указан­ный граф можно преобразовать в трехузловой граф (рис. 1.20, б), где узел I соответствует передаче сигналов, узлы 2 и 3 – пра­вильной и ошибочной регистрации сигналов, а переходные вероятности при этом

; ;. (1.36)

Ст. А

Ст. В

II

P_О.О

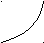
q_ss

q_sп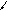

I

V

P_K.О

a_{i 0}

p₁₁

a_i

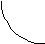
q_ss

a_{i n}

p_ii

III

IV

q_ii

p₁₃

p₁₂

1

2

3

(a_i)

a_i

(a_j)

а)

б)

Рисунок 9.11 – Граф системы ПД с РОС для определения

С помощью этого графа можно определить вероятность ошибоч­ной регистрации кодограммы при повторениях:

, (1.37)

где – вероятность правильного приема, равная вероятности перехода из узла I графа в узелII за циклов.

Согласно рис. 1.20, б, матрица переходных вероятностей систе­мы имеет вид

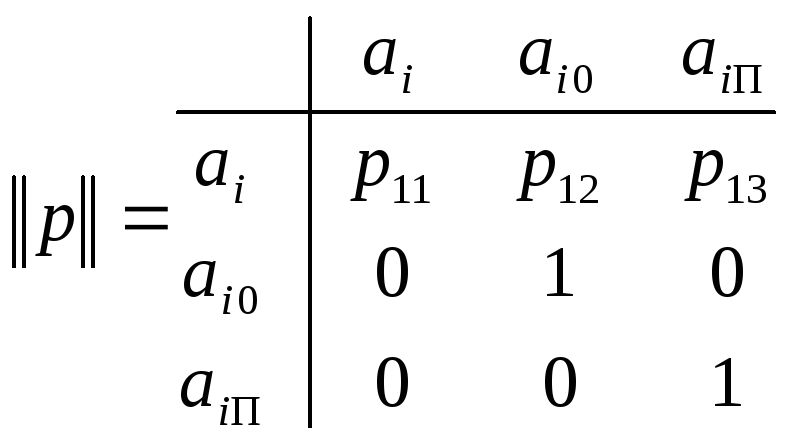. (1.38)

Так как узел I соответствует несущественному состоянию системы, а узлы II и III – существенным состояниям, то стохастическую разложимую матрицу (1.38) можно привести к нормальному виду:

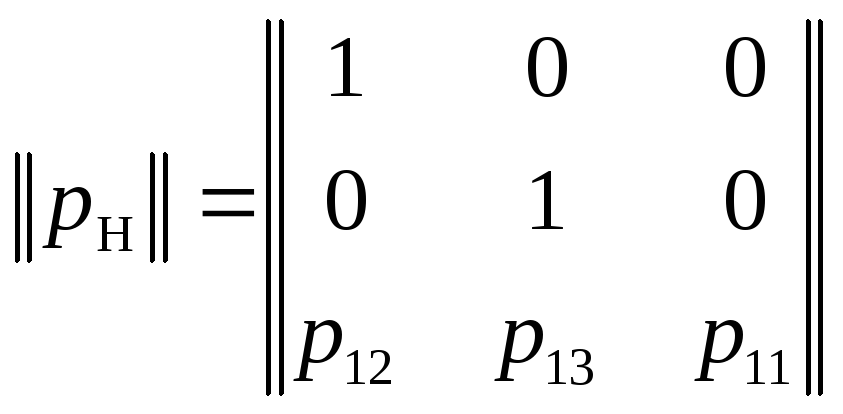. (1.39)

Для вычисления вероятности воспользуемся формулой Пер­рона и выражением для финальной вероятности ошибки при:

, (1.40)

где – алгебраическое дополнение характеристического пределителя матрицы.