1.7 Методика анализа адаптивных систем передачи данных

Алгоритм работы адаптивных систем ПД с ОС с учетом запаздывания сигналов и действия помех в прямом и обратном каналах наиболее полно ото­бражается схемой вероятностных переходов, представляющей собой стохастическую модель системы. Однако даже для простейшего алгоритма, при числе повторяемых кодограмм , эта схема стано­вится слишком разветвленной, и определение точных значенийизатруднительно. Если, однако, искажения сигналов, обусловленные их трансформацией, пропусками или оши­бочным повторением, эквивалентны, то определение значенийиможно осуществить в два этапа. Вначале про­цесс передачи сигналов в системе рассматривается как простая однородная цепь Маркова с дискретным временем, т. е. значенияиопределяются прии. Затем устанав­ливается зависимость обнаруживаемых и необнаруживаемых ошибок от запаздывания сигналов; решение этой задачи приисопряжено с анализом сложных цепей Маркова.

Пусть передается сообщение , содержащееэле­ментов, и. Если исказиласьi-я кодограмма, то на при­емной стороне могут быть зарегистрированы следующие случаи образования последовательностей символов:

;

;

.

В первом случае из-за трансформации кодограммы в разрешенную кодограммуобщее число элементов в сообщениине измени­лось; во втором –оно стало, а в третьем –. Если при этом исказится сам командный сигнал (, или), то произойдет дополнительно перераспределение последующих кодограмм в виде их временного сдвига. Появление пакетов ошибок длиной от 1 до элементов существенно затрудняет анализ ра­боты системы.

Если, однако, на первом этапе исследования адаптивной системы ПД с ОС счи­тать , то можно принять гипотезу о том, что правильная регистрация сообщения возможна только при безошибочной пере­даче всех его элементов. В действительности может иметь место компенсация ошибок, приводящая к правильной регистрации сооб­щений, однако привероятность этого события ничтожно мала.

Для определения вероятности в адаптивной системе ПД с ОС с запазды­ванием сигналов необходимо:

– составить схему вероятностных переходов, отображающую прохождение сигнала в прямом и обратном каналах;

– построить соответствующий этой схеме граф, учитываю­щий передачу, безошибочный прием сигналов и прием сигналов с необнаруживаемой ошибкой;

– преобразовать этот граф к виду, при котором переход че­рез каждый из его узлов отождествляется с работой ст. А в режиме передачи;

– составить стохастическую матрицу графа системы;

– используя математический аппарат дискретных цепей Мар­кова, определить величину как финальную вероятность (переходную вероятность зациклов);

– определить зависимость (отыскание этой зави­симости производится аналогично предыдущему с той лишь раз­ницей, что сначала ищется

вероятность перехода зацик­лов от передачи сигналак передаче сигнала, а за­тем среднее значение числа передач, что отражает выражение 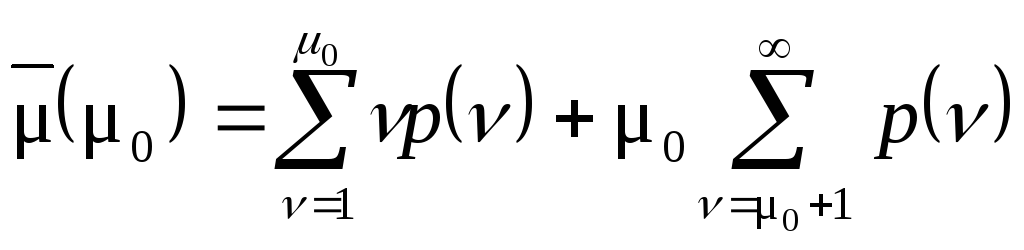(1.35)).

. (1.35)

При этом необходимо иметь в виду, что граф системы должен со­держать два узла, поскольку отыскание зависимости связа­но с определением переходной вероятности от сигналак сиг­налузациклов.