
- •Глава I. Елементи лінійної та векторної алгебри
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •§23. Приклади розв’язання задач на розкладення векторів по довільному базису і перетворення координат
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
§23. Приклади розв’язання задач на розкладення векторів по довільному базису і перетворення координат
Задача
23.1. При
якому
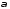 вектори
вектори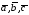 не утворюють базис,
якщо
не утворюють базис,
якщо
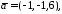
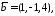
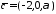 .
.
Розв’язання.
Згідно
означення базису, маємо знайти
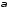 ,
при якому дані вектори компланарні,
тобто
,
при якому дані вектори компланарні,
тобто
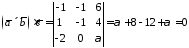 ,
,
тобто
дані в умові вектори не утворюють базис
при
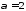 .
.
Задача
23.2. Дано
три вектори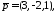
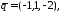
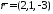 .
Знайти розкладання вектора
.
Знайти розкладання вектора
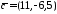 за базисом
за базисом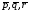 .
.
Розв’язання.
Розкладання
вектора за базисом здійснюється за
допомогою формули 2198, де коефіцієнти
розкладання
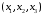 нам
потрібно буде знайти.
нам
потрібно буде знайти.
Запишемо цю формулу у координатному вигляді
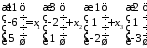 ,
,
що приведе до системи рівнянь
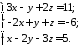 .
.
Розв’яжемо цю систему методом Гауса:
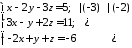
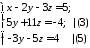
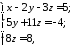
звідки знаходимо
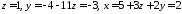 .
.
Отже,
розкладання вектора
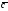 за
базисом
за
базисом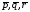 має
вигляд:
має
вигляд:
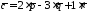 .
.
Задача
23.3. В
системі
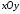 дано
точку
дано
точку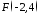 .
Знайти її координати в системі
.
Знайти її координати в системі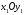 ,
яка отримана з
,
яка отримана з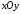 в результаті повороту на кут
в результаті повороту на кут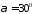 .
.
Розв’язання.
Скористаємось формулами повороту системи координат 22115. Отримуємо:
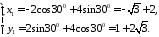
Задача
23.4. В
системі
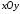 дано
точку
дано
точку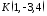 .
Знайти її координати в системі
.
Знайти її координати в системі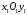 ,
центр якої в
,
центр якої в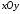 має координати
має координати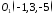 і напрямки відповідних координатних
осей співпадають.
і напрямки відповідних координатних
осей співпадають.
Розв’язання.
Оскільки напрямки координатних осей співпадають, то нова система координат отримана за допомогою паралельного перенесення. Застосувавши відповідні формули 22112, маємо:
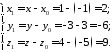
Отже, в
системі
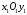 точка
точка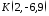 .
.
Задачі для самостійної роботи
Перевірити, чи утворюють вектори
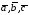 базис тривимірного простору та знайти
компоненти вектора
базис тривимірного простору та знайти
компоненти вектора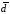 у
цьому базисі.
у
цьому базисі.
а)
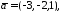
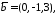
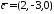 ,
,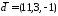
б)
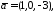
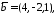
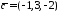 ,
,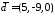
В системі
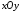 дано
точку
дано
точку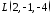 .
Знайти її координати в системі
.
Знайти її координати в системі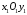 ,
центр якої в
,
центр якої в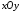 має координати
має координати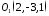 і напрямки відповідних координатних
осей співпадають.
і напрямки відповідних координатних
осей співпадають.В системі
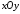 дано
точку
дано
точку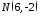 .
Знайти її координати в системі
.
Знайти її координати в системі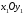 ,
яка отримана з
,
яка отримана з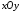 в результаті повороту на кут
в результаті повороту на кут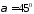 .
.
Питання для повторення
Базис. Розкладення вектора по некомпланарним векторам.
Формули паралельного перенесення і повороту.
11724Equation Section (Next)§24.
Метричний
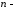 вимірний
простір. Лінійний
вимірний
простір. Лінійний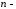 вимірний
векторний простір і його базис. Евклідів
простір
вимірний
векторний простір і його базис. Евклідів
простір
Розглянемо
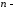 вимірний
простір
вимірний
простір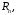 що складається з точок
що складається з точок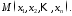
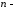 вимірний
простір
вимірний
простір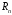 називаєтьсяметричним
простором,
якщо кожним двом елементам
називаєтьсяметричним
простором,
якщо кожним двом елементам
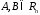 ставиться у відповідність число
ставиться у відповідність число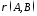 ,
яке називаєтьсяметрикою
або відстанню і задовольняє умовам:
,
яке називаєтьсяметрикою
або відстанню і задовольняє умовам:
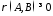 і
і
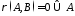 і
і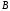 - співпадають;
- співпадають;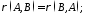
для будь яких трьох елементів
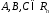
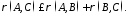
Візьмемо
дві довільні точки
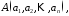
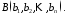 Знайдемо відстань між двома точками за
наступною формулою:
Знайдемо відстань між двома точками за
наступною формулою:
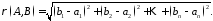 11824118\* MERGEFORMAT (.)
11824118\* MERGEFORMAT (.)
Можна
довести, що для відстані, заданої формулою
24118, виконуються усі умови
 Але 24118 не єдиний спосіб завдання
відстані у
Але 24118 не єдиний спосіб завдання
відстані у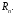 Так, якщо взяти
Так, якщо взяти
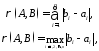
то умови
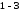 теж виконуються, і кожне з цих чисел
можна розглядати як відстань між двома
точками у
теж виконуються, і кожне з цих чисел
можна розглядати як відстань між двома
точками у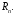 Але перевагою 24118 є те, що при
Але перевагою 24118 є те, що при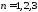 отримуються формули для відстані між
точками на координатній прямій,
координатній площині, у координатному
просторі.
отримуються формули для відстані між
точками на координатній прямій,
координатній площині, у координатному
просторі.
Нехай
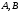 - довільні точки з
- довільні точки з
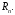 Назвемо
Назвемо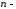 вимірним
вектором
вимірним
вектором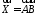 впорядковану сукупність
впорядковану сукупність чисел
чисел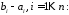
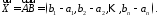 11924119\* MERGEFORMAT (.)
11924119\* MERGEFORMAT (.)
Числа
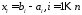 називаються координатами
називаються координатами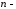 вимірного
вектора і те, що вектор має координати
вимірного
вектора і те, що вектор має координати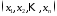 ,
позначають наступним чином
,
позначають наступним чином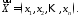
Модулем
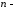 вимірного
вектора називається корінь квадратний
з суми квадратів його координат:
вимірного
вектора називається корінь квадратний
з суми квадратів його координат:
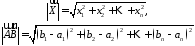 12024120\* MERGEFORMAT (.)
12024120\* MERGEFORMAT (.)
Можна
бачити, що якщо використовувати метрику
24118, то модуль
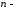 вимірного
вектора дорівнює відстані між його
початком і кінцем.
вимірного
вектора дорівнює відстані між його
початком і кінцем.
Рівними
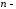 вимірними
векторами
вимірними
векторами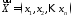 і
і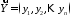 назвемо такі, що мають однакові відповідні
координати:
назвемо такі, що мають однакові відповідні
координати:
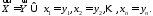
Введемо
для
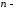 вимірних
векторів лінійні операції (множення на
число, додавання) так само, як вони
здійснюються над векторами у просторі
у координатній формі.
вимірних
векторів лінійні операції (множення на
число, додавання) так само, як вони
здійснюються над векторами у просторі
у координатній формі.
Для будь якого
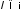
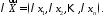
Для будь яких
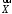 і
і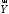
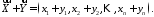
Цим операціям притаманні такі властивості.
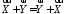 (комутативність
додавання);
(комутативність
додавання);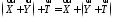 (асоціативність
додавання);
(асоціативність
додавання);Якщо
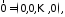 то
то
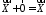 (існування
нульового елемента);
(існування
нульового елемента);
Для будь якого вектора
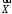
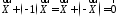 (існування
протилежного елемента);
(існування
протилежного елемента);
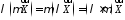 (асоціативність
множення на число);
(асоціативність
множення на число);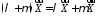 (дистрибутивність
відносно додавання чисел);
(дистрибутивність
відносно додавання чисел);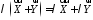 (дистрибутивність
відносно додавання векторів).
(дистрибутивність
відносно додавання векторів).
Множина
у який введено лінійні операції, що
задовольняють властивості
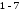 називаєтьсялінійним
простором.
Отже,
називаєтьсялінійним
простором.
Отже,
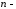 вимірний
векторний простір з введеними вище
операціями є лінійним простором.
вимірний
векторний простір з введеними вище
операціями є лінійним простором.
Нехай
є система

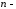 вимірних
векторів.
вимірних
векторів.
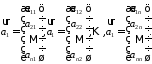
Має
місце теорема, аналогічна теоремі про
розкладення будь-якого вектора по
 некомпланарним.
некомпланарним.
Теорема.
Якщо вектори
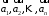 такі, що
такі, що
 , 12124121\* MERGEFORMAT (.)
, 12124121\* MERGEFORMAT (.)
то
будь-який вектор
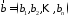 може бути однозначно поданий у вигляді
може бути однозначно поданий у вигляді
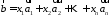 . 12224122\* MERGEFORMAT (.)
. 12224122\* MERGEFORMAT (.)
Будь-які
 векторів,
що задовольняють умові 24121 називаютьсябазисом
векторів,
що задовольняють умові 24121 називаютьсябазисом
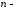 вимірного
векторного простору. Рівність 24122
називається розкладенням вектора
вимірного
векторного простору. Рівність 24122
називається розкладенням вектора
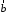 у базисі
у базисі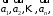 а числа
а числа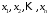 координатами вектора
координатами вектора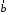 у цьому базисі.
у цьому базисі.
Складемо
лінійну комбінацію векторів
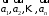 і прирівняємо її до нульового вектора
і прирівняємо її до нульового вектора
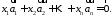 12324123\* MERGEFORMAT (.)
12324123\* MERGEFORMAT (.)
Зрозуміло,
що коли усі
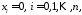 то ця рівність здійснюється. Але якщо
виконується умова 24121, рівність можлива
тільки у цьому випадку.
то ця рівність здійснюється. Але якщо
виконується умова 24121, рівність можлива
тільки у цьому випадку.
Якщо
лінійна комбінація векторів
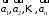 дорівнює 0-вектору тоді і тільки тоді,
коли
дорівнює 0-вектору тоді і тільки тоді,
коли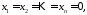 то ці вектори називаютьсялінійно
незалежними.
Отже, будь-які
то ці вектори називаютьсялінійно
незалежними.
Отже, будь-які
 лінійно незалежні вектори утворюють
базис
лінійно незалежні вектори утворюють
базис вимірного
простору. Умова 24121 є необхідною і
достатньою умовою лінійної незалежності
векторів.
вимірного
простору. Умова 24121 є необхідною і
достатньою умовою лінійної незалежності
векторів.
Лінійний
векторний простір називається Евклідовим,
якщо кожній парі векторів
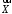 і
і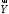 ставиться у відповідність число
ставиться у відповідність число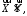 яке називається скалярним добутком і
задовольняє умовам:
яке називається скалярним добутком і
задовольняє умовам:
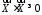 причому
причому
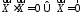 ;
;
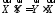 ;
;
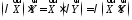 ;
;
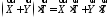 .
.
Введемо
у
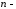 вимірному
векторному просторі скалярний добуток
двох векторів
вимірному
векторному просторі скалярний добуток
двох векторів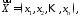
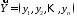 згідно з формулою
згідно з формулою
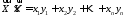 12424124\* MERGEFORMAT (.)
12424124\* MERGEFORMAT (.)
За
такого введення скалярного добутку для
нього виконуються усі умови
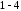 і векторний простір буде Евклідовим.
і векторний простір буде Евклідовим.
З 24124 також випливає, що
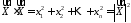 12524125\* MERGEFORMAT (.)
12524125\* MERGEFORMAT (.)
Для
будь-яких
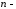 вимірних
векторів
вимірних
векторів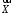 і
і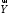 виконується нерівність (Коши-Буняковського):
виконується нерівність (Коши-Буняковського):
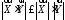 12624126\* MERGEFORMAT (.)
12624126\* MERGEFORMAT (.)
З
нерівності 24126 при
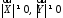 випливає, що
випливає, що
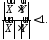
Тоді
існує кут
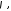 такий що
такий що
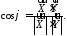 12724127\* MERGEFORMAT (.)
12724127\* MERGEFORMAT (.)
Найменший
з кутів
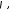 що задовольняють рівності 24127, називається
кутом між двома
що задовольняють рівності 24127, називається
кутом між двома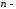 вимірними
векторами. Ненульові вектори
вимірними
векторами. Ненульові вектори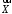 і
і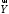 будуть перпендикулярними тоді і тільки
тоді, коли
будуть перпендикулярними тоді і тільки
тоді, коли
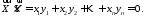 12824128\* MERGEFORMAT (.)
12824128\* MERGEFORMAT (.)
Вектори
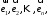 такі, що
такі, що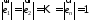 і
і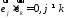 є
лінійно незалежними і утворюють базис,
який називаєтьсяортонормованим.
Прикладом такого базису є вектори
є
лінійно незалежними і утворюють базис,
який називаєтьсяортонормованим.
Прикладом такого базису є вектори
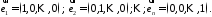
12925Equation Section (Next)13026Equation Section (Next)§25. Приклади розв’язування задач на вектори в n-вимірному просторі
Задача
25.1. У
п’ятивимірному просторі дано точки
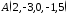 та
та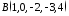 .
Знайти
.
Знайти та компоненти вектора
та компоненти вектора .
.
Розв’язання.
За
24119 знайдемо
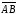 :
: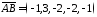 ,
тоді за 24120
,
тоді за 24120
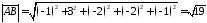 .
.
Компоненти вектора
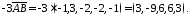
Задача
25.2.
Знайти
кут між векторами
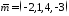 та
та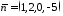
Розв’язання.
Користуючись
формулою 24127 для знаходження кута між
двома
 вимірними
векторами (в нашому випадку
вимірними
векторами (в нашому випадку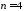 ),
маємо:
),
маємо:
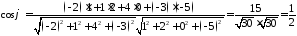 ,
,
отже,
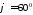 .
.
Задача
25.3.
Перевірити, чи утворюють вектори
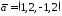 ,
,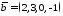 ,
,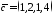 ,
,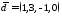 базис
чотирьохвимірного простору.
базис
чотирьохвимірного простору.
Розв’язання.
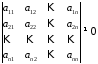
Перевіримо, чи є дані вектори лінійно незалежними. Згідно необхідної і достатньої умови лінійної незалежності векторів 24121, необхідно обчислити значення визначника:
 .
.
Отже, дані в умові вектори є лінійно незалежними і утворюють базис чотирьохвимірного простору.
