
- •Глава I. Елементи лінійної та векторної алгебри
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •§23. Приклади розв’язання задач на розкладення векторів по довільному базису і перетворення координат
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
ЗМІСТ
Вступ…………………………………………………………………………….…..5
Глава I. ЕЛЕМЕНТИ ЛІНІЙНОЇ ТА ВЕКТОРНОЇ АЛГЕБРИ……………………………7
§1. Системи лінійних алгебраїчних рівнянь. Матриця системи………………….7
§2. Види матриць. Лінійні дії над матрицями та їх властивості.
Транспонування матриць. Добуток матриць………...…………..…………….8
§3. Визначник матриці. Мінори і алгебраїчні доповнення.
Теореми про алгебраїчні доповнення……………………………………...….12
§4. Загальні властивості визначників……………………………………………..15
§5. Мінори матриці. Ранг матриці, його обчислення і властивості……………..17
§6. Обчислення визначників. Дії над матрицями………………………………...18
§7. Матричний запис системи лінійних алгебраїчних рівнянь.
Теорема Кронекера-Капеллі. Дослідження неоднорідних і однорідних
систем лінійних рівнянь…………….………………………………………….24
§8. Поняття оберненої матриці. Матричний метод розв’язання лінійних
алгебраїчних систем. Формули Крамера……….……………………………..27
§9. Задачі на дослідження на сумісність і розв’язування систем лінійних
рівнянь. Метод Гауса……………………………………………………….….30
§10. Системи координат на прямій, площині і у просторі. Координати точки...42
§11. Скалярні та векторні величини. Поняття вектора. Лінійні операції
з векторами у геометричній формі і їх властивості………………………...48
§12. Проекція вектора на вісь і її властивості………….…………………………50
§13. Координати вектора. Визначення вектора за його координатами.
Лінійні операції над векторами у координатній формі……...……………..53
§14. Розкладання вектора по базисним векторам (ортам) системи
координат. Визначення вектора координатами початку і кінця.
Обчислення відстані між двома точками у просторі….……………………56
§15. Поділ відрізка у даному відношенні. Відшукання координат центра
тяжіння системи матеріальних точок………………..………………………58
§16. Задачі на обчислення координат точок в різних системах.
Дії над векторами в координатній формі………………………..…………..61
§17. Скалярний добуток векторів і його основні властивості……….…………..66
§18. Векторний добуток векторів і його основні властивості……….…………..70
§19. Мішаний (векторно-скалярний) добуток трьох векторів…………………..74
§ 20. Задачі на застосування скалярного, векторного та мішаного добутків…..77
§ 21. Розкладення вектора по некомпланарним векторам.
Базис тривимірного простору. Базис на координатній площині…………..88
§22. Матриця переходу від одного базису до іншого. Перетворення
координат. Формули паралельного перенесення і повороту………………89
§23. Приклади розв’язання задач на розкладення векторів по
довільному базису і перетворення координат……………………...……….94
§24.
Метричний
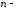 вимірний
простір. Лінійний
вимірний
простір. Лінійний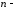 вимірний
векторний
вимірний
векторний
простір і його базис. Евклідів простір……………………………………....97
§25. Приклади розв’язування задач на вектори в n-вимірному просторі……..101
Глава II. ЕЛЕМЕНТИ АНЛІТИЧНОЇ ГЕОМЕТРІЇ………………………………………103
§26. Поняття рівняння поверхні і лінії у просторі. Рівняння
сферичної поверхні..……………………………………………………..….103
§27. Загальне рівняння площини і його дослідження…..………………………106
§28. Рівняння площини у відрізках на координатних осях. Рівняння
площини, що проходить через три задані точки. Обчислення відстані
від точки до площини..………………………………………………………108
§29. Кут між двома площинами. Умови паралельності і
перпендикулярності площин..………………………………………………110
§30. Розв'язання задач на складання рівнянь площини та взаємне
розміщення площин у просторі……………………………………………..111
§31. Рівняння прямої у просторі…………………………………………………118
§32. Відстань від точки до прямої у просторі. Взаємне розміщення прямих.
Обчислення кута між двома прямими..…………………………………….120
§ 33. Задачі на пряму у просторі. Складання рівнянь, дослідження
взаємного розміщення прямих у просторі…………………………………123
§34. Взаємне розміщення прямої і площини……………………………………128
§35. Задачі на взаємне розміщення прямої та площини………………………..129
§36. Загальне і параметричне рівняння лінії на координатній площині.
Рівняння кола. Загальне рівняння прямої на площині…………………….134
§37. Різні види рівняння прямої на координатній площині……………………137
§38. Обчислення відстані від точки до прямої і кута між двома прямими
на координатній площині…….……………………………………………..140
§ 39. Пряма на координатній площині. Приклади розв’язування задач………142
§40. Визначення еліпса і виведення його канонічного рівняння.
Дослідження форми еліпса за його рівнянням…………………………….150
§ 41. Визначення гіперболи і виведення її канонічного рівняння.
Дослідження форми гіперболи за її рівнянням……………………………154
§ 42. Визначення параболи і виведення її канонічного рівняння.
Дослідження форми і властивостей параболи……………………………..157
§ 43. Складання і дослідження канонічних рівнянь кривих другого порядку 159
§ 44. Загальне рівняння кривої другого порядку……………………………….164
§ 45. Циліндричні поверхні. Рівняння еліптичного або кругового циліндру…174
§ 46. Конічні поверхні. Рівняння кругового конуса…………………………….175
§ 47. Поверхні обертання. Поверхні обертання другого порядку……………..176
§ 48. Розв’язування задач на складання рівнянь поверхонь
та їх дослідження…………………………………………………………….180
Відповіді…………………………………………………………………………...183
Додаток …………………………………………………………………………...186
Література………………………………………………………………………...200
Вступ
Запропонований навчальний посібник призначений для вивчення таких розділів вищої математики, як лінійна, векторна алгебра та аналітична геометрія. Метою його є забезпечення знаннями з цих розділів, необхідних для вивчення інших фундаментальних (фізика, теоретична механіка, опір матеріалів, інженерна графіка) і спеціальних дисциплін, для студентів вищих навчальних закладів, які навчаються за напрямком 6.070104 «Морський та річковий транспорт» очної та заочної форм навчання. Також посібник має дати можливість студентам і курсантам набути навичок застосовувати апарат лілійної та векторної алгебри і аналітичної геометрії для розв’язання задач, які виникають у їх практичній діяльності.
Автори прагнули викласти матеріал по можливості доступно, але не за рахунок математичної строгості. Теоретичні положення ілюструються численними прикладами і розібраними типовими задачами, які закріплюють і пояснюють теоретичний матеріал. При підборі задач увага приділялась не лише формально-математичній стороні, а й прикладному змісту. Після кожної логічно завершеної частини теоретичного матеріалу надаються питання для самоконтролю, а також задачі і вправи для самостійного розв’язання з наданими відповідями. Все це сприяє засвоєнню теоретичного матеріалу і робить посібник зручним для самостійного вивчення розглянутих розділів курсу вищої математики.
Посібник складається з двох частин, розділених на 48 параграфів, списку рекомендованої літератури та додатків.
В §1-9 викладається матеріал з лінійної алгебри. Вводиться поняття системи лінійних алгебраїчних рівнянь і її матриці, а також визначника матриці. Розглядаються питання сумісності систем лінійних алгебраїчних рівнянь, а також основні методи їх розв’язання.
§10-25
містить основні положення векторної
алгебри. Вводяться поняття координат
точки і вектора, вивчаються дії над
векторами в геометричній та координатній
формах. Дається поняття базису системи
координат і вивчаються такі важливі
для навігації поняття, як перехід від
одного базису до іншого і перетворення
координат. Поняття простору і векторів
у ньому узагальнюється на випадок
 вимірного.
вимірного.
Змістом §26-48 є матеріал з аналітичної геометрії. Вводяться поняття рівнянь поверхні і лінії у просторі, а також лінії на координатній площині. Розглядаються різні випадки рівнянь площини і прямої у просторі і досліджується їх взаємне положення.
Значна увага приділяється таким значним для навігації питанням, як обчислення відстані від точки до площини і від точки до прямої, а також відстані між двома паралельними площинами і прямими. Пряма на координатній площині вивчається як частинний випадок прямої у просторі. Дано визначення основних кривих другого порядку і виведені їх канонічні рівняння. Розглянуто приведення рівняння кривої другого порядку до канонічного вигляду. Вивчаються циліндричні, конічні поверхні, поверхні обертання і поверхні другого порядку.
Додатки містять теоретичні питання і зразки практичних завдань з модульного контролю за матеріалом змістовних модулів «Лінійна і векторна алгебра», «Аналітична геометрія».
Список літератури містить додаткову навчальну літературу і літературу для більш глибокого вивчення розглянутих розділів курсу вищої математики.
Сподіваємось, що даний посібник допоможе ґрунтовно засвоїти викладені розділи і буде корисним також при подальшому навчанні.
Глава I. Елементи лінійної та векторної алгебри
11Equation Section 1§1. Системи лінійних алгебраїчних рівнянь. Матриця системи
Системою
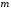 лінійних алгебраїчних рівнянь з
лінійних алгебраїчних рівнянь з невідомими називається будь-яка система
рівнянь наступного вигляду:
невідомими називається будь-яка система
рівнянь наступного вигляду:
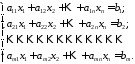 212\* MERGEFORMAT (.)
212\* MERGEFORMAT (.)
Тут:
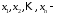 невідомі;
числа
невідомі;
числа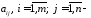 коефіцієнти
системи;
коефіцієнти
системи;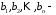 праві
частини.
праві
частини.
Розв’язком
системи
12 називаються будь-які
 чисел
чисел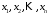 ,
підстановка яких у систему перетворює
кожне її рівняння у вірну числову
рівність.
,
підстановка яких у систему перетворює
кожне її рівняння у вірну числову
рівність.
Якщо система лінійних рівнянь 12 не має жодного розв’язку, то вона називається несумісною.
Головними задачами теорії лінійних алгебраїчних систем є наступні:
Довести сумісність або несумісність системи.
Якщо система сумісна, знайти усі її розв’язки.
В залежності від вигляду правих частин системи 12 їх поділяють на неоднорідні та однорідні.
Система
12 називається неоднорідною
системою лінійних алгебраїчних рівнянь,
якщо серед чисел
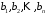 є хоча б одне
є хоча б одне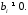
Система
12 називається однорідною
системою лінійних алгебраїчних рівнянь,
якщо усі числа
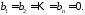
Зауважимо, що кожній неоднорідній системі можна поставити у відповідність однорідну:
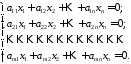 313\* MERGEFORMAT (.)
313\* MERGEFORMAT (.)
13 – однорідна система, що відповідає неоднорідній системі 12.
Побудова
теорії лінійних систем алгебраїчних
рівнянь неможлива
без поняття матриці. Дійсно, коефіцієнти
систем 12, 13
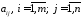 можна розмістити у наступній таблиці,
що складається з
можна розмістити у наступній таблиці,
що складається з рядків і
рядків і стовпців, яку позначимо буквою
стовпців, яку позначимо буквою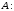
 414\* MERGEFORMAT (.)
414\* MERGEFORMAT (.)
Таку
таблицю далі будемо називати матрицею
розміру
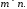
Таким
чином, матрицею
розміром
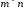 називається таблиця з
називається таблиця з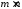 чисел
чисел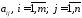 записаних у
записаних у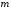 рядків і
рядків і стовпчиків.
стовпчиків.
Числа
 які складають матрицю, називають її
елементами.
які складають матрицю, називають її
елементами.
Матриці,
як правило, позначають великими
латинськими літерами
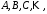 а елементи, з яких вони складаються,
малими:
а елементи, з яких вони складаються,
малими: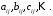 При
вивченні загальних властивостей матриць,
коли не важливі конкретні значення її
елементів, можливо використання
наступного скороченого позначення:
При
вивченні загальних властивостей матриць,
коли не важливі конкретні значення її
елементів, можливо використання
наступного скороченого позначення:
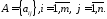
52Equation Section (Next)§2. Види матриць. Лінійні дії над матрицями та їх властивості. Транспонування матриць. Добуток матриць
Розглянемо
довільну матрицю розміру
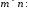
 626\* MERGEFORMAT (.)
626\* MERGEFORMAT (.)
Матрицю,
у якої кількість рядків і стовпчиків
різна
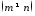 ,
називаютьпрямокутною.
,
називаютьпрямокутною.
Якщо матриця складається з одного рядка (стовпчика) вона називається матрицею-рядком (стовпцем):
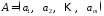 -
матриця-рядок,
-
матриця-рядок,
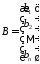 - матриця-стовпець.
- матриця-стовпець.
Коли у
матриці кількість рядків і стовпців
збігається і дорівнює
 ,
то вона називаєтьсяквадратною
матрицею
,
то вона називаєтьсяквадратною
матрицею
 порядку:
порядку:
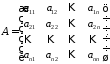 727\* MERGEFORMAT (.)
727\* MERGEFORMAT (.)
27 – квадратна матриця.
Елементи
 квадратної матриці називаютьсядіагональними
і кажуть, що вони утворюють головну
діагональ
матриці.
Інколи розглядають і допоміжну діагональ
квадратної матриці на якій містяться
елементи
квадратної матриці називаютьсядіагональними
і кажуть, що вони утворюють головну
діагональ
матриці.
Інколи розглядають і допоміжну діагональ
квадратної матриці на якій містяться
елементи
 .
.
Квадратна
матриця називається симетричною у
випадку коли
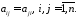 Зміст останньої умови полягає у тому,
що елементи, розміщені симетрично
відносно головної діагоналі, співпадають.
Зміст останньої умови полягає у тому,
що елементи, розміщені симетрично
відносно головної діагоналі, співпадають.
Квадратна
матриця у якій всі елементи, окрім тих
що знаходяться на головній діагоналі,
дорівнюють
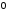 називаєтьсядіагональною:
називаєтьсядіагональною:
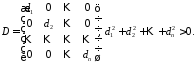
Квадратна
матриця у якої елементи на головній
діагоналі дорівнюють
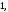 а всі інші елементи є нулі, називаєтьсяодиничною
матрицею
а всі інші елементи є нулі, називаєтьсяодиничною
матрицею
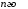 порядку:
порядку:

Матриця
кожний елемент якої дорівнює
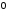 називається нуль-матрицею, абонульовою
матрицею.
називається нуль-матрицею, абонульовою
матрицею.
Для матриць одного розміру можна ввести поняття рівності і додавання.
Дві
матриці одного розміру
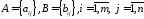 називаютьсярівними
називаютьсярівними
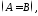 якщо в них співпадають однаково розміщенні
елементи:
якщо в них співпадають однаково розміщенні
елементи:
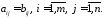
Сумою
двох вище вказаних матриць називається
третя матриця
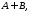 яка складається з елементів
яка складається з елементів

Добутком
матриці на число
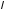 називається матриця, яка позначається
називається матриця, яка позначається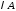 і складається з елементів
і складається з елементів
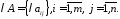
Операції додавання і множення на число називаються лінійними операціями над матрицями.
Лінійні операції над матрицями мають наступні властивості:
 (комутативність);
(комутативність);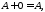
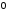 -
нуль-матриця однакового з
-
нуль-матриця однакового з
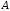 розміру;
розміру; (асоціативність);
(асоціативність);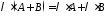 (асоціативність
множення на число відносно суми матриць);
(асоціативність
множення на число відносно суми матриць);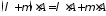 (асоціативність
відносно суми чисел);
(асоціативність
відносно суми чисел);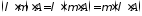 (асоціативність
відносно множення чисел).
(асоціативність
відносно множення чисел).
Ще однією важливою операцією над матрицями є операція транспонування.
Транспонованою
матрицею
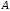 називається матриця
називається матриця

Операція
транспонування, очевидно, полягає у
тому, що стовпці матриці
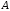 послідовно, починаючи з першого, записують
у рядки.
послідовно, починаючи з першого, записують
у рядки.
Над матрицями можна ввести операцію множення. Але перемножувати можна тільки узгоджені матриці.
Дві
матриці
 і
і називаютьсяузгодженими,
якщо число стовпців першої матриці
дорівнює числу рядків другої.
називаютьсяузгодженими,
якщо число стовпців першої матриці
дорівнює числу рядків другої.
Розглянемо матриці:
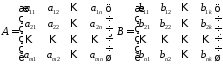
Матриця
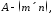 матриця
матриця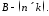
Ці дві
матриці є узгодженими. Зауважимо, що
матриці
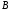 і
і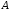 у загальному вигляді не є узгодженими.
Число стовпців у матриці
у загальному вигляді не є узгодженими.
Число стовпців у матриці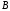 дорівнює
дорівнює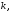 а число рядків у матриці
а число рядків у матриці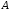 дорівнює
дорівнює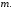 Зрозуміло, що дві квадратні матриці
одного порядку завжди узгоджені.
Зрозуміло, що дві квадратні матриці
одного порядку завжди узгоджені.
Добуток двох узгоджених матриць визначається за наступним правилом.
Добутком
матриці
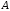 розміру
розміру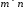 на матрицю
на матрицю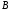 розміру
розміру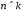 називається третя матриця
називається третя матриця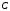 розміру
розміру ,
кожний елемент якої
,
кожний елемент якої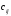 дорівнює сумі добутків елементів
дорівнює сумі добутків елементів рядка матриці
рядка матриці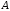 на відповідні елементи
на відповідні елементи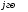 стовпчика матриці
стовпчика матриці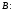
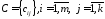
 828\* MERGEFORMAT (.)
828\* MERGEFORMAT (.)
Умовно формулу 28 можна записати ще в наступному вигляді:
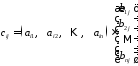 929\* MERGEFORMAT (.)
929\* MERGEFORMAT (.)
Розглянемо приклад множення матриць
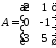 ,
,
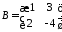
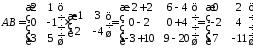
Операція добутку матриць має наступні властивості:
Якщо
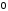 - нуль-матриця узгоджена з
- нуль-матриця узгоджена з то
то
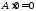
Для
квадратних матриць:
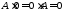
Якщо
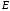 - одинична матриця узгоджена з
- одинична матриця узгоджена з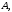 то
то

Для
квадратних матриць:
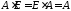
Операція множення матриць не є комутативною. Якщо існують обидва добутки
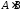 і
і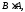 то рівність
то рівність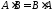 не завжди є вірною.
не завжди є вірною.Асоціативність відносно множення на число:
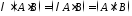
Асоціативність:

Дистрибутивність:
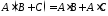

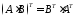 (для
квадратних матриць однієї розмірності)
(для
квадратних матриць однієї розмірності)
103Equation Section (Next)§3. Визначник матриці. Мінори і алгебраїчні доповнення. Теореми про алгебраїчні доповнення
Розглянемо довільну квадратну матрицю
 11311\* MERGEFORMAT (.)
11311\* MERGEFORMAT (.)
Кожній квадратній матриці 311 може бути поставлено у відповідність число, яке називається визначником (детермінантом) матриці і позначається

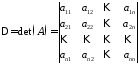 12312\* MERGEFORMAT (.)
12312\* MERGEFORMAT (.)
Порядком
визначника називається порядок
відповідної квадратної матриці. Визначник
312 є визначником
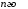 порядку.
порядку.
Строге визначення визначника довільного порядку можна дати за допомогою поняття переставлення [2]. Але можливе визначення визначників вищих порядків через визначники нижчих порядків.
Нехай є матриця першого порядку:
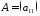 ,
тоді
,
тоді
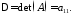
Якщо
 -
матриця другого порядку,
-
матриця другого порядку,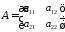 ,
то
,
то
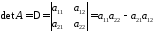 .
.
Формулу для обчислення визначника другого порядку зручно запам’ятовувати за допомогою наступної діаграми:

Визначник
для матриці третього порядку (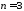 )
можна обчислювати за правилом трикутника:
)
можна обчислювати за правилом трикутника:
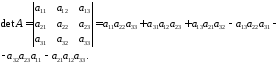 13313\* MERGEFORMAT (.)
13313\* MERGEFORMAT (.)
Легко бачити, що доданки у 313 утворюються за допомогою наступної схеми:

Щоб
вказати правило обчислення визначників
вищих порядків необхідно ввести поняття
мінору елемента визначника
 -го
порядку.
-го
порядку.
Мінором
елемента
 визначника
визначника -го
порядку називається визначник
-го
порядку називається визначник
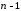 порядку, який утворюється з даного
визначника шляхом відкидання
порядку, який утворюється з даного
визначника шляхом відкидання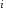 -го
рядка і
-го
рядка і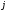 -го
стовпця.
-го
стовпця.
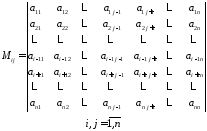 14314\* MERGEFORMAT (.)
14314\* MERGEFORMAT (.)
Алгебраїчним
доповненням
елемента
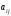 визначника
визначника -го
порядку називається число, яке дорівнює
-го
порядку називається число, яке дорівнює
 15315\* MERGEFORMAT (.)
15315\* MERGEFORMAT (.)
Теорема 1 (Про розкладення визначника по елементам рядка або стовпця).
Визначник дорівнює сумі добутків елементів рядка (стовпця) на їх алгебраїчні доповнення.
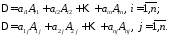 16316\* MERGEFORMAT (.)
16316\* MERGEFORMAT (.)
Перша
формула 316 є розкладенням за елементами
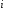 -го
рядка, а друга формула розкладенням за
елементами
-го
рядка, а друга формула розкладенням за
елементами -го
стовпця.
-го
стовпця.
Доведемо ці формули для визначників третього порядку, наприклад, для розкладення за елементами першого рядка (у загальному випадку доведення див. в [1]). Перегрупуємо наступним чином доданки у формулі 313:
 .
.
Кожний вираз в дужках дорівнює деякому визначнику другого порядку:
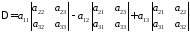 .
.
Тепер, якщо скористуватись 315, 316, знайдемо
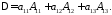
Аналогічними перетвореннями можна довести формулу розкладення за іншими рядками і за стовпцями. Формули 316 дозволяють послідовно знайти значення визначників будь-якого порядку.
Також корисною є така властивість алгебраїчних доповнень.
Теорема 2. Сума добутків елементів рядка (стовпця) на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) дорівнюють 0.
 17317\* MERGEFORMAT (.)
17317\* MERGEFORMAT (.)
184Equation Section (Next)§4. Загальні властивості визначників
Обчислення визначників високого порядку безпосередньо за формулами 316 вимагає великого об’єму обчислень. Цей об’єм інколи можна скоротити, якщо користуватися наступними властивостями, які наводяться без доведень (доведення див. [2], ст.34-35).
При транспонуванні квадратної матриці її визначник не змінюється:
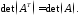
Внаслідок перестановки місцями двох рядків (стовпців) визначника його знак зміниться на протилежний:
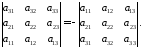
Визначник, який має нульовий рядок (стовпчик), дорівнює 0:
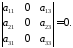
Визначник, який має два рядки (стовпця), відповідні елементи яких пропорційні, дорівнює 0:

Звідси
випливає, що визначник, у якого є два
однакових рядки
(стовпці) дорівнює

Спільний множник елементів якогось рядка (стовпця) можна винести за знак визначника:

Якщо елементи рядка (стовпця) визначника є сумою двох доданків, то такий визначник може бути поданий як сума двох визначників:

Визначник не зміниться, якщо до елементів якого-небудь його рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число:
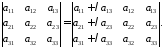
195Equation Section (Next)§5. Мінори матриці. Ранг матриці, його обчислення і властивості
Знову розглянемо довільну прямокутну матрицю

Нехай
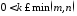 .
.
Мінором
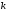 -го
порядку прямокутної матриці
-го
порядку прямокутної матриці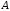 називається визначник, побудований з
елементів цієї матриці, які розміщені
на перетині будь-яких її
називається визначник, побудований з
елементів цієї матриці, які розміщені
на перетині будь-яких її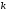 рядків і
рядків і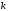 стовпців.
стовпців.
Якщо
матриця має відмінний від 0 мінор порядку
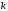 ,
а всі мінори вищого порядку дорівнюють
0, то число
,
а всі мінори вищого порядку дорівнюють
0, то число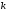 називаєтьсярангом
матриці. Це позначають наступним чином
називаєтьсярангом
матриці. Це позначають наступним чином
 .
.
Зрозуміло,
що
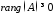 причому нулю може дорівнювати тільки
ранг 0-матриці:
причому нулю може дорівнювати тільки
ранг 0-матриці: .
.
Відмінний від нуля мінор найвищого порядку називається базисним. Таким чином, можна сказати, що ранг матриці співпадає з порядком базисного мінора.
Теорема (Про обвідні мінори).
Якщо
матриця
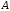 містить мінор порядку
містить мінор порядку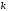 ,
який відмінний від 0, а усі інші мінори
порядку
,
який відмінний від 0, а усі інші мінори
порядку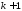 ,
що його обводять дорівнюють 0, то число
,
що його обводять дорівнюють 0, то число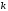 є ранг матриці.
є ранг матриці.
Покажемо застосування цієї теореми.

Відмінним
від 0 мінором
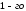 порядку є будь-який ненульовий елемент.
Наприклад,
порядку є будь-який ненульовий елемент.
Наприклад,
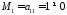 .
.
Мінор другого порядку, що його обводить:
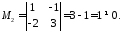
Цей
мінор обводять
 мінори третього порядку:
мінори третього порядку:
 .
.
Але можна бачити, що
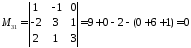 ,
,
 .
.
Таким
чином,
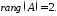
Ще один метод обчислення рангу базується на елементарних перетвореннях матриці, які його не змінюють. Такими перетвореннями є:
транспонування матриці;
переставлення місцями двох рядків (стовпців);
множення (ділення) усіх елементів рядка (стовпця) на число, відмінне від нуля;
додавання до елементів рядка (стовпця) відповідних елементів іншого рядка (стовпця), помножених на деяке число;
відкидання рядків (стовпців) матриці, усі елементи яких є нулі.
За допомогою цих перетворень матриця може бути приведена до вигляду коли визначення рангу стає очевидним.
206Equation Section (Next)§6. Обчислення визначників. Дії над матрицями
Задача
6.1.
Обчислити визначник
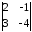 .
.
Розв’язання.
Обчислимо заданий визначник.
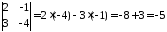 .
.
Задача
6.2.
Обчислити
визначник, використовуючи правило
трикутників
 .
.
Розв’язання.
Обчислимо заданий визначник за формулою 313 (див.схему):
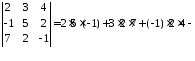
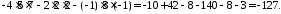
Задача
6.3.
Обчислити визначник, використавши
формулу розкладання визначника за
елементами рядка або стовпця
 .
.
Розв’язання.
Для обчислення цього визначника скористаємось 316. Зручно розкладати даний визначник або за другим рядком, або за третім стовпчиком, оскільки в них є нульовий елемент. Ми використаємо розкладання за другим рядком:

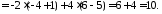
Задача 6.4. Обчислити визначник 4-го порядку:

Розв’язання.
Для зручності обчислень попередньо перетворимо визначник, використовуючи його властивості. Метою цих перетворень є отримання максимальної кількості нулів у рядку або стовпчику, за яким далі розкладатимемо визначник. Спочатку з третього рядка та другого стовпчика винесемо спільні множники, а потім, додавши до другого третій стовпчик, помножений на три, отримаємо максимальну кількість нулів в другому рядку:

Розкладемо визначник за елементами другого рядка, звівши його до визначника третього порядку. Щоб спростити останній, перший рядок додамо до другого, а потім перший рядок віднімемо від третього:
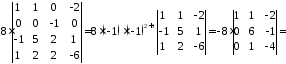

Задача 6.5. Виконати дії над матрицями
1)
 ;
;
2)
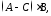
якщо
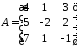 ,
,
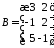 ,
,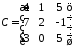 :
:
Розв’язання.

2)
Знайдемо
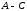 .
Для
цього віднімемо відповідні елементи
заданих матриць:
.
Для
цього віднімемо відповідні елементи
заданих матриць:
 .
.
Далі
виконаємо множення. Оскільки матриці
мають розміри
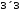 та
та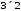 множення можливе, причому матриця,
отримана в результаті, буде мати розміри
множення можливе, причому матриця,
отримана в результаті, буде мати розміри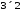 .
.
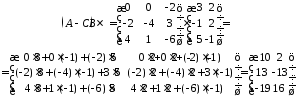
Задача
6.6.
Обчислити
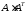 ,
де
,
де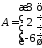 .
.
Розв’язання.
Транспонована
матриця для матриці А
буде мати вигляд
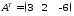 .
Далі виконаємо множення. Оскільки
матриці мають розміри
.
Далі виконаємо множення. Оскільки
матриці мають розміри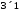 та
та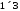 ,
множення можливе, причому матриця,
отримана в результаті, буде мати розміри
,
множення можливе, причому матриця,
отримана в результаті, буде мати розміри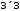 .
.
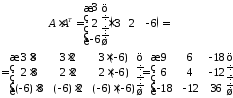
Задача 6.7.
Знайти ранг матриці

Розв’язання.
Обчислимо
визначник матриці
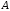 :
:
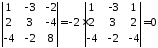 ,
,
оскільки
визначник містить однакові стовпчики.
Отже,
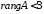 .
Розглянемо визначник другого порядку:
.
Розглянемо визначник другого порядку:
 ,
отже,
,
отже,

Задача
6.8.
Знайти ранг матриці
 ,
використовуючи елементарні перетворення.
,
використовуючи елементарні перетворення.
Розв’язання.
Віднявши від елементів першого рядка елементи другого, а також додавши до елементів третього рядка елементи першого, помножені на (-2), отримаємо:

Слід
помітити, що елементи другого та третього
рядків пропорційні, отже, віднявши від
елементів третього рядка елементи
другого, отримаємо рядок, у якому всі
елементи нульові. Відкинувши цей рядок,
отримаємо матрицю
 .
В ній, наприклад,
.
В ній, наприклад,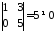 ,
отже,
,
отже,
 .
.
