
- •Глава I. Елементи лінійної та векторної алгебри
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •§23. Приклади розв’язання задач на розкладення векторів по довільному базису і перетворення координат
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
Задачі для самостійної роботи
Обчислити визначник: а)
 ;
б)
;
б) ;
в)
;
в) .
.
Обчислити визначник 1)за правилом трикутника
2) розклавши його за елементами довільного рядка (стовпчика):
а)
 ;.б)
;.б)
 ;
в)
;
в)
Обчислити визначник, попередньо перетворивши його до вигляду, зручного для обчислення:
а)
 ;
б)
;
б)
Знайти
 та
та ,
якщо
,
якщо
Дано дві матриці
 та
та .
Знайти
.
Знайти
 .
.
Знайти добуток
 .
.
Перемножити матриці
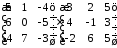 .
.
Знайти ранг кожної з матриць: а)
 ;
б)
;
б)
 ;
;
в)
 ;
г)
;
г) .
.
Питання для повторення
Дії над матрицями, їх властивості.
Обчислення визначників. Теореми про алгебраїчні доповнення.
Властивості визначників.
Ранг матриці, властивості та обчислення.
217Equation Section (Next)§7. Матричний запис системи лінійних алгебраїчних рівнянь. Теорема Кронекера-Капеллі. Дослідження неоднорідних і однорідних систем лінійних рівнянь
Розглянемо довільну систему лінійних рівнянь
 22722\* MERGEFORMAT (.)
22722\* MERGEFORMAT (.)
З цією системою пов’язані наступні матриці:
 23723\* MERGEFORMAT (.)
23723\* MERGEFORMAT (.)
Матриці
 - узгодженні і їх можна перемножити:
- узгодженні і їх можна перемножити:
 24724\* MERGEFORMAT (.)
24724\* MERGEFORMAT (.)
Рівності
722 означають, що відповідні елементи
стовпчиків
 і
і однакові. Тому можна записати
однакові. Тому можна записати
 25725\* MERGEFORMAT (.)
25725\* MERGEFORMAT (.)
Формула
725 є матричним записом неоднорідної
системи 722. У випадку, коли система
однорідна, стовпчик
 складається лише з нулів. Тому матричний
запис однорідної системи має вигляд:
складається лише з нулів. Тому матричний
запис однорідної системи має вигляд:
 26726\* MERGEFORMAT (.)
26726\* MERGEFORMAT (.)
З системою 722, окрім матриць 723 можна пов’язати ще наступну матрицю

Матриця
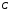 називаєтьсярозширеною
матрицею системи.
називаєтьсярозширеною
матрицею системи.
Має місце наступна теорема, яка є центральною теоремою теорії лінійних систем.
Теорема (Кронекера-Капеллі). Система 722 сумісна тоді і тільки тоді, коли ранг матриці системи дорівнює рангу її розширеної матриці [2].
З цієї теореми випливає, що умова
 27727\* MERGEFORMAT (.)
27727\* MERGEFORMAT (.)
є необхідною і достатньою умовою сумісності системи лінійних алгебраїчних рівнянь.
Застосуємо цю теорему до лінійної неоднорідної системи.
Зрозуміло,
що коли
 то така система несумісна і розв’язків
немає.
то така система несумісна і розв’язків
немає.
Нехай тепер
 28728\* MERGEFORMAT (.)
28728\* MERGEFORMAT (.)
Тоді
якщо
 то система 722 має нескінченну кількість
розв’язків.
то система 722 має нескінченну кількість
розв’язків.
Коли
 ,
система 722 має єдиний розв’язок.
,
система 722 має єдиний розв’язок.
Важливим
випадком є система з квадратною матрицею
 Це означає, що кількість невідомих і
рівнянь в системі однакові. Тоді, щоб
виконувалась рівність 728 і
Це означає, що кількість невідомих і
рівнянь в системі однакові. Тоді, щоб
виконувалась рівність 728 і ,
необхідно, щоб
,
необхідно, щоб
 29729\* MERGEFORMAT (.)
29729\* MERGEFORMAT (.)
729 – умова того, що система 722 з квадратною матрицею має єдиний розв’язок.
У
випадку, коли має місце 728 і
 ,
лінійна система з квадратною матрицею
має безліч розв’язків.
,
лінійна система з квадратною матрицею
має безліч розв’язків.
Нехай
тепер система 722 однорідна. Тоді матриці
 і
і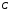 відрізняються на
відрізняються на - стовпчик і тому рівність 728 завжди
має місце. Дійсно, будь-яка однорідна
система має нульовий розв’язок. Коли
- стовпчик і тому рівність 728 завжди
має місце. Дійсно, будь-яка однорідна
система має нульовий розв’язок. Коли ,
цей розв'язок єдиний:
,
цей розв'язок єдиний: .
Якщо
.
Якщо ,
однорідна система має безліч розв’язків,
тобто існують і ненульові розв’язки
системи.
,
однорідна система має безліч розв’язків,
тобто існують і ненульові розв’язки
системи.
Якщо матриця однорідної системи квадратна, то при здійсненні умови 729 така система має єдиний нульовий розв’язок. Щоб у однорідній системі з квадратною матрицею існували ненульові розв’язки, повинна виконуватись умова
 30730\* MERGEFORMAT (.)
30730\* MERGEFORMAT (.)
318Equation Section (Next)§8. Поняття оберненої матриці. Матричний метод розв’язання лінійних алгебраїчних систем. Формули Крамера
Нехай є квадратна матриця
 32832\* MERGEFORMAT (.)
32832\* MERGEFORMAT (.)
Оберненою
для матриці
 називається матриця
називається матриця ,
для якої є вірними рівності
,
для якої є вірними рівності
 , 33833\* MERGEFORMAT (.)
, 33833\* MERGEFORMAT (.)
де
 - одинична матриця розміру
- одинична матриця розміру
Теорема 1. (Про єдність оберненої матриці)
Якщо
у матриці
 існує обернена матриця, то вона єдина.
існує обернена матриця, то вона єдина.
Теореми
про єдиність, як правило, доводяться
методом від протилежного. Припустимо,
що у матриці
 існує дві обернені
існує дві обернені і
і і
і З 833 випливає
З 833 випливає

Цю
рівність справа множимо на
 і перетворюємо отриманий добуток:
і перетворюємо отриманий добуток:



Таким чином, прийшли до того, що обернені матриці мають співпадати, що суперечить зробленому припущенню. А це означає, що зроблене припущення про існування двох різних обернених матриць невірне.
Введемо
поняття невиродженої матриці. Квадратна
матриця називається невиродженою,
якщо її визначник
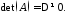
Теорема 2. (Про обернену матрицю).
Кожна
невироджена квадратна матриця
 має єдину обернену матрицю, яка дорівнює
має єдину обернену матрицю, яка дорівнює
 34834\* MERGEFORMAT (.)
34834\* MERGEFORMAT (.)
Матриця
 яка складається з алгебраїчних доповнень
відповідних елементів матриці
яка складається з алгебраїчних доповнень
відповідних елементів матриці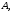 називаєтьсявзаємною
до матриці
називаєтьсявзаємною
до матриці

Єдиність оберненої матриці вже доведено. Залишається показати, що для матриці, яка визначена 834, виконуються рівності 833. Знаходимо, що


Знайдемо
елементи матриці
 :
:

Таким
чином, матриця
 є наступною діагональною матрицею:
є наступною діагональною матрицею:

Тоді
 .
.
Рівність
 доводиться аналогічно і це пропонується
зробити самостійно.
доводиться аналогічно і це пропонується
зробити самостійно.
Таким
чином, формула 834 дійсно визначає
обернену матрицю для невиродженої
квадратної матриці

Обернена матриця дозволяє розв’язувати системи з квадратними матрицями у матричному вигляді. Такий метод розв’язання систем називається матричним.
Нехай
є система лінійних рівнянь з квадратною
матрицею
 визначеною у 832. Матричний запис цієї
системи має вигляд:
визначеною у 832. Матричний запис цієї
системи має вигляд:
 35835\* MERGEFORMAT (.)
35835\* MERGEFORMAT (.)
Нехай
 тоді існує обернена матриця
тоді існує обернена матриця Помножимо 835 на
Помножимо 835 на справа:
справа:
 ,
,
або, згідно 833,
 ,
,
і остаточно
 . 36836\* MERGEFORMAT (.)
. 36836\* MERGEFORMAT (.)
836 – матричний розв’язок системи 835.
Якщо у 836 виконати множення, а саму рівність записати поелементно, то отримаємо відомі формули які мають назву формул Крамера.
Для цього у 836 підставимо 834:
 37837\* MERGEFORMAT (.)
37837\* MERGEFORMAT (.)
Результатом
добутку
 є стовпчик елементи, якого дорівнюють
є стовпчик елементи, якого дорівнюють

Величина
 є розкладенням по елементам
є розкладенням по елементам стовпчика визначника:
стовпчика визначника:
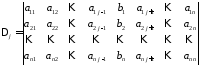 38838\* MERGEFORMAT (.)
38838\* MERGEFORMAT (.)
Легко
бачити, що в кожний визначник
 з 838 утворюється з визначника
з 838 утворюється з визначника внаслідок заміни елементів
внаслідок заміни елементів стовпчика на елементи стовпчика
стовпчика на елементи стовпчика
З 837 знаходимо
 ,
,
звідки випливає
 . 39839\* MERGEFORMAT (.)
. 39839\* MERGEFORMAT (.)
Останні формули і мають назву формул Крамера.
409Equation Section (Next)§9. Задачі на дослідження на сумісність і розв’язування систем лінійних рівнянь. Метод Гауса
Задача 9.1. Дослідити систему лінійних рівнянь на сумісність і у випадку, коли вона має розв’язок, знайти його, використовуючи правило Крамера

Розв’язання.
Обчислимо головний визначник системи.

Отже,
 ,
тому за теоремою Кронекера-Капеллі
система сумісна та має єдиний розв’язок.
,
тому за теоремою Кронекера-Капеллі
система сумісна та має єдиний розв’язок.
Знайдемо допоміжні визначники.



За формулами Крамера 839 знаходимо розв’язок системи:
 .
.
Задача 9.2. Дослідити систему лінійних рівнянь на сумісність і у випадку сумісності знайти розв’язок, використовуючи правило Крамера.

Розв’язання.
Розширена матриця системи має вигляд:
 .
.
Здійснимо елементарні перетворення, додавши до другого рядка перший, помножений на (-2), а до третього - перший, помножений на (-3):
 .
.
Тепер до третього рядка додамо другий, помножений на (-2):
 .
.
Очевидно,
що

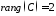 ,
отже,
система сумісна.
,
отже,
система сумісна.
Мінор
 ,
отже, є базисним.
,
отже, є базисним.
Візьмемо
перше та друге рівняння системи, з
коефіцієнтів яких складється базисний
мінор:
 .
.
Тоді за
базисні змінні приймемо
 та
та .
Вільними невідомими будуть
.
Вільними невідомими будуть та
та і
система набуде вигляду:
і
система набуде вигляду:
 .
.
Знайдемо допоміжні визначники системи:
 ;
;
 .
.
В результаті за формулами Крамера маємо:
 .
.
Можна бачити, що формули Крамера доцільно застосовувати, коли система має єдиний розв’язок.
Найбільш зручним і універсальним для практичних цілей є метод Гауса, або метод послідовного виключення невідомих. Його перевагою є те, що одночасно відбуваються дослідження на сумісність і розв’язання системи.
Суть методу Гауса полягає у тому, що за допомогою елементарних перетворень система зводиться до трикутного вигляду, тобто до системи, в якій всі коефіцієнти, розташовані під головною діагоналлю, дорівнюють нулю. З такої системи, приведеної до трикутного вигляду, усі розв’язки знаходяться безпосередньо.
Задача
9.3.
Розв’язати систему за методом Гауса

Розв’язання.
Для
зручності переставимо третє рівняння
на перший рядок. Це рівняння ми вибрали
тому, що з усіх рівнянь у нього найменший
за модулем коефіцієнт при
 .
.
 .
.
Далі
перетворимо друге та третє рівняння
наступним чином. До другого рівняння
додамо перше, помножене на -3;
до третього рівняння додамо перше,
помножене на
 .
Одержимо
.
Одержимо
 .
.
Ми
досягли того, що у другому та третьому
рівняннях коефіцієнти при
 дорівнюють нулю. Тепер до третього
рівняння додамо друге, помножене на
дорівнюють нулю. Тепер до третього
рівняння додамо друге, помножене на .
Маємо
.
Маємо
 .
.
Система записана у трикутному вигляді.
Тепер
із третього рівняння знаходимо
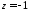 ,
далі з другого рівняння
,
далі з другого рівняння

та, нарешті, з першого рівняння
 .
.
Задача
9.4. Дослідити
систему на сумісність та у випадку
сумісності розв’язати за методом Гауса

Розв’язання.
Замість дій над рівняннями можна здійснювати відповідні перетворення над матрицею системи.
Розширена
матриця системи має вигляд:
 .
.
Знайдемо
ранг
матриці
 ,
здійснивши
елементарні перетворення: додамо до
другого рядка перший,
помножений на (-2), а до третього - перший,
помножений на (-1):
,
здійснивши
елементарні перетворення: додамо до
другого рядка перший,
помножений на (-2), а до третього - перший,
помножений на (-1):
 .
.
Другий та третій рядки отриманої матриці пропорційні, тому:
 .
.
Легко
бачити, що
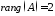 і
і .
.
За
теоремою Кронекера-Капеллі система
сумісна і має безліч розв’язків, так
як
 .
.
Подальша
мета полягає в тому, щоб одержати формули,
за якими всі ці розв’язки можливо
знайти. Для цього назвемо змінну
 вільною змінною і перенесемо доданки
з цією змінною у праві частини обох
рівнянь.
вільною змінною і перенесемо доданки
з цією змінною у праві частини обох
рівнянь.
 .
.
Тепер
виразимо
 та
та через вільну змінну
через вільну змінну .
Маємо:
.
Маємо:
 ,
,
 .
.
Отже,
розв’язки даної системи мають вигляд:
 .
.
Задача 9.5. Розв’язати систему за методом Гауса

Розв’язання.
Приведемо систему до трикутного вигляду. Спочатку для зручності переставимо друге рівняння на перший рядок.

Далі маємо

 ;
;

Останнє рівняння не може виконуватись за будь-яких значень змінної, отже, система несумісна.
Задача 9.6. Розв’язати систему, користуючись методом Гауса:

Розв’язання.
Приведемо розширену матрицю системи до діагонального вигляду:


 .
.
За
теоремою Кронекера-Капеллі система
сумісна, причому кількість базисних
змінних дорівнює
 ,
тоді кількість вільних невідомих
дорівнює
,
тоді кількість вільних невідомих
дорівнює .
Виберемо
будь-який віднінний від нуля мінор
другого порядку отриманої матриці,
наприклад, мінор
.
Виберемо
будь-який віднінний від нуля мінор
другого порядку отриманої матриці,
наприклад, мінор
 .
Його стовпчики (1-й та 2-й стовпчики
матриці) відповідають змінним
.
Його стовпчики (1-й та 2-й стовпчики
матриці) відповідають змінним та
та ,
які візьмемо за базисні (зауважимо, що
для даної системи будь-які два мінори
можуть бути базисними). Запишемо систему
рівнянь, яка відповідає отриманій
розширеній матриці, перенісши вільні
невідомі вправо:
,
які візьмемо за базисні (зауважимо, що
для даної системи будь-які два мінори
можуть бути базисними). Запишемо систему
рівнянь, яка відповідає отриманій
розширеній матриці, перенісши вільні
невідомі вправо:

З останнього рівняння отриманої системи маємо:
 ,
,
тоді
 .
.
Отже, в результаті отримали розв’язки системи:

Задача 9.7. Розв’язати систему лінійних однорідних рівнянь:

Розв’язання.
Особливість
такої системи полягає в тому, що вона
не може бути несумісною. Хоча б один
розв’язок, а саме, нульовий
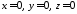 ,
вона має завжди, адже
,
вона має завжди, адже .
Розв’язання такої системи провадиться
повністю аналогічно розв’язанню
неоднорідних систем за методом Гауса.
.
Розв’язання такої системи провадиться
повністю аналогічно розв’язанню
неоднорідних систем за методом Гауса.
Приведемо систему до трикутного вигляду.


Поділимо обидві частини другого рівняння на 2. Далі
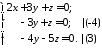
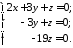
Звідси
випливає, що система має єдиний розв’язок

Задача
9.8.
Знайти обернену матрицю
 для матриці
для матриці
 .
.
Розв’язання.
Обернену матрицю обчислюють за формулою 834.
Спочатку обчислимо визначник заданої матриці.

Оскільки визначник не дорівнює нулю, то дана матриця має обернену. Далі ми знайдемо взаємну матрицю. Для цього обчислимо алгебраїчні доповнення елементів матриці А.
 ,
,
 ,
, ,
,
 ,
,
 ,
,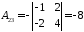 ,
,
 ,
,
 ,
, .
.
Отже, взаємна матриця має вигляд
 .
.
Протранспонувавши її, маємо:
 .
.
Згідно формули 834, одержимо
 .
.
Задача 9.9. Розв’язати систему матричним методом

Розв’язання.
Введемо
у розгляд матриці:
 –
матриця коефіцієнтів,
–
матриця коефіцієнтів,
 –стовпчик
вільних членів та
–стовпчик
вільних членів та
 –стовпчик
невідомих.
–стовпчик
невідомих.
Спочатку обчислимо визначник матриці коефіцієнтів.

Оскільки цей визначник не дорівнює нулю, система сумісна, має єдиний розв’язок і її матриця невироджена.
Далі знайдемо взаємну матрицю. Для цього обчислимо алгебраїчні доповнення елементів матриці А.
 ,
,
 ,
, ,
,
 ,
,
 ,
, ,
,
 ,
,
 ,
, .
.
Отже,
взаємна матриця має вигляд
 .
.
Тепер розв’язок системи знайдемо за формулою 836. Одержимо

Тобто
 .
.
