- •Глава I. Елементи лінійної та векторної алгебри
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •§23. Приклади розв’язання задач на розкладення векторів по довільному базису і перетворення координат
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
Задачі для самостійної роботи
Розв’язати за формулами Крамера:
а) б)
б)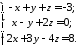 в)
в)
г)

Дослідити системи на сумісність та у випадку сумісності розв’язати методом Гауса:
а) б)
б)
 в)
в)
г)
 д)
д) е)
е)
ж)

Знайти розв’язки систем:
а)
 б)
б) в)
в)
г)
 д)
д)

Побудувати обернену матрицю для кожної з матриць. Зробити перевірку.
 ;
;
 ;
; .
.
Розв’язати системи рівнянь матричним методом:
а)
 б)
б) в)
в) г)
г)
Питання для повторення
Матричний запис системи рівнянь.
Теорема Кронекера-Капеллі.
Обернена матриця, її знаходження.
Формули Крамера.
Метод Гауса.
4110Equation Section (Next)§10. Системи координат на прямій, площині і у просторі. Координати точки
Координати
є засобом для визначення положення
точки за допомогою чисел. Введення
координат точки почнемо з простішого
випадку, а саме прямої. Для цього на
прямій необхідно задати початкову точку
 і додатний напрямок, припустимо, праворуч
від точки
і додатний напрямок, припустимо, праворуч
від точки (Рис. 10.1).
(Рис. 10.1).
|
|
|
Рис. 10.1 |
Окрім
того, необхідно задати одиницю виміру
відстані (масштаб), тобто вказати відрізок
 довжина якого вважається одиничною:
довжина якого вважається одиничною:
Пряма, на якій задано початкову точку, додатний напрямок і масштаб, називається координатною віссю або одновимірною системою координат.
Точка
 називається початком координат. Для
координатних осей використовують
наступні позначення:
називається початком координат. Для
координатних осей використовують
наступні позначення:
Візьмемо
на осі
 довільну точку
довільну точку (Рис.10.1).
(Рис.10.1).
Координатою
точки
 називається число
називається число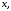 яке дорівнює довжині відрізка
яке дорівнює довжині відрізка якщо точка
якщо точка знаходиться на додатному напрямку осі
і довжині цього відрізка зі знаком
мінус, коли точка знаходиться на
від’ємному напрямку. Тобто
знаходиться на додатному напрямку осі
і довжині цього відрізка зі знаком
мінус, коли точка знаходиться на
від’ємному напрямку. Тобто

Координата
початкової точки
 дорівнює
дорівнює
Якщо
число
 є координатою точки
є координатою точки то це записують так:
то це записують так:
Можна бачити, що кожній точці на координатній осі відповідає єдине дійсне число, а кожному дійсному числу відповідає тільки одна точка на координатній осі.
Таким чином, між дійсними числами і точками координатної осі встановлено взаємно однозначну відповідність. В зв’язку з цим координатну вісь ще називають числовою віссю.
Щоб
ввести системи координат на площині і
у просторі, необхідно ввести поняття
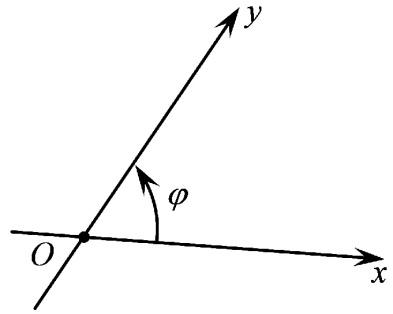
кута між двома впорядкованими осями.
Нехай є дві впорядковані осі, що
перетинаються у точці
 :
: і
і (Рис 10.2).
(Рис 10.2).
|
|
|
Рис. 10.2 |
Кутом
між двома впорядкованими осями
 і
і називається найменший кут
називається найменший кут на який потрібно повернути першу вісь
на який потрібно повернути першу вісь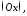 щоб її додатний напрямок збігся з
додатним напрямком другої осі
щоб її додатний напрямок збігся з
додатним напрямком другої осі .
.
Коли обертання відбувається проти хода годинникової стрілки, то кут вважається додатним. Якщо обертання відбувається за ходом годинникової стрілки, то кут вважається від’ємним.
З
визначення можна бачити, що
 .
.
Часто
розглядають обертання тільки в додатному
напрямку осі

Нехай
на площині є дві впорядковані осі
 і
і які утворюють кут
які утворюють кут і перетинаються у точці
і перетинаються у точці (Рис. 10.3). Такі осі складаютьпрямокутну
(декартову)
систему координат на площині. Точка
(Рис. 10.3). Такі осі складаютьпрямокутну
(декартову)
систему координат на площині. Точка
 є початком системи координат.
є початком системи координат.
|
|
|
Рис. 10.3 |
Позначати
систему координат будемо наступним
чином:
 .
.
Система
координат
 називаєтьсяправою,
якщо поворот на найменший кут першої
осі до другої здійснюється проти ходу
годинникової стрілки. У протилежному
випадку система координат називається
лівою. горизонтальну вісь прийнято
називати віссю
абсцис,
вертикальну вісь – віссю
ординат.
Площина, на якій введено систему
координат, називається координатною
площиною. Координатна площина поділяється
осями на чверті, нумерація яких показана
на Рис. 10.3. Визначимо координати точки
в такій системі. Нехай
називаєтьсяправою,
якщо поворот на найменший кут першої
осі до другої здійснюється проти ходу
годинникової стрілки. У протилежному
випадку система координат називається
лівою. горизонтальну вісь прийнято
називати віссю
абсцис,
вертикальну вісь – віссю
ординат.
Площина, на якій введено систему
координат, називається координатною
площиною. Координатна площина поділяється
осями на чверті, нумерація яких показана
на Рис. 10.3. Визначимо координати точки
в такій системі. Нехай
 - довільна точка площини. Проведемо
через точку
- довільна точка площини. Проведемо
через точку перпендикуляри до координатних осей,
через
перпендикуляри до координатних осей,
через позначимо точки перетину перпендикулярів
з осями
позначимо точки перетину перпендикулярів
з осями і
і Точки
Точки єпроекціями
точки
єпроекціями
точки
 на координатні осі.Нехай
точка
на координатні осі.Нехай
точка
 на осі
на осі має координату
має координату а точка
а точка на осі
на осі має координату
має координату Тоді впорядковану пару чисел
Тоді впорядковану пару чисел будемо називатикоординатами
точки
будемо називатикоординатами
точки
 у системі координат
у системі координат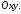 Той факт, що впорядкована пара чисел
Той факт, що впорядкована пара чисел є координатами точки
є координатами точки будемо далі записувати наступним чином:
будемо далі записувати наступним чином:
Таким чином, між точками координатної площини і множиною впорядкованих пар дійсних чисел встановлюється взаємно-однозначна відповідність. Тому систему координат на площині називають двовимірною, а саму координатну площину двовимірним простором.
Окрім
прямокутної декартової у практичній
діяльності, зокрема судноводінні і
навігації, поширена так звана полярна
система координат для визначення
положення точки на площині. Для побудови
такої системи обирається довільна точка
площини
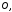 яка називаєтьсяполюсом.
Далі з цієї точки проводиться промінь
яка називаєтьсяполюсом.
Далі з цієї точки проводиться промінь
 який називаєтьсяполярною
віссю
(Рис.10.4)
який називаєтьсяполярною
віссю
(Рис.10.4)
|
|
|
Рис 10.4 |
На
полярній осі задається одиниця виміру
довжини
 Полюс і полярна вісь з заданою одиницею
довжини утворюютьполярну
систему координат
на площині.
Полюс і полярна вісь з заданою одиницею
довжини утворюютьполярну
систему координат
на площині.
Положення
довільної точки
 на
площині визначається наступним чином.
Проводиться промінь
на
площині визначається наступним чином.
Проводиться промінь
 Відрізок
Відрізок
 називається
полярним радіусом, його довжина
позначається
називається
полярним радіусом, його довжина
позначається Кут між полярною віссю і променем
Кут між полярною віссю і променем визначений з врахуванням напряму
повороту , називається полярним кутом
і позначається
визначений з врахуванням напряму
повороту , називається полярним кутом
і позначається Якщо обертання полярної осі здійснюється
проти ходу годинникової стрілки, кут
вважається додатнім, якщо за ходом, то
від'ємним.
Якщо обертання полярної осі здійснюється
проти ходу годинникової стрілки, кут
вважається додатнім, якщо за ходом, то
від'ємним.
Полярними
координатами точки
 називається упорядкована пара чисел
називається упорядкована пара чисел де
де - довжина полярного радіусу,
- довжина полярного радіусу, - величина полярного кута. Те, що ці числа
є полярними координатами точки
- величина полярного кута. Те, що ці числа
є полярними координатами точки ,
записують так:
,
записують так:
Між полярними координатами і точками на площині встановлюється взаємно однозначна відповідність за умов
 або
або

Визначимо зв'язок між полярними і прямокутними координатами точки при умові, що центр прямокутної системи збігається з полюсом полярної системи, а вісь абсцис збігається з полярною віссю (Рис.10.5).
|
|
|
Рис 10.5 |
Нехай
точка
 у прямокутній системі має координати
у прямокутній системі має координати а у полярній
а у полярній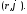 Тоді з співвідношення між гіпотенузою
та катетами прямокутного трикутника
знаходимо
Тоді з співвідношення між гіпотенузою
та катетами прямокутного трикутника
знаходимо
 421042\* MERGEFORMAT (.)
421042\* MERGEFORMAT (.)
Наведені формули виражають декартові координати точки через полярні.
Зворотній
зв'язок за умови
 дається формулами
дається формулами
 431043\* MERGEFORMAT (.)
431043\* MERGEFORMAT (.)
У
просторі прямокутну (декартову) систему
координат утворюють впорядковані трійки
взаємно перпендикулярних осей
 які перетинаються у точці
які перетинаються у точці (Рис.10.6). Точка
(Рис.10.6). Точка називається початком координат.
називається початком координат.
|
|
|
Рис 10.6 |
Система
координат
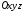 називаєтьсяправою
системою координат
при умові, що з додатного напрямку
третьої осі
називаєтьсяправою
системою координат
при умові, що з додатного напрямку
третьої осі
 поворот на найменший кут першої осі до
другої спостерігається проти ходу
годинникової стрілки. В протилежному
випадку система координат називається
лівою. Простір, в якому введено систему
координат, називається координатним
простором.
поворот на найменший кут першої осі до
другої спостерігається проти ходу
годинникової стрілки. В протилежному
випадку система координат називається
лівою. Простір, в якому введено систему
координат, називається координатним
простором.
 називається
віссю абсцис,
називається
віссю абсцис,
 - віссю ординат,
- віссю ординат, - віссю аплікат.
- віссю аплікат.
Нехай
 - довільна точка простору. Проведемо
через цю точку перпендикулярно до
координатних осей площини (Рис.10.6). Через
- довільна точка простору. Проведемо
через цю точку перпендикулярно до
координатних осей площини (Рис.10.6). Через позначимо точки перетину цих площин з
координатними осями. Нехай точка
позначимо точки перетину цих площин з
координатними осями. Нехай точка має координату
має координату на осі
на осі
 має координату
має координату на осі
на осі
 має координату
має координату на осі
на осі Тоді впорядковану трійку чисел
Тоді впорядковану трійку чисел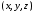 будемо називати координатами точки
будемо називати координатами точки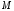 у тривимірній системі координат
у тривимірній системі координат і записувати це наступним чином:
і записувати це наступним чином:
Таким
чином, кожній точці простору відповідає
у системі координат впорядкована трійка
чисел. Кожній впорядкованій трійці
чисел відповідає точка простору. Між
трійками чисел і точками координатного
простору встановлюється взаємно
однозначна відповідність. Множини усіх
впорядкованих трійок чисел називається
тривимірним
простором
і позначається

Поняття простору може бути узагальнено.
Розглянемо
множину усіх впорядкованих сукупностей
з
 дійсних чисел
дійсних чисел
Множина
усіх можливих сукупностей з
 дійсних чисел
дійсних чисел називається
називається - вимірним простором,
або простором
- вимірним простором,
або простором
 вимірів і позначається
вимірів і позначається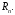
Кожна
впорядкована сукупність з
 дійсних чисел називається точкою
дійсних чисел називається точкою - вимірного простору і позначається
- вимірного простору і позначається Числа
Числа називаються координатами точки
називаються координатами точки - вимірного простору.
- вимірного простору.
Точку
 у прямокутній системі координат
у прямокутній системі координат можна визначити не тільки декартовими
координатами, а ще й циліндричними і
сферичними. Нехай
можна визначити не тільки декартовими
координатами, а ще й циліндричними і
сферичними. Нехай - проекція точки
- проекція точки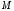 на площину
на площину (Рис. 10.7).
(Рис. 10.7).
|
|
|
Рис 10.7 |
Ця
точка у полярній системі координат з
полюсом
 і полярною віссю
і полярною віссю має координати
має координати Тоді впорядковану трійку чисел
Тоді впорядковану трійку чисел називаютьциліндричними
координатами точки
називаютьциліндричними
координатами точки
 і записують це так:
і записують це так: Зв'язок між декартовими координатами
точки
Зв'язок між декартовими координатами
точки і її циліндричними координатами, як
можна бачити з Рис.10.7 і формул 1042,
встановлюється формулами
і її циліндричними координатами, як
можна бачити з Рис.10.7 і формул 1042,
встановлюється формулами
 441044\* MERGEFORMAT (.)
441044\* MERGEFORMAT (.)
Для
введення сферичних координат точки
 знову розглядається її проекція
знову розглядається її проекція на площину
на площину і полярні координати точки
і полярні координати точки (Рис.10.7) і проводиться площина через
точку
(Рис.10.7) і проводиться площина через
точку і вісь аплікат
і вісь аплікат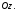 Нехай відстань від початку координат
до точки
Нехай відстань від початку координат
до точки дорівнює
дорівнює а кут між віссю
а кут між віссю і променем
і променем дорівнює
дорівнює Тоді впорядковану трійку чисел
Тоді впорядковану трійку чисел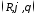 називаютьсферичними
координатами точки
називаютьсферичними
координатами точки
 і записують це так:
і записують це так: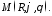 Щоб встановити зв'язок між прямокутними
і сферичними координатами точки
Щоб встановити зв'язок між прямокутними
і сферичними координатами точки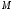 з
з знаходимо
знаходимо

Остаточно згідно 1042 приходимо до формул:
 451045\* MERGEFORMAT (.)
451045\* MERGEFORMAT (.)
4611Equation Section (Next)§11. Скалярні та векторні величини. Поняття вектора. Лінійні операції з векторами у геометричній формі і їх властивості
Усі величини можуть бути поділені на скалярні та векторні. Скалярні величини повністю визначаються їх числовими даними. Наприклад, довжина, густина, маса, температура тощо.
Векторною називається величина, яка визначається не тільки числовим значенням, а ще й напрямком. Геометрично векторні величини зображуються за допомогою векторів, під якими розуміється направлений відрізок.
Вектором
 називається направлений відрізок
називається направлений відрізок з початковою точкою
з початковою точкою і кінцевою точкою
і кінцевою точкою (Рис.11.1).
(Рис.11.1).
|
|
|
Рис 11.1 |
Як можна бачити з визначення, напрямок вектора задається від початкової точки до кінцевої. Коли неважливо, у якій саме точці має початок і кінець вектор, він позначається однією буквою:

Довжину відрізка, на якому розміщується вектор, називають модулем або довжиною вектора і позначають

Будь-які
два вектори
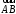 і
і називаютьсярівними,
якщо вони мають однакові довжини
називаютьсярівними,
якщо вони мають однакові довжини
 і однаковий напрямок (Рис.11.1).
Тобто у цьому випадку
і однаковий напрямок (Рис.11.1).
Тобто у цьому випадку
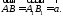 Геометрично це означає, що рівні вектори
збігаються при паралельному перенесенні.
Геометрично це означає, що рівні вектори
збігаються при паралельному перенесенні.
Якщо
початкова і кінцева точки вектора
збігаються, то вектор має нульову
довжину. Такий вектор називається
нульовим,
або нуль-вектором і позначається
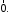 Вектор
Вектор такий, що
такий, що ,
називаєтьсяодиничним
вектором.
,
називаєтьсяодиничним
вектором.
В залежності від того, як вектори розміщуються у просторі, відрізняються колінеарні і компланарні.
Вектори
 що знаходяться на одній або на паралельних
прямих, називаютьсяколінеарними.
що знаходяться на одній або на паралельних
прямих, називаютьсяколінеарними.
Вектори
 що знаходяться у одній або паралельних
площинах, називаютьсякомпланарними.
що знаходяться у одній або паралельних
площинах, називаютьсякомпланарними.
Над векторами у геометричній формі можна здійснювати такі операції як множення на число і додавання. Ці операції називаються лінійними операціями над векторами.
Добутком
вектора
 на число (скаляр)
на число (скаляр) називається вектор
називається вектор що визначається наступними умовами:
що визначається наступними умовами:

вектори
 і
і колінеарні і спрямовані однаково при
колінеарні і спрямовані однаково при і спрямовані у протилежних напрямках
коли,
і спрямовані у протилежних напрямках
коли,
Добутком
будь-якого вектора на
 є нуль-вектор:
є нуль-вектор:

Вектор
 що має однакову з
що має однакову з довжину і протилежний напрямок.
називаєтьсяпротилежним
до
довжину і протилежний напрямок.
називаєтьсяпротилежним
до

Сумою
двох векторів
 і
і є третій вектор
є третій вектор ,
який будується згідно з правилом
трикутника або правилом паралелограма
(Рис. 11.2):
,
який будується згідно з правилом
трикутника або правилом паралелограма
(Рис. 11.2):
|
|
|
Рис 11.2 |
Правило
трикутника очевидно поширюється на
будь-яку кількість векторних доданків
 (Рис. 11.3).
(Рис. 11.3).
|
|
|
Рис 11.3 |
За допомогою поняття протилежного вектора можна ввести і поняття різниці двох векторів
 .
.
Лінійні операції над векторами мають наступні властивості:
 (комутативність
додавання);
(комутативність
додавання); (асоціативність
додавання).
(асоціативність
додавання).
Для
будь-якого
 :
:
 ;
; ;
; ;
; (асоціативність
добутку на число);
(асоціативність
добутку на число); (дистрибутивність
відносно додавання векторів);
(дистрибутивність
відносно додавання векторів);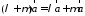 (дистрибутивність
відносно додавання скалярів).
(дистрибутивність
відносно додавання скалярів).
4712Equation Section (Next)§12. Проекція вектора на вісь і її властивості
Розглянемо
у просторі деяку вісь
 і вектор
і вектор (Рис.12.1).
(Рис.12.1).
Кутом
між вектором
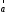 та віссю
та віссю називається найменший кут, на який
потрібно повернути вісь проти ходу
годинникової стрілки, щоб її напрямок
співпав з напрямком вектора:
називається найменший кут, на який
потрібно повернути вісь проти ходу
годинникової стрілки, щоб її напрямок
співпав з напрямком вектора:
|
|
|
Рис 12.1 |
Очевидно,
при такому визначенні значення кута
між вектором та віссю знаходиться у
межах

Проекцією
вектора
 на вісь
на вісь називається число, яке дорівнює добутку
довжини вектора на косинус кута між
вектором та віссю:
називається число, яке дорівнює добутку
довжини вектора на косинус кута між
вектором та віссю:
 481248\* MERGEFORMAT (.)
481248\* MERGEFORMAT (.)
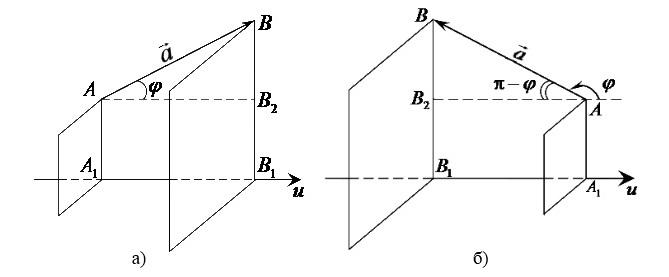
Встановимо геометричний зміст поняття проекції.
|
|
|
Рис 12.2 |
Для
цього через початок і кінець вектора
проведемо площини перпендикулярно до
осі (Рис.12.2)
і точки перетину цих площин з віссю
позначимо
 В залежності від кута між вектором та
віссю з
В залежності від кута між вектором та
віссю з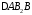 знаходимо
знаходимо
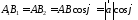
або

Але тоді згідно 1248

де знак
 відповідає додатному значенню
відповідає додатному значенню ,
а знак
,
а знак від'ємному значенню
від'ємному значенню
Остання
рівність встановлює наступний геометричний
зміст поняття проекції вектора на вісь.
Проекція вектора
 на вісь з точністю до знака дорівнює
довжині відрізка, що відтинається на
осі площинами, що проходять перпендикулярно
до неї через точки
на вісь з точністю до знака дорівнює
довжині відрізка, що відтинається на
осі площинами, що проходять перпендикулярно
до неї через точки і
і Ця довжина береться зі знаком плюс, коли
косинус кута між вектором та віссю
додатний і зі знаком мінус, якщо цей
косинус від'ємний.
Ця довжина береться зі знаком плюс, коли
косинус кута між вектором та віссю
додатний і зі знаком мінус, якщо цей
косинус від'ємний.
Розглянемо інші властивості поняття проекції.
Рівні вектори мають рівні проекції:

Для будь-якого скаляра

 491249\* MERGEFORMAT (.)
491249\* MERGEFORMAT (.)
При
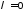 рівність очевидна. Нехай
рівність очевидна. Нехай і
і Якщо
Якщо то
то

Коли
 то
то

Для будь-яких векторів
 і
і
 501250\* MERGEFORMAT (.)
501250\* MERGEFORMAT (.)
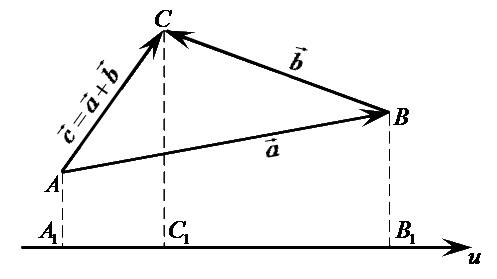
Для доведення цієї властивості використаємо геометричний зміст поняття проекції (Рис. 12.3)
|
|
|
Рис 12.3 |
Згідно з зображеним випадком
 ,
,
але
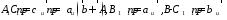 ,
,
звідки випливає 1250.
Нехай
 -деякі
вектори, а
-деякі
вектори, а -деякі числа. Вираз
-деякі числа. Вираз називаєтьсялінійною
комбінацією
векторів
називаєтьсялінійною
комбінацією
векторів
 .
Узагальненням (10.2) і (10.3) є наступна
властивість.
.
Узагальненням (10.2) і (10.3) є наступна
властивість.
Для будь-якої лінійної комбінації векторів має місце рівність:
 511251\* MERGEFORMAT (.)
511251\* MERGEFORMAT (.)
Якщо вектор та вісь перпендикулярні, то

Зауважимо,
що для ненульового вектора
 рівність нулю проекції є необхідною і
достатньою умовою перпендикулярності
вектора та осі.
рівність нулю проекції є необхідною і
достатньою умовою перпендикулярності
вектора та осі.
Аналогічно
можна ввести поняття проекції вектора
 на інший вектор
на інший вектор .
Під нею розуміється число, яке дорівнює
.
Під нею розуміється число, яке дорівнює
 521252\* MERGEFORMAT (.)
521252\* MERGEFORMAT (.)
де
 -кут
між векторами
-кут
між векторами та
та .
.
Очевидно, що властивості проекції вектора на інший вектор співпадають з властивостями проекції вектора на вісь.
5313Equation Section (Next)§13. Координати вектора. Визначення вектора за його координатами. Лінійні операції над векторами у координатній формі
Нехай
у просторі є система координат
 і довільний вектор
і довільний вектор .
Через
.
Через позначимо кути, що утворює вектор з
координатними осями:
позначимо кути, що утворює вектор з
координатними осями:

|
|
|
Рис 13.1 |
Введемо
до розгляду проекції вектора
 на координатні вісі:
на координатні вісі:
 ,
,
 ,
,
Впорядковану
трійку чисел
 ,
які є проекціями вектора
,
які є проекціями вектора на відповідні координатні вісі, називаютькоординатами
вектора
на відповідні координатні вісі, називаютькоординатами
вектора
 у прямокутній системі координат
у прямокутній системі координат .
.
Те,
що вектор
 має координати
має координати ,
будемо
записувати так:
,
будемо
записувати так:

Згідно визначення проекції та 1248 знаходимо:
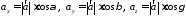 541354\* MERGEFORMAT (.)
541354\* MERGEFORMAT (.)
Таким чином, якщо відомі довжина та напрямок вектора, то його координати однозначно визначаються формулами 1354. Доведемо, що за координатами вектора можна знайти його довжину і напрямок.
Нехай
відомі координати вектора
 .
Побудуємо на цьому векторі як на діагоналі
(Рис. 13.1) прямокутний паралелепіпед.
Тоді знаходимо:
.
Побудуємо на цьому векторі як на діагоналі
(Рис. 13.1) прямокутний паралелепіпед.
Тоді знаходимо:

Аналогічно

Для діагоналі прямокутного паралелепіпеду має місце формула
 .
.
Звідси випливає
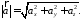 551355\* MERGEFORMAT (.)
551355\* MERGEFORMAT (.)
Отже,
якщо є координати вектора , то його
довжина визначається формулою 1355.
Напрямок вектора визначається кутами,
які він утворює з координатними осями.
Якщо
 ,
то з 1354
знаходимо:
,
то з 1354
знаходимо:
 561356\* MERGEFORMAT (.)
561356\* MERGEFORMAT (.)
Ці
формули дозволяють однозначно визначити
кути між вектором і координатними осями,
при умові
 Косинуси кутів, що утворює вектор з
осями координат, називаються йогонапрямними
косинусами.
Згідно з 1356 маємо:
Косинуси кутів, що утворює вектор з
осями координат, називаються йогонапрямними
косинусами.
Згідно з 1356 маємо:

Таким чином,
 571357\* MERGEFORMAT (.)
571357\* MERGEFORMAT (.)
Отже кути, що утворює вектор з осями координат, не можуть бути довільними. Вони мають бути такими, щоб виконувалась рівність 1357.
Нехай
є два вектори, які задані своїми
координатами:
 і
і .
Очевидно, оскільки рівні вектори мають
рівні проекції, то, якщо
.
Очевидно, оскільки рівні вектори мають
рівні проекції, то, якщо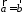 ,
то і
,
то і .
.
З
формул 1355, 1356 випливає, що при рівних
координатах вектори
 та
та мають однакові довжину і напрямок, тобто
є рівними. Таким чином, будь-який вектор
однозначно визначається своїми
координатами.
мають однакові довжину і напрямок, тобто
є рівними. Таким чином, будь-який вектор
однозначно визначається своїми
координатами.
Розглянемо, що відбувається з координатами векторів при здійсненні лінійних операцій.
Нехай
 - довільне число, тоді згідно 1249
- довільне число, тоді згідно 1249



Це означає, що
 . 581358\* MERGEFORMAT (.)
. 581358\* MERGEFORMAT (.)
Таким чином, при множенні вектора на число на це число множиться кожна його координата.
Для
суми
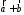 за формулою 1250 знаходимо
за формулою 1250 знаходимо


 ,
,
а це означає, що
 . 591359\* MERGEFORMAT (.)
. 591359\* MERGEFORMAT (.)
Отже, додаванню векторів відповідає додавання їх відносних координат.
Формули
1358, 1359 узагальнюються на випадок
лінійної комбінації довільної системи
векторів
 :
:
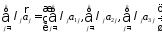 601360\* MERGEFORMAT (.)
601360\* MERGEFORMAT (.)
Формули 1358-1360 встановлюють правила дій над векторами у координатній формі.
6114Equation Section (Next)§14. Розкладання вектора по базисним векторам (ортам) системи координат. Визначення вектора координатами початку і кінця. Обчислення відстані між двома точками у просторі
З
кожною просторовою системою координат можна пов’язати три вектора
можна пов’язати три вектора ,
що мають довжину
,
що мають довжину і спрямовані так само, як вісі
і спрямовані так само, як вісі відповідно (Рис.14.1).
Вектори
відповідно (Рис.14.1).
Вектори
 називаютьсяортами
координатних осей
називаютьсяортами
координатних осей
 ,
або базисними векторами системи координат
,
або базисними векторами системи координат .
.
|
|
|
Рис 14.1 |
Базисні вектори системи координат мають координати

Має місце теорема.
Теорема.
Довільний вектор
 може бути поданий у вигляді
може бути поданий у вигляді
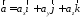 621462\* MERGEFORMAT (.)
621462\* MERGEFORMAT (.)
Дійсно, згідно з 1360:

Буде вірною і обернена теорема.
Теорема.
Якщо для вектора
 має місце подання 1462, то
має місце подання 1462, то .
.
Дійсно, згідно властивостям проекції

Аналогічно,
 ,
, .
.
Кожній
точці простору
 можна поставити у відповідність вектор
можна поставити у відповідність вектор ,
який називаєтьсярадіус-вектором
цієї точки.
,
який називаєтьсярадіус-вектором
цієї точки.
Має місце теорема.
Теорема.
Якщо
 ,
то у цій же системі координат її
радіус-вектор
,
то у цій же системі координат її
радіус-вектор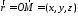 .
.
Розглядаємо
проекції
 на координатні вісі (рис.15.1):
на координатні вісі (рис.15.1):
 .
.
Тому
 .
.
Теорема.
Нехай
 і
і ,
, .
Тоді різниці
.
Тоді різниці дорівнюють відповідним координатам
вектора
дорівнюють відповідним координатам
вектора .
.
Розглянемо
радіус вектори точок
 і
і :
: ,
, .
.
З
векторного трикутника
 (рис 14.2)
(рис 14.2)
 .
.
 631463\* MERGEFORMAT (.)
631463\* MERGEFORMAT (.)
|
|
|
Рис 14.2 |
Формула
1463 показує, що координати будь-якого
вектора
 дорівнюють різницям відповідних
координат його кінця і початку.
дорівнюють різницям відповідних
координат його кінця і початку.
Оскільки
відстань між точками
 і
і дорівнює
довжині вектора
дорівнює
довжині вектора ,
то маємо формулу для обчислення відстані
між двома точками, заданими своїми
координатами:
,
то маємо формулу для обчислення відстані
між двома точками, заданими своїми
координатами:
 641464\* MERGEFORMAT (.)
641464\* MERGEFORMAT (.)
6515Equation Section (Next)§15. Поділ відрізка у даному відношенні. Відшукання координат центра тяжіння системи матеріальних точок.
Поняття векторів та їх координат дозволяють легко розв’язувати такі практично важливі задачі, як поділ відрізка у даному відношенні і обчислення координат центра тяжіння системи матеріальних точок.
Задача
поділу відрізка у заданому відношенні
формулюється наступним чином. У деякій
системі координат
 задані дві точки
задані дві точки і
і .
Необхідно знайти координати точки
.
Необхідно знайти координати точки ,
яка ділить відрізок
,
яка ділить відрізок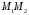 у заданому відношенні
у заданому відношенні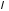 :
:
 661566\* MERGEFORMAT (.)
661566\* MERGEFORMAT (.)
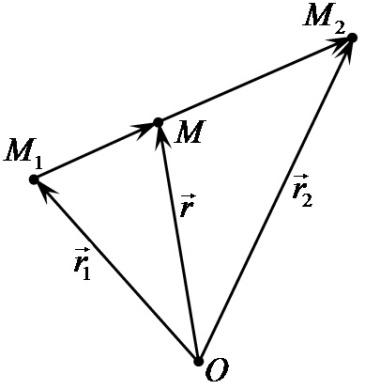
Для
розв’язання позначимо координати точки
 і розглянемо радіус-вектори (Рис.16.1):
і розглянемо радіус-вектори (Рис.16.1):
 .
.
|
|
|
Рис 15.1 |
Оскільки
вектори
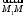 і
і колінеарні і однаково спрямовані, то з
1566 випливає рівність:
колінеарні і однаково спрямовані, то з
1566 випливає рівність:

Але
 ,
тоді
,
тоді

Звідси знаходимо
 671567\* MERGEFORMAT (.)
671567\* MERGEFORMAT (.)
Формула
1567 знаходить радіус-вектор невідомої
точки
 і є векторним розв’язком задачі про
поділ відрізка. Запис 1567 у координатній
формі дає такі формули для координат:
і є векторним розв’язком задачі про
поділ відрізка. Запис 1567 у координатній
формі дає такі формули для координат:
 681568\* MERGEFORMAT (.)
681568\* MERGEFORMAT (.)
Отримані
формули 1568 можна застосувати до
розв’язання задачі відшукання центра
тяжіння
 системи матеріальних точок
системи матеріальних точок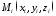 з масами
з масами .
.
Спочатку
визначимо точку
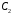 ,
яка є центром тяжіння двох точок
,
яка є центром тяжіння двох точок і
і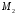 .
Ця точка знаходиться на відрізку
.
Ця точка знаходиться на відрізку і розділяє його на відрізки обернено
пропорційно масам, зосередженим у цих
точках
і розділяє його на відрізки обернено
пропорційно масам, зосередженим у цих
точках

Нехай
 ‑
радіус-вектор точки
‑
радіус-вектор точки .
Тоді з 1567 при
.
Тоді з 1567 при знаходимо
знаходимо
 691569\* MERGEFORMAT (.)
691569\* MERGEFORMAT (.)
Тепер
радіус-вектор точки тяжіння системи
трьох точок
 знаходиться за 1569, у припущенні, що в
точці
знаходиться за 1569, у припущенні, що в
точці зосереджена маса
зосереджена маса ,
а у точці
,
а у точці знаходиться маса
знаходиться маса :
:

Після
підстановки значення
 з 1569 і перетворень отримаємо наступну
формулу для радіус-вектора центра
тяжіння системи трьох точок:
з 1569 і перетворень отримаємо наступну
формулу для радіус-вектора центра
тяжіння системи трьох точок:
 701570\* MERGEFORMAT (.)
701570\* MERGEFORMAT (.)
З
огляду на формули 1569, 1570 можна висунути
припущення, що радіус-вектор точки
 ,
яка є центром тяжіння системи
,
яка є центром тяжіння системи матеріальних точок, знаходиться за
формулою:
матеріальних точок, знаходиться за
формулою:
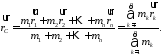 711571\* MERGEFORMAT (.)
711571\* MERGEFORMAT (.)
Строге доведення цієї формули можна здійснити згідно з методом математичної індукції. Формула 1571 може бути переписана також і у координатній формі:
 721572\* MERGEFORMAT (.)
721572\* MERGEFORMAT (.)
7316Equation Section (Next)§16. Задачі на обчислення координат точок в різних системах. Дії над векторами в координатній формі
Задача
16.1.
Знайти
координати середини відрізка
 ,
якщо
,
якщо ,
а
,
а .
.
Розв’язання.
Нехай
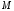 -середина
-середина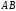 ,
тоді, згідно 1568 при
,
тоді, згідно 1568 при маємо:
маємо:
 .
.
Задача
16.2.
Знайти
координати точок
 та
та ,
які ділять відрізок
,
які ділять відрізок на три рівні частини, якщо
на три рівні частини, якщо ,
а
,
а .
.
Розв’язання.
Спершу
знайдемо координати точки
 .
Для неї згідно 1566
.
Для неї згідно 1566 .
Використовуючи 1568, одержимо:
.
Використовуючи 1568, одержимо:
 .
.
Аналогічно
обчислимо координати точки
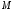 ,
для якої
,
для якої :
:
 .
.
Отже,
 ,
,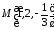 .
.
Задача
16.3.
У точках
 ,
, ,
, розміщено матеріальні точки з масами
60, 40 і 100 г. Знайти центр мас цієї системи.
розміщено матеріальні точки з масами
60, 40 і 100 г. Знайти центр мас цієї системи.
Розв’язання.
Скористаємось 1572:
 ;
;

Отже,
центром мас є точка
 .
.
Задача
16.4.
Знайти
циліндричні координати точки за її
прямокутними координатами:
 .
.
Розв’язання.
Згідно формул зв’язку 1043 маємо:

Отже,
за формулою 1044 отримали циліндричні
координати точки:
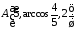 .
.
Задача
16.5. Знайти
полярні координати точки
 ,
якщо полюс співпадає з початком координат,
а полярна вісь - з додатнім напрямом осі
абсцис.
,
якщо полюс співпадає з початком координат,
а полярна вісь - з додатнім напрямом осі
абсцис.
Розв’язання.
За 1043 отримаємо:
 ,
таким чином,
,
таким чином,
 .
.
Задача
16.6.
Знайти декартові координати точки
 ,
якщо полюс співпадає з початком координат,
а полярна вісь напрямлена по осі абсцис.
,
якщо полюс співпадає з початком координат,
а полярна вісь напрямлена по осі абсцис.
Розв’язання.
Для знаходження декартових координат скористаємось формулами зв’язку 1042, згідно з якими
 .
.
Отримали
 .
.
Задача
16.7.
Знайти
координати середини відрізка
 ,
якщо
,
якщо ,
а
,
а .
.
Розв’язання.
Спочатку знайдемо ці точки в декартовій системі координат (див.1042):
 ;
;
 .
.
Обчислимо
координати середини
 :
:
 .
.
Задача
16.8.
Знайти
відстань між точками
 та
та .
.
Розв’язання.
Скористаємось формулою 1464, попередньо визначивши координати даних точок в декартовій системі:
 ;
; .
.
Тепер

Зауваження.
Для
знаходження відстані між точками
 та
та зручно також скористатися теоремою
косинусів, за якою
зручно також скористатися теоремою
косинусів, за якою
 .
.
Задача
16.9.
Знайти прямокутні координати точки, що
знаходиться на сфері радіуса 3 знаючи
широту точки
 і
довготу
і
довготу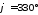 .
Центр сфери співпадає з початком
прямокутної системи.
.
Центр сфери співпадає з початком
прямокутної системи.
Розв’язання.
Задано
точку в сферичній системі координат:
 .
За формулами 1045 переходимо до прямокутних
координат:
.
За формулами 1045 переходимо до прямокутних
координат:

Отже,
в декартовій системі
 .
.
Задача
16.10.
Знайти
модуль вектора
 та його напрямні косинуси, якщо
та його напрямні косинуси, якщо
 ,
,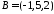 .
.
Розв’язання.
Спочатку знайдемо координати вектора 1463:
 .
.
Довжина
(модуль) вектора
 знаходиться згідно 1355:
знаходиться згідно 1355:
 .
.
Напрямні
косинуси 1356 вектора
 мають вигляд:
мають вигляд:
 .
.
Задача
16.11.
Вектор складає з осями
 та
та кути
кути та
та відповідно. Який кут він складає з віссю
відповідно. Який кут він складає з віссю ?
?
Розв’язання.
Використаємо рівність 1357. Тоді
 ,
,
тобто
 ,
значить
,
значить або
або .
.
Задача
16.12.
Дано два вектори
 та
та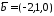 .
Знайти координати векторів:
.
Знайти координати векторів:
1) ;
;
2) .
.
Розв’язання.
За правилами дій над векторами в координатній формі 1358-1360 маємо:
1)
координати
 ,
тоді
,
тоді
 .
.
2)
координати
 ,
тоді
,
тоді
 .
.