
- •Глава I. Елементи лінійної та векторної алгебри
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •§23. Приклади розв’язання задач на розкладення векторів по довільному базису і перетворення координат
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
Задачі для самостійної роботи
Знайти полярні координати точки
 ,
якщо полюс співпадає з початком
координат, а полярна вісь - з додатнім
напрямом осі абсцис.
,
якщо полюс співпадає з початком
координат, а полярна вісь - з додатнім
напрямом осі абсцис.Знайти декартові координати точки
 ,
якщо полюс співпадає з початком
координат, а полярна вісь напрямлена
по осі абсцис.
,
якщо полюс співпадає з початком
координат, а полярна вісь напрямлена
по осі абсцис.Знайти прямокутні координати точки, що знаходиться на сфері радіуса 5 знаючи широту точки
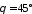 і
довготу
і
довготу .
Центр сфери співпадає з початком
прямокутної системи.
.
Центр сфери співпадає з початком
прямокутної системи.Знайти циліндричні координати точки за її прямокутними координатами:
 .
.Знайти координати середини відрізка
 ,
якщо
,
якщо ,
а
,
а
Дано координати точок:
 ,
, .
Знайти координати трьох точок, які
поділяють відрізок
.
Знайти координати трьох точок, які
поділяють відрізок на три рівні частини.
на три рівні частини.Знайти відстань між точками
 та
та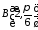
Дано координати вектора
 :
:
 .
Знайти координату
.
Знайти координату ,
якщо відомо, що
,
якщо відомо, що .
.Визначити початок вектора
 ,
якщо його кінець співпадає з точкою
,
якщо його кінець співпадає з точкою
Дано
 та
та .
Знайти модуль суми та різниці цих
векторів.
.
Знайти модуль суми та різниці цих
векторів.Обчислити напрямні косинуси вектора
 ,
якщо
,
якщо та
та .
.З’ясувати, чи може вектор становити з координатними осями кути
 .
.Знайти координати центра ваги трикутника
 :
: ,
, ,
, .
.Дано координати вершин трикутника:
 .
Показати, що трикутник
.
Показати, що трикутник правильний.
правильний.
Питання для повторення
Декартова, полярна, циліндрична, сферична симтеми координат. Формули зв’язку між ними.
Поняття вектора. Лінійні операції з векторами та їх властивості. Проекція вектора на вісь.
Розкладання вектора по базисним векторам (ортам) системи координат. Обчислення відстані між двома точками у просторі.
Поділ відрізка у заданому відношенні. Центр тяжіння системи матеріальних точок.
7417Equation Section (Next)§17. Скалярний добуток векторів і його основні властивості
Для
введення операції скалярного множення
векторів попередньо необхідно визначити
кут між векторами. Нехай два вектора
 і
і мають початок у одній точці. Кутом між
векторами
мають початок у одній точці. Кутом між
векторами і
і розуміється найменший кут, на який
потрібно повернути перший вектор, щоб
його напрямок співпадав з напрямком
другого вектора (Рис.17.1).
розуміється найменший кут, на який
потрібно повернути перший вектор, щоб
його напрямок співпадав з напрямком
другого вектора (Рис.17.1).
|
|
|
Рис 17.1 |

Згідно
з таким визначенням виконується
нерівність:
 або
або .
.
Також має місце співвідношення
 або
або
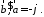
Скалярним
добутком
двох векторів
 і
і називається число, яке дорівнює добутку
модулів цих векторів, помножене на
косинус кута, що утворюють ці вектори:
називається число, яке дорівнює добутку
модулів цих векторів, помножене на
косинус кута, що утворюють ці вектори:
 751775\* MERGEFORMAT (.)
751775\* MERGEFORMAT (.)
З визначення та формули 1775 випливають наступні властивості цієї дії:
Операція векторного добутку є комутативною:
 .
.
Дійсно,
 .
.
Асоціативність відносно додавання

Для будь-якого дійсного числа


Скалярний добуток вектора самого на себе (скалярний квадрат вектора) дорівнює квадрату його довжини:

Дійсно,

Необхідна і достатня умови перпендикулярності двох векторів.
Для
того, щоб два ненульових вектори
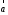 і
і були перпендикулярні, необхідно і
достатньо, щоб їх скалярний добуток
дорівнював нулю:
були перпендикулярні, необхідно і
достатньо, щоб їх скалярний добуток
дорівнював нулю:
 . 761776\* MERGEFORMAT (.)
. 761776\* MERGEFORMAT (.)
Доведення
необхідності.
Нехай
 і
і і вони перпендикулярні. Слід довести
рівність
1776.
Оскільки вектори перпендикулярні, то
і вони перпендикулярні. Слід довести
рівність
1776.
Оскільки вектори перпендикулярні, то
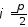 або
або і
і Тоді
з 1775 знаходимо:
Тоді
з 1775 знаходимо: .
.
Доведення
достатності.
Нехай виконується
1776.
Але
тоді
 Оскільки
Оскільки і
і ,
то остання рівність можлива тільки у
випадку, коли
,
то остання рівність можлива тільки у
випадку, коли Згідно з визначенням кута між векторами,
це означає, що
Згідно з визначенням кута між векторами,
це означає, що або
або тобто вектори перпендикулярні.
тобто вектори перпендикулярні.
Скалярні добутки базисних векторів системи координат.
Нехай
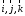 ‑ базисні вектори системи координат
‑ базисні вектори системи координат .
Тоді
.
Тоді
 771777\* MERGEFORMAT (.)
771777\* MERGEFORMAT (.)
Координатна форма скалярного добутку.
Якщо
вектори
 і
і задано в системі координат
задано в системі координат то їх скалярний добуток дорівнює
то їх скалярний добуток дорівнює
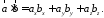 781778\* MERGEFORMAT (.)
781778\* MERGEFORMAT (.)
Для доведення формули 1778 слід скористатись розкладенням векторів по базисним векторам системи координат (12.1):
 791779\* MERGEFORMAT (.)
791779\* MERGEFORMAT (.)
Тоді

При виведенні цієї формули суттєво використовувалися формули 1777.
Скалярний добуток може бути застосований до розв’язання наступних практичних задач:
Обчислення кута між двома ненульовими векторами.
Нехай
вектори 1779 утворюють кут
 і
і ,
, .
Тоді з 1775, 1778 і (11.2) знаходимо
.
Тоді з 1775, 1778 і (11.2) знаходимо
 801780\* MERGEFORMAT (.)
801780\* MERGEFORMAT (.)
Формула 1780 дозволяє знайти косинус кута між будь-якими векторами, а отже, визначити і сам цей кут.
За допомогою 1780 умова перпендикулярності векторів теж може бути записана у координатному вигляді:

Обчислення роботи сили.
Нехай
матеріальна точка здійснює переміщення
 з точки
з точки у точку
у точку під дією сили
під дією сили Тоді робота сили
Тоді робота сили по переміщенню цієї точки дорівнює
по переміщенню цієї точки дорівнює
 811781\* MERGEFORMAT (.)
811781\* MERGEFORMAT (.)
Обчислення проекції вектора на вектор.
Дійсно, з 1775 знаходимо:
 ,
,
тоді
 821782\* MERGEFORMAT (.)
821782\* MERGEFORMAT (.)
8318Equation Section (Next)§18. Векторний добуток векторів і його основні властивості
Якщо
розглядати впорядковані трійки
некомпланарних векторів
 то їх можна поділити на такі, що мають
праву і ліву орієнтацію. Впорядкована
трійка векторів
то їх можна поділити на такі, що мають
праву і ліву орієнтацію. Впорядкована
трійка векторів називаєтьсяправою,
якщо з кінця вектора
називаєтьсяправою,
якщо з кінця вектора
 найкоротший поворот від вектора
найкоротший поворот від вектора до вектора
до вектора спостерігається проти годинникової
стрілки (Рис. 18.1)
спостерігається проти годинникової
стрілки (Рис. 18.1)
|
|
|
Рис 18.1 |
У
протилежному випадку трійка векторів
 називаєтьсялівою.
називаєтьсялівою.
Векторним
добутком
вектора
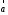 на вектор
на вектор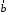 називається вектор
називається вектор що задовольняє наступним трьом умовам:
що задовольняє наступним трьом умовам:

 -
найменший кут між векторами
-
найменший кут між векторами
 і
і
 перпендикулярний
до кожного з векторів
перпендикулярний
до кожного з векторів
 і
і
трійка векторів
 має бути правою.
має бути правою.
Векторний
добуток позначається так:
 .
.
Як
можна бачити з визначення, модуль
векторного добутку за значенням дорівнює
площі паралелограма, побудованого на
векторах
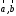 (Рис. 18.2)
(Рис. 18.2)
|
|
|
Рис 18.2 |
Основні властивості векторного добутку:
Операція векторного добутку не є комутативною. При зміні множників місцями напрямок векторного добутку змінюється на протилежний.
Дійсно,
розглянемо вектори
 і
і За
визначенням
За
визначенням
 але щоб трійки
але щоб трійки і
і
 були правими (Рис. 18.2), вектори
були правими (Рис. 18.2), вектори і
і мають мати протилежний напрямок, тому
мають мати протилежний напрямок, тому або
або
 841884\* MERGEFORMAT (.)
841884\* MERGEFORMAT (.)
Для будь-яких трьох векторів
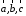
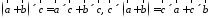 .
.
Для будь якої сталої

 .
.
Необхідна і достатня умова колінеарності.
Для
того, щоб два ненульових вектори
 і
і були колінеарні, необхідно і достатньо,
щоб їх векторний добуток дорівнював
нульовому вектору:
були колінеарні, необхідно і достатньо,
щоб їх векторний добуток дорівнював
нульовому вектору:
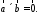 851885\* MERGEFORMAT (.)
851885\* MERGEFORMAT (.)
Нехай
 і
і - колінеарні і
- колінеарні і Тоді
Тоді - найменший кут, утворений цими векторами,
дорівнює
- найменший кут, утворений цими векторами,
дорівнює або
або В обох випадках
В обох випадках і
і отже,
отже,
Якщо виконується рівність 1885, тоді

Оскільки
 і
і то це можливо тільки тоді, коли
то це можливо тільки тоді, коли Але це означає, що
Але це означає, що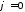 або
або тобто вектори розміщені на одній або
паралельних прямих.
тобто вектори розміщені на одній або
паралельних прямих.
Наслідком з доведеної теореми зокрема є таке: векторний добуток вектора на самого себе дорівнює нульовому вектору
 861886\* MERGEFORMAT (.)
861886\* MERGEFORMAT (.)
Векторні добутки базисних векторів системи координат.
Для
базисних векторів
 будь-якої прямокутної системи координат
будь-якої прямокутної системи координат виконуються рівності:
виконуються рівності:
 871887\* MERGEFORMAT (.)
871887\* MERGEFORMAT (.)
Можна бачити, що множення базисних векторів відбувається згідно з правилом кругової перестановки (Рис. 18.3)
|
|
|
Рис 18.3 |
Перші
три рівності у 1887 є безпосереднім
наслідком 1886. Доведемо, наприклад, що
 Дійсно, трійка векторів
Дійсно, трійка векторів є правою,
є правою, Також
Також Отже, дійсно
Отже, дійсно
Векторний добуток векторів заданих координатами.
Якщо
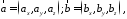 то
то
 881888\* MERGEFORMAT (.)
881888\* MERGEFORMAT (.)
Дійсно:

З урахуванням 1887 знаходимо

Кожний вираз в дужках є визначником другого порядку і тому результат може бути записаний у наступному вигляді:

Застосування векторного добутку.
Перевірка колінеарності двох векторів.
Як вже було доведено, необхідною і достатньою умовою колінеарності двох векторів є рівність 1885. За допомогою 1888 цю рівність можна записати у координатній формі:

Якщо усі координати векторів не дорівнюють нулю, з останніх рівностей знаходимо
 891889\* MERGEFORMAT (.)
891889\* MERGEFORMAT (.)
Рівність 1889 означає, що умовою колінеарності векторів є пропорційність їх відповідних координат.
Обчислення площі
 за відомими координатами його вершин:
за відомими координатами його вершин:

Розглянемо вектори:
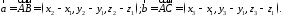
Площа
 дорівнює половині площі паралелограма,
побудованого на цих векторах:
дорівнює половині площі паралелограма,
побудованого на цих векторах:
 901890\* MERGEFORMAT (.)
901890\* MERGEFORMAT (.)
Знаходимо

де, згідно з 1888,

Тоді

Визначення моменту сили.
Якщо
точка
 твердого тіла зафіксована, а до точки
твердого тіла зафіксована, а до точки цього тіла прикладена сила
цього тіла прикладена сила то обертальний момент сили
то обертальний момент сили відносно точки
відносно точки дорівнює векторному добутку:
дорівнює векторному добутку:
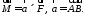 911891\* MERGEFORMAT (.)
911891\* MERGEFORMAT (.)
9219Equation Section (Next)§19. Мішаний (векторно-скалярний) добуток трьох векторів
Нехай
 - впорядкована трійка векторів. Якщо
векторний добуток перших двох векторів
- впорядкована трійка векторів. Якщо
векторний добуток перших двох векторів та
та скалярно помножити на третій вектор
скалярно помножити на третій вектор то отримане число
то отримане число називаєтьсямішаним
(векторно-скалярним) добутком трьох
векторів.
називаєтьсямішаним
(векторно-скалярним) добутком трьох
векторів.
Для цієї дії над векторами встановлюються такі властивості.
Мішаний добуток трьох некомпланарних векторів
 за абсолютною величиною дорівнює об’єму
паралелепіпеда, побудованого на цих
векторах, як на ребрах.
за абсолютною величиною дорівнює об’єму
паралелепіпеда, побудованого на цих
векторах, як на ребрах.
Розмістимо
вектори
 так, щоб вони виходили з однієї точки і
побудуємо на них паралелепіпед (Рис.
19.1).
так, щоб вони виходили з однієї точки і
побудуємо на них паралелепіпед (Рис.
19.1).
|
|
|
Рис 19.1 |
Об’єм побудованого паралелепіпеда дорівнює
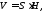
де
 - площа основи, а
- площа основи, а - його висота.
- його висота.
Нехай
 , тоді площа основи дорівнює
, тоді площа основи дорівнює

 - кут,
утворений векторами
- кут,
утворений векторами
 та
та Згідно з визначенням мішаного добутку
Згідно з визначенням мішаного добутку

де
 - кут, утворений векторами
- кут, утворений векторами і
і
У
випадку, коли трійка
 - права (див. Рис. 20.1),
- права (див. Рис. 20.1), і
і ,
, -
висота паралелепіпеда. У випадку лівої
трійки
-
висота паралелепіпеда. У випадку лівої
трійки і
і
Тому

Знак
 відповідає випадку правої, а
відповідає випадку правої, а лівої трійки векторів. отже, якщо взяти
мішаний добуток за абсолютною величиною,
то
лівої трійки векторів. отже, якщо взяти
мішаний добуток за абсолютною величиною,
то
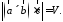 931993\* MERGEFORMAT (.)
931993\* MERGEFORMAT (.)
Якщо взяти трикутну призму або трикутну піраміду, побудовану на цих векторах (рис. 19.2), то
|
|
|
Рис 19.2 |

Мішаний добуток додатній, якщо
 - права трійка, і від’ємний у випадку
лівої трійки.
- права трійка, і від’ємний у випадку
лівої трійки.При перестановці місцями множників так, що не змінюється орієнтація трійки векторів, не змінюється значення мішаного добутку:

Якщо вектори задані координатами

 то
то
 941994\* MERGEFORMAT (.)
941994\* MERGEFORMAT (.)
Дійсно, згідно формули для векторного добутку 1888 і формули 1778, знаходимо скалярний добуток:

Необхідна і достатня умова компланарності. Для того, щоб три ненульові вектори були компланарними, необхідно і достатньо, щоб їх мішаний добуток дорівнював нулю:
 951995\* MERGEFORMAT (.)
951995\* MERGEFORMAT (.)
Доведення
необхідності.
Нехай
 - компланарні і розміщені у одній площині
- компланарні і розміщені у одній площині
 (Рис. 19.3):
(Рис. 19.3):
|
|
|
Рис 19.3 |
Вектор
 перпендикулярний до вектора
перпендикулярний до вектора
 і до вектора
і до вектора тому
тому а значить
а значить тому
тому
Доведення
достатності.
Нехай мішаний добуток дорівнює нулю:
 По-перше, це можливо, коли
По-перше, це можливо, коли .
Це означає, що
.
Це означає, що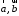 - колінеарні. Тому
- колінеарні. Тому можуть бути розміщені у одній площині.
можуть бути розміщені у одній площині.
Якщо
 то
то
 Але також
Але також і
і
 ,
отже, усі три вектори можуть бути
розміщені в площині
,
отже, усі три вектори можуть бути
розміщені в площині
 перпендикулярно до вектора
перпендикулярно до вектора
9620Equation Section (Next)§ 20. Задачі на застосування скалярного, векторного та мішаного добутків
Задача
20.1.
Дано вектори
 та
та .
Обчислити:
.
Обчислити:
1) ;
;
2)
 .
.
Розв’язання.
Знайдемо координати векторів співмножників.


Скалярний добуток знаходиться за формулою 1778:
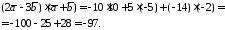
2)
Знайдемо координати
 .
.
Тоді
 .
.
Задача
20.2.
Дано вершини чотирикутника

 .
Довести, що його діагоналі перпендикулярні.
.
Довести, що його діагоналі перпендикулярні.
Розв’язання.
На
діагоналях чотирикутника розташовані
вектори
 та
та .
Перевіримо умову перпендикулярності
двох векторів 1776:
.
Перевіримо умову перпендикулярності
двох векторів 1776:
 ,
,
з чого й випливає перпендикулярність діагоналей чотирикутника.
Задача
20.3. Дано
вершини трикутника АВС:

 та
та
 .
Визначити його внутрішній кут при
вершиніВ.
.
Визначити його внутрішній кут при
вершиніВ.
Розв’язання.
Кут
при вершині
 –
це кут між векторами
–
це кут між векторами та
та .
Маємо
.
Маємо ,
, .
.
У нашому випадку, згідно 1780,
 .
.
 ,
,
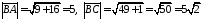 .
.
Тоді
 ,
отже, кут при вершиніВ
дорівнює
,
отже, кут при вершиніВ
дорівнює
 .
.
Задача
20.4.
Дано
вектори
 та
та ,
де
,
де ,
, ,
кут між векторами
,
кут між векторами та
та дорівнює
дорівнює .
Знайти:
.
Знайти:
1)
 ;
;
2) косинус
кута між векторами
 та
та .
.
Розв’язання.
Особливість
цієї задачі полягає в тому, що координати
векторів
 і
і
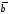 невідомі, тому не вдасться скористатись
зручною формулою для обчислення
скалярного добутку через координати.
Для обчислення скалярного добутку в
цій задачі ми будемо користуватись
властивостями скалярного добутку та
формулою 1775.
невідомі, тому не вдасться скористатись
зручною формулою для обчислення
скалярного добутку через координати.
Для обчислення скалярного добутку в
цій задачі ми будемо користуватись
властивостями скалярного добутку та
формулою 1775.
Обчислимо

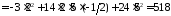 .
.
При обчисленні скористались тим, що
 .
.
Нехай
 ,
, .
Тоді
.
Тоді
 ,
,



В результаті маємо:
 .
.
Задача
20.5. Обчислити
роботу сили
 при переміщенні матеріальної точки з
положення
при переміщенні матеріальної точки з
положення в положення
в положення .
.
Розв’язання.
Переміщення
 .
Згідно 1781,
.
Згідно 1781,
 .
.
Задача
20.6. Обчислити
проекцію вектора
 на вектор
на вектор .
.
Розв’язання.
За формулою 1782
 .
.
Задача
20.7.
Дано
 та
та .
Знайти векторний добуток
.
Знайти векторний добуток .
.
Розв’язання.
Спочатку знайдемо координати вектора
 .
.
Далі
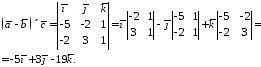
Задача
20.8.
Знайти площу паралелограма, побудованого
на векторах
 та
та .
.
Розв’язання.
Площа
паралелограма, побудованого на векторах
 і
і ,
знаходиться за формулою
,
знаходиться за формулою
 .
.
Обчислимо
векторний добуток
 :
:

Відповідно
 .
.
Задача
20.9. Знайти
площу паралелограма, побудованого на
векторах
 та
та ,
якщо відомо, що
,
якщо відомо, що ,
та кут між векторами
,
та кут між векторами і
і дорівнює
дорівнює .
.
Розв’язання.
Як і в
задачі 20.4,
особливість цієї задачі полягає в тому,
що координати векторів
 і
і
 невідомі. Для обчислення векторного
добутку в цій задачі скористаємось
властивостями векторного добутку та
формулою для знаходження модуля
векторного добутку:
невідомі. Для обчислення векторного
добутку в цій задачі скористаємось
властивостями векторного добутку та
формулою для знаходження модуля
векторного добутку:
 .
.
Використовуючи
властивості 1884, 1886векторного добутку,
виразимо векторний добуток
 через векторний добуток векторів
через векторний добуток векторів і
і :
:

Далі обчислимо площу паралелограма:
 .
.
Задача
20.10. Перевірити,
що чотири точки

 є вершинами трапеції.
є вершинами трапеції.
Розв’язання.
Знайдемо
координати векторів, які розташовані
на сторонах чотирикутника
 :
: ,
,
 ,
,
 ,
,
 .
.
У
нашому випадку, згідно 1889
 ,
так як
,
так як .
Значить дві сторони чотирикутника
паралельні. Покажимо, що інші дві сторони
не є паралельними:
.
Значить дві сторони чотирикутника
паралельні. Покажимо, що інші дві сторони
не є паралельними: .
.
Отже,
чотирикутник
 -
трапеція.
-
трапеція.
Задача
20.11. Дано
вершини трикутника
 .
Обчислити довжину висоти
.
Обчислити довжину висоти ,
проведеної з вершини
,
проведеної з вершини .
.
Розв’язання.
З одного боку, площу трикутника можна обчислити застосувавши векторний добуток:
 ,
,
а з другого-
 .
.
Прирівнявши праві частини наведених формул, легко знайдемо:
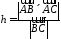 .
.
Обчислимо координати шуканих векторів та компоненти векторного добутку:
 ,
,
 ,
,
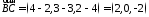 ,
,

Отже,

Задача
20.12. Сила
 прикладена
у точці
прикладена
у точці
 .
Знайти величину моменту сили відносно
точки
.
Знайти величину моменту сили відносно
точки .
.
Розв’язання.
Обчислимо
вектор
 .
За формулою 1891
.
За формулою 1891

 .
.
Тепер обчислимо величину моменту сили:
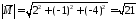 .
.
Задача
20.13. Дано
 та
та .
Знайти мішаний добуток
.
Знайти мішаний добуток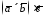 .
.
Розв’язання.
Мішаний добуток векторів можна знайти за формулою 1994:

Задача
20.14.
Знайти координату
 точки
точки ,
при якій чотири точки
,
при якій чотири точки ,
,
 лежать в одній площині.
лежать в одній площині.
Розв’язання.
Знайдемо
координати трьох векторів
 ,
, ,
, .
Далі помітимо, що задані чотири точки
розташовані в одній площині тоді, коли
три знайдені вектори компланарні. Для
цього необхідно, щоб їх мішаний добуток
був рівний нулю 1995:
.
Далі помітимо, що задані чотири точки
розташовані в одній площині тоді, коли
три знайдені вектори компланарні. Для
цього необхідно, щоб їх мішаний добуток
був рівний нулю 1995:

Для обчислення визначника скористаємось його розкладанням за елементами другого рядка.

Остання
рівність виконується при
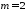 .
Отже, чотири точки знаходяться у одній
площині при
.
Отже, чотири точки знаходяться у одній
площині при .
.
Задача
20.15.
Знайти об’єм паралелепіпеда, побудованого
на векторах
 та
та ,
що виходять з однієї точки.
,
що виходять з однієї точки.
Розв’язання.
Об’єм
паралелепіпеда, побудованого на трьох
векторах
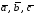 ,
що виходять з однієї точки, дорівнює
модулю мішаного добутку цих векторів
1993. Обчислимо мішаний добуток:
,
що виходять з однієї точки, дорівнює
модулю мішаного добутку цих векторів
1993. Обчислимо мішаний добуток:

Тоді об’єм паралелепіпеда
 .
.
Задача
20.16. Вершини
піраміди знаходяться в точках
 ,
, ,
, та
та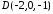 .
Обчислити:
.
Обчислити:
1)
площу грані
 ;
;
2)
площу перерізу, який проходить через
середину ребер
 ,
, ,
, ;
;
3)
об’єм піраміди
 .
.
Розв’язання.
1)
Грань піраміди представляє собою
трикутник. Обчислимо площу трикутника
 1890.
1890.
Маємо:
 ,
, .
Значить
.
Значить
 .
.
Остаточно
одержимо:
 .
.
Використовуючи формулу для знаходження координат середини відрізка, знаходимо середини
 ,
,
 ,
,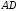 –
точки
–
точки
 ,
, ,
, відповідно. Площу перерізу знайдемо
за формулою
відповідно. Площу перерізу знайдемо
за формулою
 .
.
Координати
векторів
 ,
, ,
тоді
,
тоді
 ,
,
 .
.
3) Оскільки
 ,
,
знайдемо
координати векторів
 ,
, ,
, та
їх мішаний добуток:
та
їх мішаний добуток:
 .
.
Отже,
 .
.







