Задачі для самостійної роботи

1. Дано точки Обчислити.

2. Дано та. Знайти векторний добуток.

3. Обчислити площу паралелограма, побудованого на векторах , якщо.

4. Вектори іутворюють куті. Обчислити:.

5. Дано та. Знайти мішаний добуток цих векторів.

6. Дано вершини чотирикутника . Перпендикулярні чи ні його діагоналі?

7. Вектори іперпендикулярні і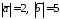. Обчислити.

8. Довести, що чотирикутник з вершинами квадрат і обчислити його площу.

9. Обчислити об’єм піраміди :

10. При якому значенні m вектори перпендикулярні?

11. Довести, що точки лежать у одній площині

12. Знайти вектор, який перпендикулярний до векторів та

13. Знайти скалярний добуток векторів та, де

14. Обчислити площу трикутника , якщо

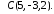
15. Перевірити, чи компланарні вектори , ,.

16. Обчислити кут при вершині трикутника, якщо

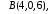
17. Сила прикладена у точці . Обчислити значення моменту цієї сили відносно точки та його напрямні косинуси.

18. При якому чотири точки, 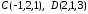лежать в одній площині?

19. Вершини піраміди знаходяться в точках , ,та.Обчислити: 1) площу грані ;2) об’єм піраміди .

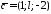20. При якому вектори, , утворюють ліву трійку?

21. Дано вершини піраміди: ,.Знайти висоту, проведену з вершини .

22. Дано точки і. Знайти проекцію векторана вектор.

Питання для повторення

1. Скалярний добуток, його властивості та застосування.

2. Векторний добуток, його властивості та застосування.

3. Змішаний добуток, його властивості та застосування.

9721Equation Section (Next)§ 21. Розкладення вектора по некомпланарним векторам. Базис тривимірного простору. Базис на координатній площині

Теорема. Якщо вектори некомпланарні, то кожний векторподається комбінацією цих векторів однозначно:

982198\* MERGEFORMAT (.)

Покажемо, що завжди існують числа такі, що виконується рівність 2198. Якщо цю рівність записати у координатному вигляді, то отримаємо систему лінійних алгебраїчних рівнянь

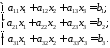992199\* MERGEFORMAT (.)

_{Оскільки вектори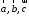} не компланарні, то визначник цієї системи відмінний від

10021100\* MERGEFORMAT (.)

Тому система 21100 завжди має єдиний розв’язок.

Будь-які три некомпланарні вектори називаютьсябазисом тривимірного простору. Рівність 2198 називається розкладенням вектора у цьому базисі, а числа‑ його координатами у базисі

Якщо вектори ‑ мають одиничні довжини і взаємно перпендикулярні, то утворений ними базис називаєтьсяортонормованим. Для цих векторів виконуються рівності:

10121101\* MERGEFORMAT (.)

Якщо порівняти рівності 21101 і 1777, то можна бачити, що базисні вектори будь-якої системи координатутворюють ортонормований базис тривимірного простору.

Аналогічно встановлюється, що два довільних некомпланарних вектори утворюють базис на координатній площині. Будь-який інший вектор з цієї площини може бути розкладений в цьому базисі:

Числа називаються координатами векторав базисі. Базисні векторидвомірної системи координатутворюють на площині ортонормований базис.

10222Equation Section (Next)§22. Матриця переходу від одного базису до іншого. Перетворення координат. Формули паралельного перенесення і повороту

Розглянемо у просторі два ортонормованих базиси 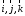і, а також пов’язані з ними системи координаті(Рис.22.1):

Рис 22.1

_{Кожен з векторів} може бути розкладеним по векторам

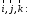
10322103\* MERGEFORMAT (.)

З координат цих векторів у базисі можна скласти матрицю:

10422104\* MERGEFORMAT (.)

Матриця називаєтьсяматрицею переходу від базису до базису. За допомогою цієї матриці формули 22103 можна переписати у вигляді:

10522105\* MERGEFORMAT (.)

Елементами матриці переходу є косинуси кутів, що утворюють вектори з осями системи координат. Дійсно,

10622106\* MERGEFORMAT (.)

В цих формулах‑ кути між векторамиі координатними осями.

Оскільки вектори утворюють ортонормований базис, то з 21101 випливають рівності:

10722107\* MERGEFORMAT (.)

За допомогою 22107 можна безпосередньо перевірити, що

,

де 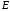‑ одинична матриця.

Остання рівність означає, що для матриці переходу завжди існує обернена, яка дорівнює транспонованій матриці переходу:

Тому з 22105 знаходимо

10822108\* MERGEFORMAT (.)

Формули 22105-22108 значно спрощуються у випадку координатної площини (Рис.22.2).

Рис 22.2

Нехай ‑ кут між векторомі віссю. Тоді з 22106 знаходимо

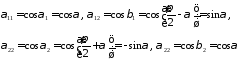
Отже, матриця переходу дорівнюватиме

Зв'язок між двома базисами здійснюється за формулами:

Матриця переходу необхідна для встановлення зв’язку між координатами точки у різних системах координат. Нехай точка у системімає координати, а у системі‑ координати. Відносно точкиприпустимо, що її координати у системіє числа. Розглянемо вектори

Як можна бачити (Рис.23.1), , тому

.

Скористаємось формулою 22105:

З останньої рівності випливає:

Внаслідок транспонування обох частин і врахування 22106 остаточно знаходимо:

10922109\* MERGEFORMAT (.)

Покоординатний запис 22109 має вигляд:

11022110\* MERGEFORMAT (.)

Якщо 22109 переписати у вигляді

і помножити обидві частини на матрицю переходу , враховуючи щото отримаємо наступні формули:

11122111\* MERGEFORMAT (.)

Формули 22110, 22111 називаються формулами перетворення координат.

Розглянемо важливі частинні випадки цих формул. Нехай вісі систем координат івзаємно паралельні і однаково спрямовані, тобто системаотримана зпаралельним перенесенням у точку. У цьому випадку матриця переходу‑ одинична. Тому формули 22110, 22111 набувають вигляд

11222112\* MERGEFORMAT (.)

Формули 22112 називаються формулами паралельного перенесення систем координат.

Далі розглянемо системи координат 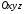і, початкові точки яких збігаються. У цьому випадкуможе бути отримана зшляхом повороту і. Тоді формули 22110 і 22111 перетворюються наступним чином

11322113\* MERGEFORMAT (.)

Ці формули називаються формулами повороту системи координат.

При переході до координатної площини, з 22112 і 22113 маємо:

11422114\* MERGEFORMAT (.)

11522115\* MERGEFORMAT (.)

Формули 22115 пропонується вивести самостійно.

11623Equation Section (Next)