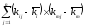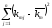- •Тема 1 Риск как экономическая категория
- •1. Понятие риска, его основные элементы
- •2. Причины возникновения неопределенности и риска
- •3. Общие принципы классификации рисков
- •4.Факторы, влияющие на уровень экономического риска
- •Тема 2: Организация процесса управления риском
- •2. Общая схема процесса управления риском
- •Тема 3 Методы выявления и анализа риска
- •Тема 4. Оценка степени риска
- •Частный пример карты рисков
- •Тема 5 Методы управления риском
- •1. Классификация методов управления рисками
- •2. Прогнозирование внешней экономической обстановки.
- •5. Создание системы резервов.
- •6. Привлечение внешних ресурсов.
- •2. Методы уклонения от риска
- •Тема 6. Сущность, содержание и виды страхования.
- •2. Перестрахование
- •Тема 7: Оценка эффективности методов управления риском
- •Тема 8 Управление финансовыми рисками
- •1. Сущность и классификация финансовых рисков
- •2. Политика управления финансовыми рисками
- •3. Внутренние механизмы управления финансовыми рисками
- •Тема 9. Инвестиционный менеджмент и риск
- •Ситуация усложняется при переходе к портфелям с большим числом входящих в них активов. В этом случае возникает ряд проблем как теоретического, так и вычислительного характера.
- •3. Принципы формирования портфеля инвестиций
- •Модель оценки доходности финансовых активов
- •Доходность
- •5. Анализ инвестиционных проектов в условиях риска Имитационная модель оценки риска
- •Методика изменения денежного потока
Доходность

M
km
krf
1 Риск
ценной бумаги
(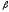 )
)
Рис. 6.1. Логика представления модели САРМ
Исходя из приведенных выше предпосылок, доказывается, что искомая зависимость у = f(x) представляет собой прямую линию.
Итак, мы имеем две точки с координатами (0, krf) и (1, km). Из курса геометрии известно, что уравнение прямой, проходящей через точки (х1, y1) и (х2, у2) задается формулой:
|
х – х1 |
= |
y – y1 |
|
x1 –x2 |
y1 – y2 |
(10.6)
Подставляя в формулу исходные данные, получим:
y = krf + (km— krf) x (10.7)
Имея
в виду, что переменная х представляет
собой риск, характеризуемый показателем
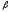 ,
а у—
ожидаемую
доходность ke,
получим следующую формулу, которая и
является моделью САРМ:
,
а у—
ожидаемую
доходность ke,
получим следующую формулу, которая и
является моделью САРМ:
y
= krf
+
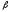 (km
-
krf)
(10.8)
(km
-
krf)
(10.8)
где ke — ожидаемая доходность акций данной компании;
krf — доходность безрисковых ценных бумаг (в частности, в США берут за основу государственные казначейские векселя, используемые для краткосрочного (до 1 года) регулирования денежного рынка);
km — ожидаемая доходность в среднем на рынке ценных бумаг;
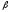 —
бета-коэффициент
данной компании.
—
бета-коэффициент
данной компании.
Показатель (km — krf) имеет вполне наглядную интерпретацию, представляя собой рыночную (т.е. в среднем) премию за риск вложения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации корпораций и пр.). Аналогично, показатель (ke—krf) представляет собой премию за риск вложения капитала в ценные бумаги именно данной компании. Модель САРМ означает, что премия за риск вложения в ценные бумаги данной компании прямо пропорциональна рыночной премии за риск.
Систематический
риск в рамках модели САРМ измеряется с
помощью
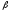 -коэффициентов
(бета-коэффициентов). Каждый вид ценной
бумаги имеет собственный
-коэффициентов
(бета-коэффициентов). Каждый вид ценной
бумаги имеет собственный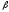 -коэффициент,
представляющий собой индекс доходности
данного актива по отношению к доходности
в среднем на рынке ценных бумаг. Значение
показателя
-коэффициент,
представляющий собой индекс доходности
данного актива по отношению к доходности
в среднем на рынке ценных бумаг. Значение
показателя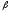 рассчитывается по статистическим данным
для каждой компании, котирующей свои
ценные бумаги на бирже, и периодически
публикуется в специальных справочниках.
рассчитывается по статистическим данным
для каждой компании, котирующей свои
ценные бумаги на бирже, и периодически
публикуется в специальных справочниках.
Например,
имеется совокупность показателей
доходности по группе компаний за ряд
периодов {kij},
где kij
| —
показатель
доходности 1-й
компании
(i
= l,
2,...,
t)
в j-м
периоде (j
=
1, 2,..., n).
Тогда
общая формула расчета
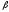 -коэффициента для произвольнойі-ой
компании
имеет вид:
-коэффициента для произвольнойі-ой
компании
имеет вид:
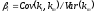
(10.9)
где
|
Cov(ki,km) |
= |
1 |
|
|
n |
|
Var(km) |
= |
1 |
|
|
n |
В целом
по рынку ценных бумаг
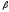 -коэффициент равен единице; для
отдельных компаний он колеблется около
единицы, причем большинство
-коэффициент равен единице; для
отдельных компаний он колеблется около
единицы, причем большинство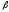 -коэффициентов находится в интервале
от0,5
до
2,0.
Интерпретация
-коэффициентов находится в интервале
от0,5
до
2,0.
Интерпретация
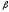 -коэффициента для акций конкретной
компании заключается в следующем:
-коэффициента для акций конкретной
компании заключается в следующем:
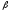 =
1
означает,
что акции данной компании имеют среднюю
степень риска, сложившуюся на рынке в
целом;
=
1
означает,
что акции данной компании имеют среднюю
степень риска, сложившуюся на рынке в
целом;
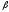 <
1
— что
ценные бумаги данной компании менее
рискованны, чем в среднем на рынке
(так,
<
1
— что
ценные бумаги данной компании менее
рискованны, чем в среднем на рынке
(так,
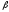 =
0,5 означает,
что данная ценная бумага в два раза
менее рискованна, чем в среднем по
рынку);
=
0,5 означает,
что данная ценная бумага в два раза
менее рискованна, чем в среднем по
рынку);
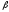 >
1
— что
ценные бумаги данной компании более
рискованны, чем в среднем на рынке;
>
1
— что
ценные бумаги данной компании более
рискованны, чем в среднем на рынке;
увеличение
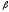 -коэффициента в динамике
свидетельствует о том, что вложения в
ценные бумаги данной компании становятся
более рискованными;
-коэффициента в динамике
свидетельствует о том, что вложения в
ценные бумаги данной компании становятся
более рискованными;
снижение
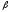 -коэффициента в динамике
—
о
том, что вложения в ценные бумаги данной
компании становятся менее рискованными.
-коэффициента в динамике
—
о
том, что вложения в ценные бумаги данной
компании становятся менее рискованными.
Как отмечено выше, модель САРМ разработана исходя из ряда предпосылок, часть из которых не выполняется на практике, например, налоги и трансакционные затраты существуют, инвесторы находятся в неравных условиях, в том числе и в отношении доступности информации и т.п. Поэтому модель не является идеальной и неоднократно подвергалась как критике, так и эмпирической проверке. Особенно интенсивно исследования в этом направлении велись с конца 60-х годов, а их результаты нашли отражение в сотнях статей. Существуют различные точки зрения по поводу модели, поэтому приведем некоторые наиболее типовые представления о современном состоянии этой теории из обзора, сделанного Ю. Бригхемом и Л. Гапенски.
1. Концепция САРМ, в основе которой лежит приоритет рыночного риска перед общим, является весьма полезной, имеющей фундаментальное значение в концептуальном плане. Модель логично отражает поведение инвестора, стремящегося максимизировать, свой доход при заданном уровне риска и доступности данных.
2. Теоретически САРМ дает однозначное и хорошо интерпретируемое представление о взаимосвязи между риском и требуемой доходностью, однако она предполагает, что для построения связи должны использоваться априорные ожидаемые значения переменных, тогда как в распоряжении аналитика имеются лишь апостериорные фактические значения. Поэтому оценки доходности, проведенные с помощью модели, потенциально содержат ошибки.
3.
Некоторые
исследования, посвященные эмпирической
проверке модели, показали на
значительные отклонения между
фактическими и расчетными данными,
что позволило ученым подвергнуть
эту
теорию серьезной критике. В частности,
к ним
относятся
Ю. Фама и К. Френч, которые изучили
зависимость между
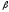 -коэффициентами
и доходностью нескольких тысяч акций
по данным за пятьдесят лет'. По мнению
Бригхема и Гапенски, модель САРМ описывает
взаимосвязи между ожидаемыми значениями
переменных, поэтому любые выводы,
основанные на эмпирической проверке
статистических данных, вряд ли правомочны
и не могут опровергнуть теорию.
-коэффициентами
и доходностью нескольких тысяч акций
по данным за пятьдесят лет'. По мнению
Бригхема и Гапенски, модель САРМ описывает
взаимосвязи между ожидаемыми значениями
переменных, поэтому любые выводы,
основанные на эмпирической проверке
статистических данных, вряд ли правомочны
и не могут опровергнуть теорию.
Тем не менее, многие ученые понимают — один из основных недостатков модели заключается в том, что она является однофакторной. Указывая на этот недостаток, известные специалисты Дж. Вестон и Т. Коуплэнд приводят такой образный пример. Представьте себе, что ваш маленький самолет не может совершить посадку из-за сильного тумана и на вопрос диспетчерам о помощи вы получаете информацию о том, что самолет находится в ста милях от посадочной полосы. Конечно, информация весьма полезна, но вряд ли достаточна для успешной посадки.
В научной литературе известны три основных подхода, альтернативных модели САРМ:
теория арбитражного ценообразования,
теория ценообразования опционов,
теория преференций состояний в условиях неопределенности.
Наибольшую известность получила теория арбитражного ценообразования (Arbitrage Pricing Theory — APT). Концепция APT была предложена известным специалистом в области финансов, профессором Йельского университета Стивеном Россом. В основу модели заложено естественное утверждение о том, что фактическая доходность любой акции складывается из двух частей: нормальной, или ожидаемой, доходности и рисковой, или неопределенной, доходности. Последний компонент определяется многими экономическими факторами, например, рыночной ситуацией в стране, оцениваемой валовым внутренним продуктом, стабильностью мировой экономики, инфляцией, динамикой процентных ставок и др. Таким образом, модель может и должна включать множество факторов.
Данная модель обладает как достоинствами, так и недостатками. Прежде всего она не предусматривает таких жестких исходных предпосылок, которые свойственны модели САРМ. Количество и состав релевантных факторов определяется аналитиком и заранее не регламентируется. Фактическая реализация модели связана с привлечением весьма сложного аппарата математической статистики, поэтому до настоящего времени теория АТР носит достаточно теоретизированный характер. Тем не менее, главное достоинство этой теории заключается в том, что доходность является функцией многих переменных, и потому эта теория рассматривается многими учеными как одна из наиболее перспективных.
Две другие альтернативы модели САРМ — теория ценообразования опционов (Option Pricing Theory — ОРТ) и теория преференций состояний в условиях неопределенности (State-Preference Theory — SPT) — по тем или иным причинам еще не получили достаточного развития и находятся в стадии становления. В частности, в отношении теории SPT можно упомянуть, что она носит весьма теоретизированный характер и, например, подразумевает необходимость получения достаточно точных оценок будущих состояний рынка. Зарождение теории ОРТ связывают с именами Ф. Блэка и М. Скоулза, а теории преференций — с именем Дж. Хиршлифера.