Поляризация волн

Полагаем, что вектор Е имеет две составляющие, и. Найдем положение кривой, которая служит геометрическим местом концов вектора Е суммарного процесса.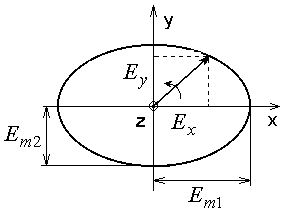

Перепишем:

,

возводим их в квадрат и складываем:

,

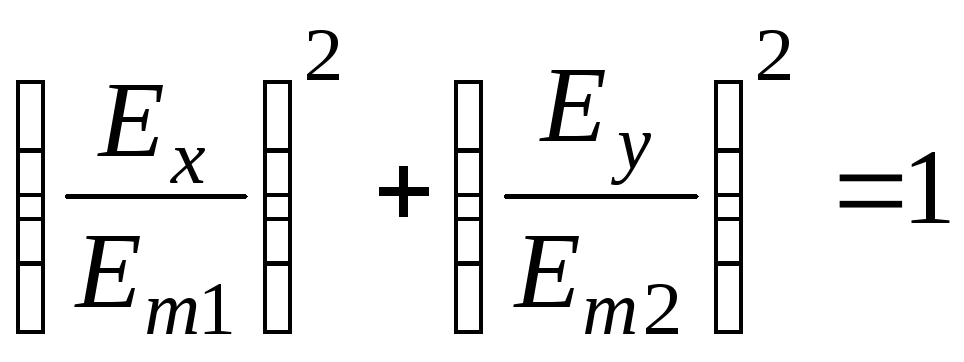это уравнение эллипса, а про волну говорят, что это эллиптически поляризованная волна.

В этом случае вектор Е вращается против часовой стрелки, если смотреть с конца i_z – лево поляризованная волна.

Частные случаи:

Равна нулю одна из составляющих или сдвиг фаз между ними равен нулю. Тогда конец вектора Е перемещается вдоль линии произвольно, в общем случае, ориентированной относительно системы координат. Волна – линейно поляризованная.

Равны амплитуды Е_m1 = Е_m2, а сдвиг фаз - 90. Тогда кривая окружность, волну называют волной с круговой поляризацией.

Легко заметить, что суперпозиция двух волн с линейными поляризациями, сдвинутых по фазе и пространственно на 90, дают эллиптически поляризованную волну, две волны с круговыми поляризациями и противоположными направлениями вращения в результате суперпозиции дают волну линейно поляризованную.

Граничные условия для векторов эмп

1. Нормальные составляющие

Соотношения, показывающие связь между значениями векторов ЭМП в разных средах, у поверхности раздела называют граничными условиями. (Используют интегральную запись уравнений Максвелла). На поверхности раздела двух сред с параметрами соответственно, выделим малый элемент так чтобы:

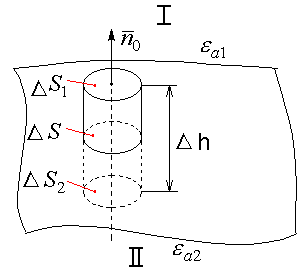
1. его можно считать плоским;

2. распределение Dn в пределах 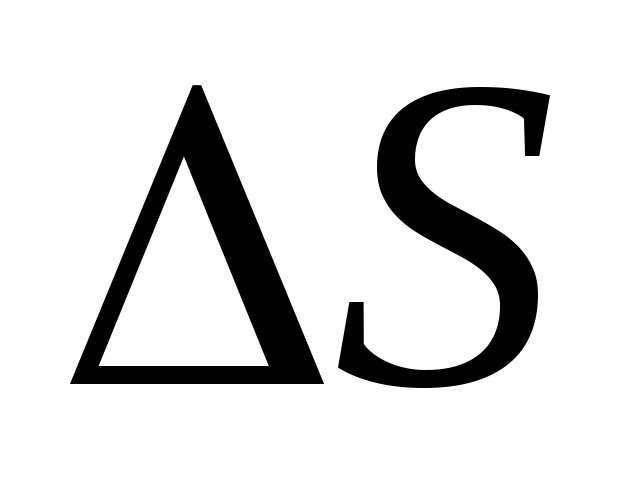должно быть равномерным.

Построим на цилиндр с основаниями в разных средах. Используем третье уравнение Максвелла:

.

Поверхность цилиндра:

.

Устремим так, чтобыоставались в разных средах:

;

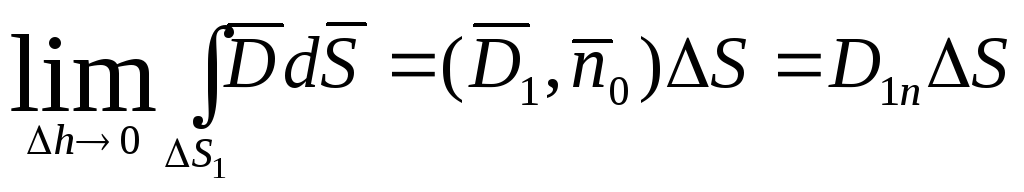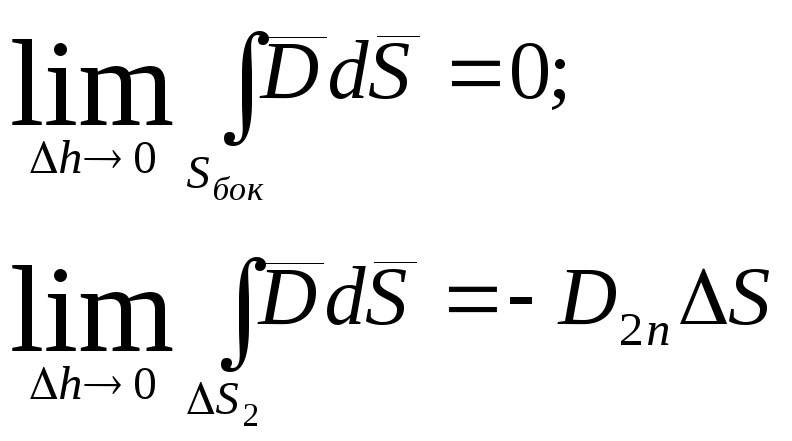
Если заряд не сосредоточен на поверхности раздела, то:

и нормальная компонента вектора непрерывна при переходе из одной среды в другую. Если заряд распределен по поверхности раздела в виде бесконечно тонкого слоя с поверхностной плотностью:

тогда , то есть нормальная компонента вектораD претерпевает скачек на величинуповерхностного заряда. Для вектора Е:

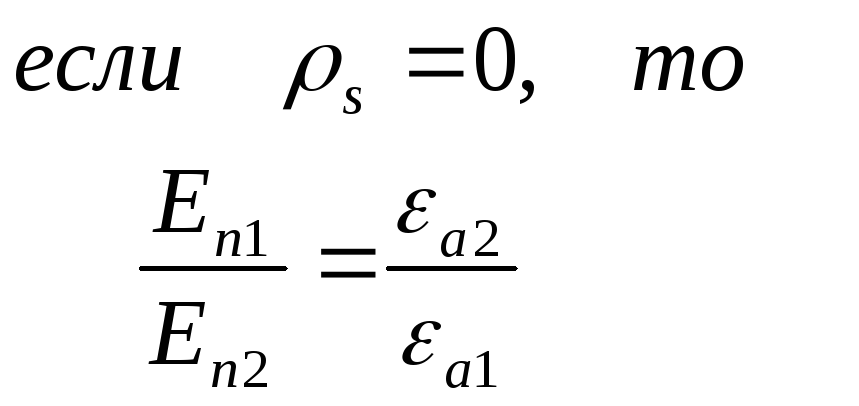
Нормальная компонента Е претерпевает разрыв. На самом деле поверхностных зарядов не бывает, толщина слоя конечна и D меняется постепенно. Но математическая модель удобнее.

Тангесальные составляющие

Из произвольной точки на поверхности S раздела двух изотропных сред проведем единичную нормаль n₀. Через нее проведем плоскость Р и на линии пересечения Р и S выделим малый отрезок  l такой, чтобы считать его прямолинейным и  неизменной в его пределах.

На отрезке l построим контур ABCD высотой h

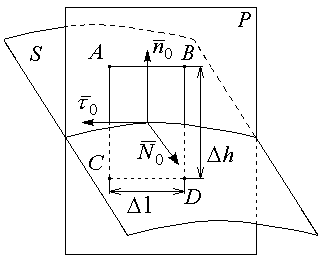
- касательная к  l,

- нормаль к P, образующий правовинтовую систему с ABCD и .

Используем второе уравнение Максвелла:

,

где

.

Левую часть представим в виде суммы четырех интегралов:

и оставляя AB и CD в разных средах, устремляем h  :

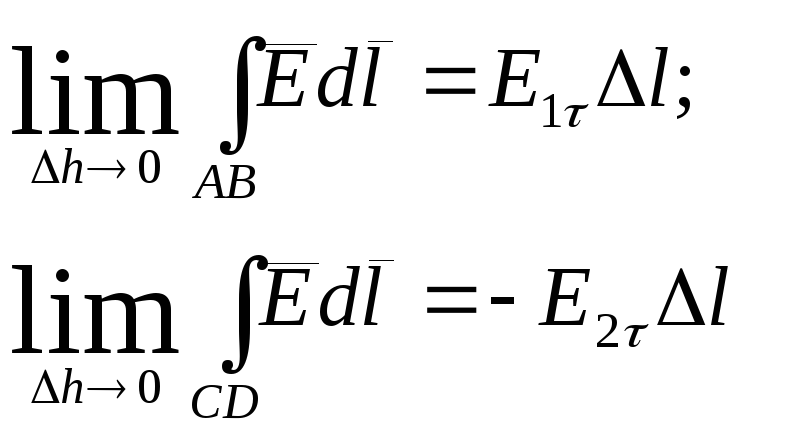
Так как Е и конечные величины, то:

.

А , то есть касательная, составляющая вектора Е, непрерывна при переходе через границу раздела двух сред.

Полная система граничных условий:

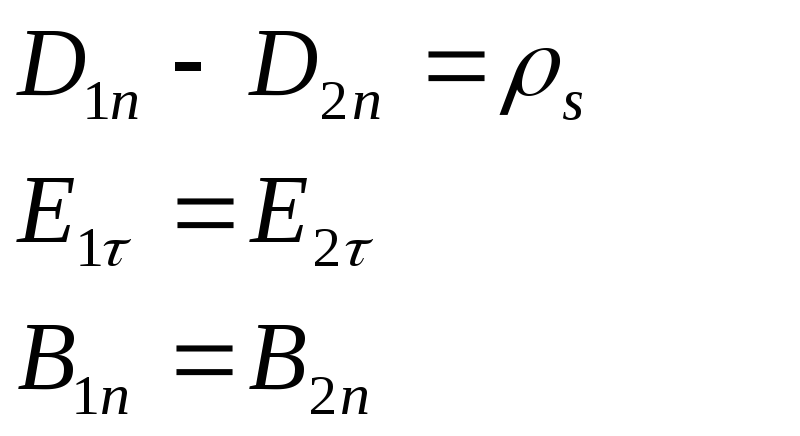
где - плотность поверхностного тока, направленного ортогонально вектору(или его составляющая).

На поверхности раздела с идеальным проводником , внутри которого поле отсутствует, согласно уравнению Максвелла будут справедливы следующие граничные условия:

,

или для Н в векторной форме: