1. Линейная регрессия

Исходные данные: У=а₀+а₁*Х

Без аномальных.

Выделить массив----> Построить точечную диаграмму (5 графиков) ---->Выделить диаграмму---->Меню «Диаграмма» ---->макет---->Линия тренда---->Дополнительные параметры линии тренда---->в Окне: Уравнение линии, ∆показывать уравнение на диаграмме, ∆поместить на диаграмму величину достоверности апроксимации (коэф. Детерминации R²)---->ОК

Получается диаграмма

2. Нелинейная парная регрессия.

А) полиномиальная регресия: у=а₀+а₁*х1+а₂*х2

Б) Экспоненциальная регрессия: у=а₀*е^а1*х

В) Логарифмическая зависимость: у=а₀+а₁*lnX

Г) Степенная зависимость: у= а₀*Х^а1

Выделить массив----> Построить точечную диаграмму (5 графиков) ---->Выделить диаграмму---->Меню «Диаграмма» ---->макет---->Линия тренда---->Дополнительные параметры линии тренда---->в Окне: Уравнение линии, ∆показывать уравнение на диаграмме, ∆поместить на диаграмму величину достоверности апроксимации (коэф. Детерминации R2)---->ОК

22. Множественная регрессия. Формулы. Расчеты на ЭВМ.

Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными (Х) и зависимой переменной (У). Находится зависимость У от входных факторов и оценить силу связи.

n-объем выборки

k – число факторов

У= f(x1….. Хk) – уравнение множественной регресии.

Характеризует среднее значение выходного показателя, при заданных значениях входных факторов.

Построение графика

У= f(x1) – парная регрессия

У= f(x1, x2) – двухфакторная множественная модель

Виды:

1. Линейная множественная регрессия

у=а0+а1*х1+а2*х2+ а3*х3+ а4*х4+………+ аk*хk

а0, а1, а2, а3,….. аk – параметры модели

х1, х2, х3, х4,….. хk – переменные модели

График – поверхность.

2. Нелинейная множественная регрессия

У= f(x1….. Хk)

График – криволинейная поверхность.

Расчет в Ексель:

Исходные данные: У= f(x1, x2, x3, x4)

у=а0+а1*х1+а2*х2+ а3*х3+ а4*х4

Меню данные----> «Анализ данных» ----> «Регрессия» ----> в окне: вх. Инт х, вх инт. У- с заголовком, метки, уравнение надежности, остатки---->лист---->ОК

23. Корреляционная матрица. Граф связей. Обоснования вида модели для экологического прогнозирования.

Корреляционная матрица - определяется многофакторной модели и состоит из коэфициента парной корреляции (r_x,y).

r_x,y=xy-x*y/σ_x*σ_{y –} хар-т силу связи между Х и У. [-1;1]

	У	Х1	Х2	Х3	Х4
У	1	r y,x1	r y,x2	r y,x3	r y,x4
Х1	rx1,y	1	rx,y	rx,y	rx,y
Х2	rx2,y	rx,y	1	rx,y	rx,y
Х3	rx3,y	rx,y	rx,y	1	rx,y
Х4	rx4,y	rx,y	rx,y	rx,y	1

В Ексель:

Меню данные----> «Анализ данных» ---->»Корреляция» ----> в окне: вх. Инт х, вх инт. У- с заголовком, столбцы, метки---->лист---->ОК

Граф связей – это множество вершин-объекты исследования и множество связей между вершинами (отношения между объектами).

G=(X, U)

X – множество вершин

U – множество связей (дуг, ребер)

Бывает взвешенный граф (Ориентированный) – граф с весами для каждого ребра.

G=(X, U, ƹ)

Ƹ – вес

Связь между Х не должна быть сильной (<0,8)

Нужно брать те факторы, у которых связь с У сильная.

При помощи метода исключения получаем 3 модели:

24. Показатели качества парной и множественной регрессии.

Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.

Для оценки качества модели регрессии используются специальные показатели.

Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:

1) парной линейный коэффициент корреляции, который рассчитывается по формуле:

где G(x) – среднеквадратическое отклонение независимой переменной;

G(y) – среднеквадратическое отклонение зависимой переменной.

Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии

по формуле:

Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.

2) коэффициент детерминации рассчитывается как вадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.

Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.

Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:

G2(y)=

где G2(y) – это общая дисперсия зависимой переменной;

– это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:

– необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:

С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:

1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:

Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.

2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:

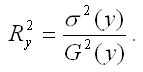
Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;

3) показатель

характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;

4) среднеквадратическая ошибка модели регрессии (Mean square error – MSE):

где h– это количество параметров, входящих в модель регрессии.

Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений то модель регрессии можно считать качественной.

Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:

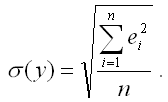
5) показатель средней ошибки аппроксимации рассчитывается по формуле:

Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.

25. Проверка регрессионной множественной модели на адекватность.

Используем критерий Фишера.

Выдвигаем гипотезы:

Н0: модель адекватна

Н1: модель неадекватна

Вычисляем наблюдаемое значение:

Fнабл=MSR/MSE, где

MSR=SSR/k – среднее (объясненная регрессия)

MSE=SSE/n-k-1 – случайная регрессия

Чем Fнабл > тем модель более адекватна.

Имеется критическое значение:

Fкрит=F(α; k; n-k-1) – Fкрит по таблице.

Сравниваем:

1. Fнабл > Fкрит. Принимаем Н0, т.е. модель адекватна.

2. Fнабл < Fкрит. Модель не адекватна. Принимаем Н1 ищем др модель. В табл. отражается Fкрит.

Если Р>0,1 то модель признаем не адекватной. Чем больше, тем лучше.

26. Средняя квадратическая ошибка уравнения, средняя относительная погрешность модели. Шкала оценки точности прогноза.

СКО уравнения (формула и что обозначает)

Обозначает среднее отклонение от линии регрессии

Средняя относительная погрешность

Означает точность модели. Чем

меньше, тем лучше.

Шкала оценки.

	<10%	10-20%	20-50%	>50%
Вывод	Отличная точность прогноза	Хорошая точность	Удовлетворительная точность	Неудовлетворительная точность

27. Основные термины временного ряда: временной ряд; случайный процесс; эквидистантные и не эквидистантные наблюдения; дискретное время, горизонт прогноза.

Временным рядом называется дискретная последовательность чисел, характеризующий состояние объекта наблюдения в отдельный момент времени.

n –кількість років (довжина реалізації)

мал.1 – Графічне зображення часового ряду

Временные ряды различают:

1. С одинаковым интервалом - Эквидистантные ряды

2. С разными интервалами – не Эквидистантные ряды

Длина ряда - количество точек временного ряда N.

Дискретное время - номер точки наблюдения.

Основные методы анализа временных рядов -

1. Графическая визуализация (визуальный экспресс-анализ)

2. Спектральный анализ

3. Автокорреляционный анализ

4. Вайлет анализ

5. Сглаживание

6. Метод сезонной декомпозиции

Горизонт прогноза – кол-во интервалов времени, на кот делается прогноз на данной модели (на сколько периодов делается прогноз).

28. Структура временного ряда: тренд, сезонная компонента, случайная компонента. Аддитивная и мультипликативная модели временного ряда.

Временной ряд может содержать:

Трендовую компоненту (линейную или нелинейную)Т

Сезонную компоненту (циклическую) S

Случайную компоненту Е

Общая модель имеет вид:

Х=Т+Е+S аддитивная

Х=Т*Е*S мультипликативная, и др.

28. Задачи временного ряда. Графическая визуализация ряда.

Основной задачей временного ряда является

определить структуру ряда

сделать прогноз

Метод графической визуализации

На основе исходных данных строится график временного ряда и делается предварительный вывод.

а0-средний уровень ряда

а-амплитуда колебаний

Т - период колебаний

Это гармоничная модель ряда

-циклическая частота

Частота

Различают

Высокочастотные и низкочастотные колебания

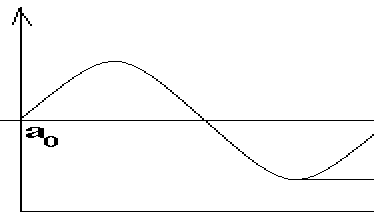
Циклический процесс-процесс периодизации

Квазоперіодичний процес

Стаціонарні процеси

Не стаціонарні, за математичним очікуванням

Нестаціонарні за дисперсією

Модель з сезонной компонентой и трендом

28. Спектральный анализ (назначение, расчетные формулы, основная частота, периодограмма, спектральная плотность, спектральный анализ в пакете «STATISTICA».

Это математическое разложение функции на сумму гармонических функций.

Для данных колебаний имеет место формула:

к=1, де

t_i= t₁, t₂, t₃, t₄, реальні

а_о –постійна величина

а_к, b_k –постійні коефіціенти (при cos та sin)

N –довжина ряду, завжди ціле число

к -1, 2, 3, ...

В дискретному часі

В результате получается:

Для каждой частоты возможно построить определенный график, сложить их и в результате получить исходный временной ряд.

Частоті більше, а період менше

В результаті отримується

Сложный эффект разлагается на простые и выполняется анализ простых, после чего делается вывод о сложном.

Спектральная плотность

Х_і -временной ряд

N-длина ряда

а_к, в_к-коэффициент разложение

Має місце формула:

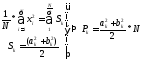
Расчет выполнялся в пакете «STATISTICA». Меню «Статистика»→ Дополнительные линейные/нелинейные модели→ Прогноз/серия времени → Выбор переменной Х → Spectral analyses→Advanced (убрать среднюю и убрать тренд)→Single series (одиночные ряды)→Quick→Summary (Итоги)→ Выбрать график Periodogram (Period)→OK.Результаты были отображены в таблицеSummary (Итоги) и на графике Period.

28. Автокорреляционный анализ временного ряда.

Имеем временной ряд

Существуют временные ряды в которых нынешнее существенно зависит от прошлого

Для выполнения проверки зависимости значений временного ряда между собой состоит ряд со сдвигом (Лагом):

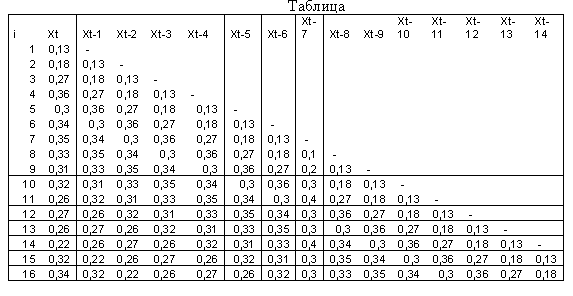
кількість зсувів

по данной таблице находят коэффициент корреляции между парами:

Для этого в Excel выбирается-статистические –КОРРЕЛ

28. Метод скользящей средней. Метод текущей средней.

Метод скользящей средней - используется на предыдущем этапе для извлечения случайности;

Идея метода - замена значений каждой точки ряда на некоторое среднее полученное по соседним точкам.

дискретное время

Сглаживание по 3-м точкам:

В результате получается график

 

Расчет в компьютере:

 Занести исходные данные

 с помощью сылок и формул заполнить таблицу и воспользоваться автозаполнением

 построить график.

Метод текущей средней - также служит для сглаживания и удаления случайных величин, но имеет другой принцип.

Идея метода: на каждом шагу среднее значение находится за всеми предыдущими включая фактическое.

 

В результате получается таблица и график

28. Метод экспоненциального сглаживания.

Метод экспоненциального сглаживания - используется для сглаживания, используются как реальные данные так и уже сгладжени.

Идея метода: для сглаживания используются как фактические данные так и сглаживания данных.

Ренкурентна формула:

 

где ,  безразмерные коэффициенты

 

Характеризуют степень доверия к фактическим данным и сглаженных

р-порядок средних

 

Чем больше порядок сглаживания тем модель точнее, но расчет тяжелее.

Частный случай:

Модель экспоненциального сглаживания 0-го порядка (р = 1)

 

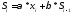
Предельные случаи:

а) =1; =0 – довіра лише фактичним даним

б) =0; =1 -довира к истории

в) реальнопараметры выбирают двумя способами:

 с помощью интуиции



Подбираются таким образом, чтобы различия между исходным рядом и сглаженным было минимальным.

28. Метод сезонной декомпозиции.

Методом сезонной декомпозиции - для моделей адетивных и мульти пликативных - когда на значение параметра влияют, как тренд, цикличность так и случайная компонента в их определенном соотношении

Используется если модель имеет вид Х = Т + Е + S

или Х = Т * Е * S

Выходные данные:

временной ряд Х, n

На основе автокорелограмы построенной ранее делается вывод о периоде цокличности и модель ряда.

Наш вариант-модель имеет вид Х = Т + Е + S, период 12 месяцев.

Необходимо найти сезонную компоненту S, уравнения Т (t)

В результате получим модель которая будет учитывать все кроме случайности.

Алгоритм расчета:

Расчет сезонной компоненты.

1-й столбец -порядок соответствии с периодом (1 ... 12 1 ... 12 1 ... 12 ...)

2-й столбец -это дискретное время

3-й столбец Значение концентрации соответствующей данному времени

4-й столбец - скользяще среднее -значение 0,285 среднее арифметическое первых 12 значений, а дальше автозаполнения до 6 с конца.

5-й столбец -центрированное среднее -значение 0,290411 среднее арифметическое из двух 0,285 и 0,29583333, а дальше автозаполнения

6-й столбец -сезонна компонента -значение 0,059583333 находится как разница между 3-м и 5-м столбце.

После этого необходимо распределить по годам в соответствии с 1-го столбца

Распределяя значение за 4 года до 6 столбца заносим среднее значение за каждый месяц. Далее находим сумму всех компонент. Должно быть 0. Но если получилась цифра отличная от 0 (0,01777778), то необходимо разделить ее на размер периода (12) = 0,0014814, и заполнить 7 столбец следующим образом -от 6 столбца отнять 0,0014814.

7 столбец и есть сезона компонента. запишем ее в более доступной форме.

28. Проверка модели временного ряда на адекватность.

Математическая модель процесса содержания свинца в верхнем слое почвы имеет вид: Х=Т+S, где

Т=t+7.235 (свое уравнение)-тренд компонент

S-сезонная компонента.

Проверка на адекватность:

А) значение R2. чем больше R2, тем лучше. Если же значение R2 почти одинаковые следует выбрать то уравнение, которое является простым.

Б)анализ данных-регрессия

В)Нахождение погрешности Е: =ABS((v-v)/v)*100

28. Прогноз временных рядов показателей экологических систем.

Пусть временный ряд имеет модель xt=f(t)

В результате точечный прогноз. На основании данных можно построие=ть доверительные интервалы для прогноза P{x1t<=xt<=x2t}=0.95