Интервальные оценки параметров распределения

Интервальной называют оценку, которая задается интервалом, покрывающим оцениваемый параметр генеральной совокупности. Доверительным называется интервал (,), который с заданной вероятностью  покрывает оцениваемый параметр генеральной совокупности. Вероятность  попадания оцениваемого параметра в доверительный интервал (,) называется доверительной вероятностью.

Доверительные интервалы для некоторых параметров распределения

Доверительный интервал для оценки математического ожидания a нормально распределенного количественного признака Х при известном среднем квадратическом отклонении  генеральной совокупности задается формулой:

, (1)

где  = 2Ф(t) – доверительная вероятность; – точность оценки.

Данная формула применяется для оценки математического ожидания М(Х) = а в двух случаях:

• если известно СКО (х)=;

• если СКО неизвестно, но объем выборки достаточно велик (n > 30). В этом случае в качестве  берут ее оценку S.

Доверительный интервал для оценки математического ожидания a нормально распределенного количественного признака Х при известном среднем квадратическом отклонении  генеральной совокупности задается формулой:

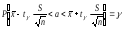, (2)

где t_ = t(,n) –находят по таблице приложения 3; 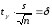– точность оценки.

Доверительный интервал для оценки среднего квадратического отклонения  нормально распределенного количественного признака Х задается формулой:

P{S(1 – q) <  <S(1+q)} =  , при q < 1 (3)

P{0 <  <S(1+q)} =  , при q > 1 . (4)

Здесь исправленное выборочное среднее квадратическое отклонение S служит оценкой для генерального среднего квадратического отклонения  ;

q=q(,n) – находят по таблице приложения 4; n – объем выборки;  – доверительная вероятность;

 = qS – точность оценки.

15. Статистическое сравнение экологических показателей.

Вопрос эффективности применения новой технологии сводится к проверке статистической гипотезе о равенстве двух средних (математических ожиданий) генеральных совокупностей. Для корректного решения необходимо убедиться в равенстве дисперсий указанных генеральных совокупностей.

Выдвинем основную и альтернативную гипотезы.

Определение. Нулевой гипотезой называют основную гипотезу и обозначают символом Но. Обычно нулевые гипотезы утверждают, что различие между сравниваемыми величинами (параметрами или функциями распределения) отсутствуют, а наблюдаемые отклонения объясняются лишь случайными колебаниями выборки.

Определение. Альтернативной (конкурирующей) называется гипотеза, конкурирующая с нулевой гипотезой в том смысле, что если нулевая гипотеза отвергается, то принимается альтернативная, которую обозначают символом Н1 .

Генеральных совокупностей

Имеем параметры выборок

по признаку Х: n1 – объем выборки; Sx2 – исправленная выборочная дисперсия;

по признаку У: n2 – объем выборки; Sу2 – исправленная выборочная дисперсия.

Пусть для определенности Sx2 > Sу2.

Требуется при заданном уровне значимости  сравнить дисперсии D(X) и D(Y) генеральных совокупностей.

Выдвинем основную и альтернативную гипотезы. Здесь рассмотрим два случая:

а) Н0: D(Х) = D(У) б) Н0: D(Х) = D(У)

Н1: D(Х)  D(У) Н1: D(Х)  D(У)

Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия (отношение большей дисперсии к меньшей):

Этот критерий является случайной величиной, которая подчиняется закону распределения Фишера–Снедекора.

Критические области и точки зависят от выдвинутых альтернативных гипотез H1 .

а) Н1: D(Х)  D(У)

Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Фишера–Снедекора (приложение 7)

Fкр=F(; k1; k2),

где  – заданный уровень значимости; k1 = n1 –1 - число степеней свободы большей исправленной дисперсии (Sx2); k2 = n2 –1 - число степеней свободы меньшей исправленной дисперсии (Sy2).

Если в результате сравнения окажется Fнабл < Fкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Fнабл > Fкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.

б) Н1: D(Х)  D(У)

Критическая область является двусторонней. Критическая точка находится по таблице критических точек распределения Фишера–Снедекора (приложение 7)

Fкр=F(/2; k1; k2),

где  – заданный уровень значимости; k1 = n1 –1 - число степеней свободы большей исправленной дисперсии (Sx2); k2 = n2 –1 - число степеней свободы меньшей исправленной дисперсии (Sy2).

Если в результате сравнения окажется Fнабл < Fкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Fнабл > Fкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.