Сравнение двух математических ожиданий нормально распределенных генеральных совокупностей, дисперсии которых неизвестны и одинаковы

Имеем параметры выборок

по признаку Х: n1 – объем выборки; 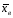– выборочная средняя; Sx2 – исправленная выборочная дисперсия;

по признаку У: n2 – объем выборки; – выборочная средняя; Sу2 – испр. выб. дисперсия.

Требуется при заданном уровне значимости  сравнить математические ожидания М(Х) и М(У) генеральных совокупностей.

Перед тем, как решать поставленную задачу, нужно убедиться, что дисперсии сравниваемых совокупностей равны (см. п. 4.1). Далее решение осуществляется следующим образом: выдвигается основная и альтернативная гипотезы. Рассмотрим три случая:

а) Н0: M(Х) = M(У) б) Н0: M(Х) = M(У) в) Н0: M(Х) = M(У)

Н1: M(Х)  M(У) Н1: M(Х) < M(У) Н1: M(Х)  M(У)

Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия

.

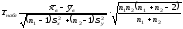Этот критерий является случайной величиной, которая подчиняется закону распределения Стьюдента с k = n1 + n2 – 2 степенями свободы.

Критические области и точки зависят от выдвинутых альтернативных гипотез H1 .

а) Н1: M(Х)  M(У)

Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, односторонняя критическая область)

tкр = t( ; k), где  – заданный уровень значимости.

Если в результате сравнения окажется Tнабл < tкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Tнабл > tкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.

б) Н1: M(Х) < M(У)

Критическая область является левосторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, односторонняя критическая область), только с отрицательным знаком

tкр = – t(; k), где  – заданный уровень значимости.

Если в результате сравнения окажется Tнабл< tкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Tнабл> tкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.

в) Н1: M(Х)  M(У)

Критическая область является двусторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, двусторонняя критическая область)

tкр = t(; k), где  – заданный уровень значимости.

Если в результате сравнения окажется Tнабл< tкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Tнабл > tкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.

16. Подбор закона распределения признака с помощью пакета «STATISTICА».

Закон распределения– функция (таблица, график, формула), позволяющая определять вероятность того, что случайная величина  Х  принимает определеное значение хi  или попадает в некоторый интервал. Если случайная величина  имеет данный закон распределения, то говорят, что она распределена по этому закону или подчиняется этому закону распределения.

1. Определить закон распределения.

2. По определенному закону посчитать вероятность попадания в интервал.

1. Работа в Статистике:

1)Создать файл (Spreadsheet)----->Открыть табл. ----->Изменить названия переменных----->

2)Для установления закона распределения заходим в меню «Статистика» -----> «Настройка распределения» -----> Probability calculator-----> *«continuos» (НСВ) ----->Выбрать переменные (Х) ----->Выбрать закон «Normal» ----->Выбрать график PLOT----->ОК

Получаем график, на котором показан нормальный закон распределения. На нем видим значения X² (хи-квадрат), чем меньше он, тем закон лучше подходит.

Р – чем больше, тем надежнее подходит этот закон.

Если Р<0,05 – закон отвергнуть

Р>0,05 – закон принять

Принимаем нормальный закон.

2. Прогноз. Вероятность попадания в интервал:

Р{x1<X<x2}=F(x2)-F(x1)

Для расчета в программе STATISTICA:

меню «Статистика» Probability calculator  Выбор распределения Z (normal) Расчет распределения вероятности (mean, st.dev., Х, Р)

При заданных данных: mean и st.dev. получим Х, Р.

17. Значение доверительного интервала для экологических прогнозов.

Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Доверительным интервалом параметра θ распределения случайной величины X с уровнем доверия 100%-p, порождённым выборкой (x1,…,xn), называется интервал с границами l(x1,…,xn) и u(x1,…,xn), которые являются реализациями случайных величин L(X1,…,Xn) и U(X1,…,Xn), таких, что

P(L≤θ≤U)=p.

Граничные точки доверительного интервала l и u называются доверительными пределами.

18. Оценка вероятности превышения концентрации загрязняющих веществ ПДК.

Формула вероятности показания Р{х1<X<x2}=F(x2)-F(x1)

В этом разделе нужно сделать 2 работы:

1)определить закон распределения

2)Посчитать вероятность попадания

-Создать файл

-«статистика»-Настройка распределения-НСВ/ДСВ-выбрать перен.-выбрать закон-график-расшифровка

3)сделаем таблицу, рассчитаем вероятность события

-придумаем вопрос:найти вероятность того, что пдк не превышает до определенного числа

- Р{х1<X<x2}=F(x2)-F(x1)

Р{х1>ПДК}=

Это значит практически достоверно, что пдк превышено или нет.

19. Проверка данных на аномальность (одномерная, двумерная и многомерная выборки).

Аномальные наблюдения – наблюдения, которые резко отличаются от остальных и не отражают общие свойства всей совокупности.

Одномерная:

Используют τ крит.

1. Расчет числовых характеристик (; D_в ; _в ; S² ; S ; Аs ; Ек; Mo ; Me) для всей выборки.

2.Рассчитывают для каждого наблюдения наблюдаемое значение критерия.

3. Проверка условия, где t крит– критическое значение, которое находится по таблице критических точек нашли критическое значение критерия:

t крит=t(α;n). α – вероятность ошибки прогноза=0,05; n – объем выборки.

Сравниваем:

· если значение τ набл < t крит, то это наблюдение не аномальное;

· если значение τ набл > t крит, то это наблюдение считается аномальным. Затем его удаляют из выборки, выборку пересчитывают и почищенную выборку вновь подвергают проверке на аномальность.

Двумерная:

По исходным данным строится корреляционное поле и выявляются на графике аномальные наблюдения, которое затем удаляют из выборки (тем самым создают «почищенный массив»). В Ексель: Вставка--->График--->Точечный

Многомерная:

Для множественной регрессии проверка на аномальность является из комбинации проверок на аномальность для одномерной и двумерной выборки.

Одномерной:

Проверяется каждый отдельный фактор с помощью τ крит.

Двумерной:

С помощью корреляционного поля след. Параметров: Х₁ и У, Х₂ и У, Х₂ и У, Х₄ и У.

Аномальные наблюдения из выборки удаляются и создается почищенный массив.

20. Статистическое моделирование процессов загрязнения автотранспортом окружающей городской среды с помощью регрессионного анализа.

Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) инезависимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной. Параметры модели настраиваются таким образом, что модель наилучшим образом приближает данные. Критерием качества приближения (целевой функцией) обычно является среднеквадратичная ошибка: сумма квадратов разности значений модели и зависимой переменной для всех значений независимой переменной в качестве аргумента.

Цели регрессионного анализа

1. Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)

2. Предсказание значения зависимой переменной с помощью независимой(-ых)

3.Определение вклада отдельных независимых переменных в вариацию зависимой

Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.

Строго регрессионную зависимость можно определить следующим образом. Пусть Y,X1,X2,…,Xp — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений X1=x1,X2=x2,…,Xp=xp определено условное математическое ожидание

y(x1,x2,…,xp)=E(Y∣X1=x1,X2=x2,…,Xp=xp) (уравнение регрессии в общем виде),

то функция y(x1,x2,…,xp) называется регрессией величины Y по величинам X1,X2,…,Xp, а её график — линией регрессии Y по X1,X2,…,Xp, илиуравнением регрессии.

Зависимость Y от X1,X2,…,Xp проявляется в изменении средних значений Y при изменении X1,X2,…,Xp. Хотя при каждом фиксированном наборе значений X1=x1,X2=x2,…,Xp=xp величина Y остаётся случайной величиной с определённым распределением.

Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение Y при изменении X1,X2,...,Xp, используется средняя величина дисперсии Y при разных наборах значений X1,X2,...,Xp (фактически речь идет о мере рассеяния зависимой переменной вокруг линии регрессии).

21. Парная регрессия. Формулы. Расчеты на ЭВМ.

Построение модели парной регрессия (или однофакторная модель) заключается в нахождении уравнения связи двух показателей у и х, т.е. определяется как повлияет изменение одного показателя на другой.

Уравнение модели парной регрессии можно записать в общем виде:

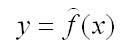
где у — зависимый показатель (результативный признак);

х — независимый, объясняющий фактор.

У=а₀+а₁*Х

а0, а1 – параметры ур-я, не меняются для одной модели, Х и У – меняются.

В Ексель: