
- •35 Вопрос:
- •36 Вопрос:
- •37 Вопрос:
- •39 Вопрос:
- •40 Вопрос:
- •41 Вопрос:
- •42 Вопрос:
- •43 Вопрос:
- •44 Вопрос:
- •45 Вопрос:
- •12.1. Несобственные интегралы по неограниченному промежутку
- •46 Вопрос:
- •47 Вопрос:
- •49 Вопрос:
- •50 Вопрос:
- •51 Вопрос:
- •52 Вопрос:
- •Связь с градиентом
- •53 Вопрос:
- •54 Вопрос:
- •Дифференциал высшего порядка функции одной переменной[править]
- •Дифференциал высшего порядка функции нескольких переменных[править]
- •55 Вопрос:
- •Необходимые условия существования локальных экстремумов [править]
- •Достаточные условия существования локальных экстремумов [править]
- •56 Вопрос:
- •57 Вопрос: Теорема об обратной функции.
54 Вопрос:
Дифференциалом порядка n,
где n
> 1,
от функции ![]() в некоторой точке называется дифференциал
в этой точке от дифференциала порядка (n —
1),
то есть
в некоторой точке называется дифференциал
в этой точке от дифференциала порядка (n —
1),
то есть
![]() .
.
Дифференциал высшего порядка функции одной переменной[править]
Для
функции, зависящей от одной переменной ![]() второй и третий дифференциалы выглядят
так:
второй и третий дифференциалы выглядят
так:
![]()
![]()
Отсюда
можно вывести общий вид дифференциала n-го
порядка от функции ![]() :
:
![]()
При
вычислении дифференциалов высших
порядков очень важно, что ![]() есть
произвольное и не зависящее от
есть
произвольное и не зависящее от ![]() ,
которое при дифференцировании по
,
которое при дифференцировании по ![]() следует рассматривать как постоянный
множитель.
следует рассматривать как постоянный
множитель.
Дифференциал высшего порядка функции нескольких переменных[править]
Если
функция ![]() имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так:
имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так: ![]() .
.
![]()
![]()
![]()
![]()
Символически
общий вид дифференциала n-го
порядка от функции ![]() выглядит
следующим образом:
выглядит
следующим образом:
![]()
где ![]() ,
а
,
а ![]() произвольные
приращения независимых
переменных
произвольные
приращения независимых
переменных ![]() .
Приращения
.
Приращения ![]() рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифференциала к следующему.
Сложность выражения дифференциала
возрастает с увеличением числа переменных.
рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифференциала к следующему.
Сложность выражения дифференциала
возрастает с увеличением числа переменных.
С помощью дифференциалов, функция
 при условии существования её (n
+ 1) первых
производных может быть представлена
по формуле
Тейлора:
при условии существования её (n
+ 1) первых
производных может быть представлена
по формуле
Тейлора:
для функции с одной переменной:
![]() ,
,
![]() ;
;
для функции с несколькими переменными:
![]() ,
, ![]()
Если первый дифференциал равен нулю, а второй дифференциал функции
 явлется положительно определённым
(отрицательно определенным), то точка
явлется положительно определённым
(отрицательно определенным), то точка 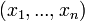 является точкой строгого минимума
(соответственно строгого максимума);
если же второй дифференциал функции
является точкой строгого минимума
(соответственно строгого максимума);
если же второй дифференциал функции 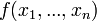 является неопределённым, то в точке
является неопределённым, то в точке 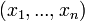 нетэкстремума.
нетэкстремума.
55 Вопрос:
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Пусть
дана функция ![]() и
и ![]() —
внутренняя точка области определения
—
внутренняя точка области определения ![]() Тогда
Тогда
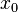 называется
точкой локального максимума функции
называется
точкой локального максимума функции  если
существует проколотая окрестность
если
существует проколотая окрестность  такая,
что
такая,
что
![]()
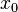 называется
точкой локального минимума функции
называется
точкой локального минимума функции 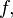 если
существует проколотая окрестность
если
существует проколотая окрестность  такая,
что
такая,
что
![]()
Если
неравенства выше строгие, то ![]() называется
точкой строгого локального максимума
или минимума соответственно.
называется
точкой строгого локального максимума
или минимума соответственно.
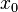 называется
точкой абсолютного (глобального)
максимума, если
называется
точкой абсолютного (глобального)
максимума, если
![]()
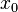 называется
точкой абсолютного минимума, если
называется
точкой абсолютного минимума, если
![]()
Значение
функции ![]() называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Необходимые условия существования локальных экстремумов [править]
Из леммы Ферма вытекает следующее:
Пусть
точка ![]() является
точкой экстремума функции
является
точкой экстремума функции ![]() ,
определенной в некоторой окрестности
точки
,
определенной в некоторой окрестности
точки ![]() .
.
Тогда
либо производная ![]() не
существует, либо
не
существует, либо ![]() .
.
(Математический Анализ. Том 1. Л. Д. Кудрявцев. Москва «Высшая Школа» 1973 г.)
Достаточные условия существования локальных экстремумов [править]
Пусть функция
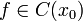 непрерывна
в
непрерывна
в 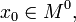 и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные 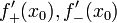 .
Тогда при условии
.
Тогда при условии
![]()
![]() является
точкой строгого локального максимума.
А если
является
точкой строгого локального максимума.
А если
![]()
то ![]() является
точкой строгого локального минимума.
является
точкой строгого локального минимума.
Заметим,
что при этом функция не дифференцируема
в точке ![]()
Пусть функция
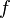 непрерывна
и дважды дифференцируема в точке
непрерывна
и дважды дифференцируема в точке 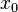 .
Тогда при условии
.
Тогда при условии
![]() и
и ![]()
![]() является
точкой локального максимума. А если
является
точкой локального максимума. А если
![]() и
и ![]()
то ![]() является
точкой локального минимума.
является
точкой локального минимума.
Пусть функция
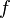 дифференцируема
дифференцируема 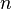 раз
в точке
раз
в точке 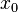 и
и 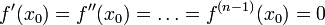 ,
а
,
а 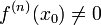 .
.
Если ![]() чётно
и
чётно
и ![]() ,
то
,
то ![]() -
точка локального максимума. Если
-
точка локального максимума. Если ![]() чётно
и
чётно
и ![]() ,
то
,
то ![]() -
точка локального минимума. Если
-
точка локального минимума. Если ![]() нечётно,
то экстремума нет.
нечётно,
то экстремума нет.
