
- •35 Вопрос:
- •36 Вопрос:
- •37 Вопрос:
- •39 Вопрос:
- •40 Вопрос:
- •41 Вопрос:
- •42 Вопрос:
- •43 Вопрос:
- •44 Вопрос:
- •45 Вопрос:
- •12.1. Несобственные интегралы по неограниченному промежутку
- •46 Вопрос:
- •47 Вопрос:
- •49 Вопрос:
- •50 Вопрос:
- •51 Вопрос:
- •52 Вопрос:
- •Связь с градиентом
- •53 Вопрос:
- •54 Вопрос:
- •Дифференциал высшего порядка функции одной переменной[править]
- •Дифференциал высшего порядка функции нескольких переменных[править]
- •55 Вопрос:
- •Необходимые условия существования локальных экстремумов [править]
- •Достаточные условия существования локальных экстремумов [править]
- •56 Вопрос:
- •57 Вопрос: Теорема об обратной функции.
42 Вопрос:
-
43 Вопрос:
Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0. (Для формулы средних прямоугольников равен 1).
Если
отрезок ![]() является
элементарным и не подвергается дальнейшему
разбиению, значение интеграла можно
найти по
является
элементарным и не подвергается дальнейшему
разбиению, значение интеграла можно
найти по
Формуле левых прямоугольников:
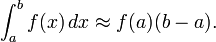
Формуле правых прямоугольников:

Формуле прямоугольников (средних):
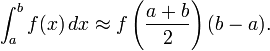
44 Вопрос:
Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольнымитрапециями. Алгебраический порядок точности равен 1.
Если
отрезок ![]() является
элементарным и не подвергается дальнейшему
разбиению, значение интеграла можно
найти по формуле
является
элементарным и не подвергается дальнейшему
разбиению, значение интеграла можно
найти по формуле
![]()
Это простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации можно оценить через максимум второй производной
![]()
Если
отрезок ![]() разбивается
узлами интегрирования и на каждом из
элементарных отрезков применяется
формула трапеций, то суммирование
дастсоставную
формулу трапеций
разбивается
узлами интегрирования и на каждом из
элементарных отрезков применяется
формула трапеций, то суммирование
дастсоставную
формулу трапеций
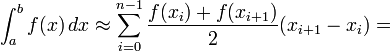
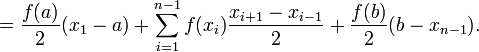
Метод трапеций быстро сходится к точному значению интеграла для периодических функций, поскольку погрешность за период аннулируется.
Метод может быть получен путём вычисления среднего арифметического между результатами применения формул правых и левых прямоугольников.
Метод пораболы:
Формула Симпсона (также Ньютона-Симпсона[1]) относится к приёмам численного интегрирования. Получила название в честь британского математикаТомаса Симпсона (1710—1761).
Суть
метода заключается в приближении
подынтегральной функции на
отрезке ![]() интерполяционным
многочленом второй
степени
интерполяционным
многочленом второй
степени ![]() ,
то есть приближение графика функции на
отрезке параболой. Метод Симпсона
имеет порядок
погрешности 4
и алгебраический
порядок точности 3.
,
то есть приближение графика функции на
отрезке параболой. Метод Симпсона
имеет порядок
погрешности 4
и алгебраический
порядок точности 3.
Формулой
Симпсона называется интеграл от
интерполяционного многочлена второй
степени на отрезке ![]() :
:
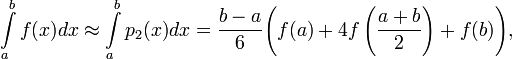
где ![]() ,
, ![]() и
и ![]() —
значения функции в соответствующих
точках (на концах отрезка и в его
середине).
—
значения функции в соответствующих
точках (на концах отрезка и в его
середине).
45 Вопрос:
12.1. Несобственные интегралы по неограниченному промежутку
(несобственные интегралы первого рода).
12.1.1. Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси
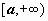 и
интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла
и
интегрируема по любому отрезку [a,b],
принадлежащему этой полуоси. Предел
интеграла  при
при 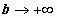 называется
несобственным интегралом
функции f(x) от a до
называется
несобственным интегралом
функции f(x) от a до 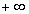 и
обозначается
и
обозначается 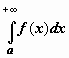 .
.
 Итак,
по определению,
Итак,
по определению,  .
Если этот предел существует и конечен,
интеграл
.
Если этот предел существует и конечен,
интеграл 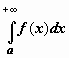 называется
сходящимся; если предел не существует
или бесконечен, интеграл называется
расходящимся.
называется
сходящимся; если предел не существует
или бесконечен, интеграл называется
расходящимся.
 Примеры:
1.
Примеры:
1. 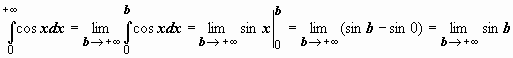 ;
этот предел не существует; следовательно,
исследуемый интеграл расходится.
;
этот предел не существует; следовательно,
исследуемый интеграл расходится. Признаки сравнения для неотрицательных функций. В этом разделе мы будем предполагать, что все подынтегральные функции неотрицательны на всей области определения. До сих пор мы определяли сходимость интеграла, вычисляя его: если существует конечный предел первообразной при соответствующем стремлении (
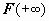 или
или 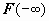 ),
то интеграл сходится, в противном случае
- расходится. При решении практических
задач, однако, важно в первую очередь
установить сам факт сходимости, и только
затем вычислять интеграл (к тому же
первообразная часто не выражается
через элементарные функции). Сформулируем
и докажем ряд теорем, которые позволяют
устанавливать сходимость и расходимость
несобственных интегралов от неотрицательных
функций, не вычисляя их.
),
то интеграл сходится, в противном случае
- расходится. При решении практических
задач, однако, важно в первую очередь
установить сам факт сходимости, и только
затем вычислять интеграл (к тому же
первообразная часто не выражается
через элементарные функции). Сформулируем
и докажем ряд теорем, которые позволяют
устанавливать сходимость и расходимость
несобственных интегралов от неотрицательных
функций, не вычисляя их.
 12.1.3.1.
Признак сравнения.
Пусть функции f(x) и g(x) интегрируемы
по любому отрезку [a,b] и
при
12.1.3.1.
Признак сравнения.
Пусть функции f(x) и g(x) интегрируемы
по любому отрезку [a,b] и
при 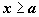 удовлетворяют
неравенствам
удовлетворяют
неравенствам 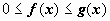 .
Тогда:
.
Тогда:
 если
сходится интеграл
если
сходится интеграл 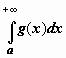 ,
то сходится интеграл
,
то сходится интеграл  ;
;
 если
расходится интеграл
если
расходится интеграл  ,
то расходится интеграл
,
то расходится интеграл 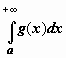
 (эти
утверждения имеют простой смысл: если
сходится интеграл от большей функции,
то сходится интеграл от меньшей функции;
если расходится интеграл от меньшей
функции, то расходится интеграл от
большей функции; в случаях, когда
сходится интеграл от меньшей функции
или расходится интеграл от большей
функции, никаких выводов о сходимости
второго интеграла сделать нельзя).
(эти
утверждения имеют простой смысл: если
сходится интеграл от большей функции,
то сходится интеграл от меньшей функции;
если расходится интеграл от меньшей
функции, то расходится интеграл от
большей функции; в случаях, когда
сходится интеграл от меньшей функции
или расходится интеграл от большей
функции, никаких выводов о сходимости
второго интеграла сделать нельзя).
 Док-во:
если
Док-во:
если  ,
,  ,
то функции
,
то функции 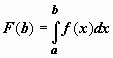 и
и 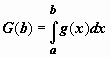 -
монотонно возрастающие функции верхнего
предела b (следствие
свойств аддитивности и интегрирования
неравенств). Монотонно возрастающая
функция имеет конечный предел тогда и
только тогда, когда она ограничена
сверху.
Пусть
-
монотонно возрастающие функции верхнего
предела b (следствие
свойств аддитивности и интегрирования
неравенств). Монотонно возрастающая
функция имеет конечный предел тогда и
только тогда, когда она ограничена
сверху.
Пусть 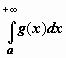 сходится. G(b) ограничена
сходится. G(b) ограничена 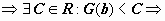
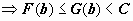 , F(b) ограничена,
т.е.
, F(b) ограничена,
т.е. 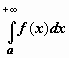 сходится.
Пусть
сходится.
Пусть 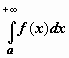 расходится
расходится  F(b) неограничена
F(b) неограничена  G(b) неограничена,
т.е.
G(b) неограничена,
т.е.  расходится.
расходится.
Критерий
Коши:
К.
к. сходимости несобственных интегралов:
пусть функция f определена на
полуинтервале ![]() принимает
на нем числовые значения и при
любом
принимает
на нем числовые значения и при
любом ![]() интегрируема
(по Риману или по Лебегу) на отрезке [ а,
с]. Для
того чтобы несобственный
интеграл
интегрируема
(по Риману или по Лебегу) на отрезке [ а,
с]. Для
того чтобы несобственный
интеграл
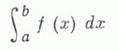
сходился,
необходимо и достаточно, чтобы для
любого ![]() существовало
такое
существовало
такое ![]() что
для всех
что
для всех ![]() удовлетворяющих
условию
удовлетворяющих
условию ![]() выполнялось
неравенство
выполнялось
неравенство
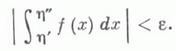
Аналогичным образом критерий формулируется и для несобственных интегралов других типов, а также обобщается на случай, когда функция f зависит от нескольких переменных и ее значения лежат в банаховом пространстве.
