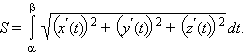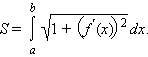35 Вопрос:

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

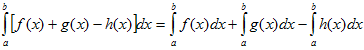
36 Вопрос:

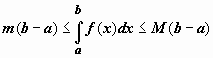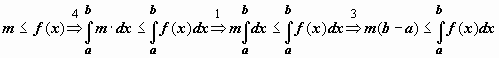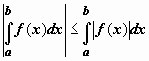5. Теоремы об оценке интеграла.   5.1. Если на отрезке [a,b] функция удовлетворяет неравенству , то .  Док-во. Докажем левое неравенство (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств): . Аналогично доказывается и правое неравенство.  5.2. Если функция f(x) интегрируема по отрезку [a,b], то .  Док-во. 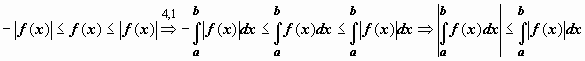.  6. Теорема о среднем. Если f(x) непрерывна на отрезке [a,b], то существует точка , такая что 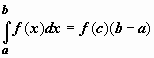.  Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда 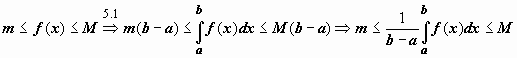. Число 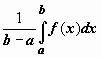заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка , такая что 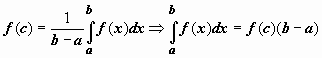.  Это свойство имеет простую геометрическую интерпретацию: если непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).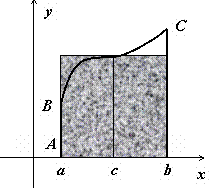

37 Вопрос:

Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то .  Док-во. Мы установили, что функция 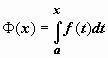- первообразная непрерывной f(x). Так как F(x) - тоже первообразная, то Ф(x) =F(x) +C. Положим в этом равенстве x = a. Так как 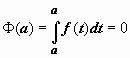, то 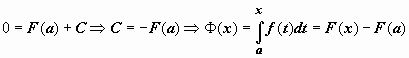. В равенстве 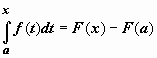переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x , верхний предел x обозначим b. Окончательно, 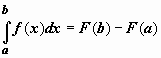.  Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом: (здесь читается как "подстановка от a до b"), поэтому формулу Ньютона-Лейбница обычно записывают так: 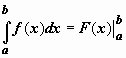.  Пример применения формулы Ньютона-Лейбница: .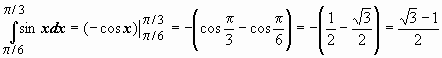

39 Вопрос:

 Длина дуги кривой.

Пусть задана кривая Тогда длина ее участка, ограниченного значениямиt = α и t = β выражается формулой 

В частности, длина плоской кривой, задаваемой на координатной плоскости OXY уравнением y = f (x), a ≤ x ≤ b, выражается формулой 

---Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:

40 Вопрос:

 Плоская фигура Q называется квадрируемой, если верхняя площадь этой фигуры совпадает с ее нижней площадью . При этом число называется площадью фигуры Q.

     Справедлива следующая теорема.

     Теорема 1. Для того чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа ε можно было указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q многоугольник, разность S_d - S_i площадей которых была бы меньшеε, S_d - S_i < ε.

     Доказательство.

     1) Необходимость. Пусть фигура Q квадрируема, т. е. . Так как и - точные верхняя и нижняя грани множеств {S_i} и {S_d}, то для любого числа ε > 0 можно указать такой вписанный в фигуру Q многоугольник, площадь S_i которого отличается от меньше чем на ε/2, т. е. P - S_i < ε/2. Для этого же ε > 0 можно указать такой описанный многоугольник, площадь S_d которого отличается от меньше чем на ε/2, т. е. S_d - P < ε/2. Складывая полученные неравенства, найдем, что S_d - S_i < ε.

     2) Достаточность. Пусть S_d и S_i - площади многоугольников, для которых S_d - S_i < ε. Так как , то . В силу произвольности ε отсюда вытекает, что . Таким образом, фигура квадрируема. Теорема доказана.

     Будем говорить, что граница плоской фигуры Q имеет площадь, равную нулю, если для любого положительного ε > 0 можно указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q многоугольник, разность S_d - S_i площадей которых меньше ε. Очевидно, теорему 1 можно также сформулировать следующим образом.

     для того чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы ее граница имела площадь, равную нулю.

     Замечание. Во всех приведенных нами рассуждениях вместо плоской фигуры можно рассматривать произвольное множество точек плоскости.

Критерием квадрируемости мы называем, как и в п. 4.5, сле­дующую теорему:

Множество М квадрируемо в том и только в том случае, если оно ограничено и его граница МГ есть ну ль-множеств о.

Доказательство. Предположим, что множество М огра­ничено и его граница Жг есть нуль-множество, и покажем, что

Ж—квадрируемая фигура. Для этого заметим, что если некото­рый квадрат ранга п задет множеством Ж, но не входит целиком в М, то он задет множеством Жг. Если бы это было не так, то он содержал бы по крайней мере одну точку, внутреннюю по от­ношению к Ж, и по крайней мере одну точку, внешнюю по отно­шению к Ж, и отрезок, соединяющий эти точки, все-таки пересе­кал бы множество Жг (см. п 4.4) в некоторой точке квадрата. Следовательно, число квадратов ранга п, задетых множеством М, но не входящих в Ж, не превышает числа квадратов ранга п, задетых множеством Жг, т. е.