3.Аксіоми вимірювання відрізків і кутів:

1. Кожний відрізок має певну довжину, більшу за нуль. Довжина відрізка дорівнює сумі довжин відрізків, на які він роз­бивається будь-якою своєю внутрішньою точкою.

2. Кожний кут має певну градусну міру, більшу за нуль. Розгорнутий кут дорівнює 180°. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.

3. Аксіоми відкладання відрізків і кутів:

   1. На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини, і тільки один.

   2. Від будь-якої півпрямої в даній півплощині можна від­класти кут із даною градусною мірою, меншою 180°, і тільки один.

   3. Хоч би який був трикутник, існує трикутник, що дорів­нює йому в заданому розміщенні відносно даної прямої.

4. Аксіома паралельності:

На площині через точку, що не належить прямій, проходить не більш як одна пряма, яка не перетинає дану пряму.

Аксіоми стереометрії:

1. Яка б не була площина, існують точки, що належать дій площині, і точки, що їй не належать.

2. Якщо дві різні площини мають спільну точку, то вони пере­тинаються по прямій.

3. Якщо дві різні прямі мають спільну точку, то через них проходить площина, і до того ж тільки одна.

Плоскі геометричні фігури

Одним з основних понять геометрії є поняття геометричної фігури, або просто фігури. Довільна непорожня множина точок називається геометричною фігурою.

Фігури поділяються на плоскі та просторові. Фігура називається плоскою, якщо всі її точки належать деякій площині (точка, пряма, відрізок, кут, площина).

Фігура називається просторовою, якщо не існує площини, якій би належали всі точки даної фігури. Найпростішою просторовою фігурою є фігура, що містить чотири точки, які не лежать в одній площині.

Надалі будемо вважати, що нам відомі такі фігури, як відрізок, півпряма, кут, а також деякі їх властивості.

Одним з основних понять геометрії є поняття геометричної

фігури, або просто фігури. Уявлення про неї можна отримати, розглядаючи предмети та звертаючи увагу лише на їх розміри і форму. Найпростішими геометричними фігурами є точка, пряма і площина, властивості яких описуються системою аксіом. На ос­нові теорії множин можна сформулювати означення геометричної фігури.

фігури. Довільна непорожня множина точок називається геомет­ричною фігурою.

Фігури поділяються на плоскі та просторові. Фігура назива­ються плоскою, якщо всі її точки належать деякій площині (точка, пряма, відрізок, кут, площина).

Фігура називається просторовою, якщо не існує площини, якій би належали всі точки даної фігури. Найпростішою просто­ровою фігурою є фігура, що містить чотири точки, які не лежать в одній площині.

Надалі будемо вважати, що нам відомі такі фігури, як відрі­зок, півпряма, кут, а також деякі їх властивості.

Серед найпростіших геометричних фігур чільне місце посі­дає ламана. Ламаною лінією (ламаною) називається фігура, яка є об'єднанням не менш як двох відрізків.

ЛаманоюА₁А₂ А₃……..А_n називають фігуру, яка складається із точок А_1,А_2, А_3,……..,А_n і з'єднуючих їхніх відрізків А₁А₂, А₂ А₃,…., А_n-1А_n . Точки А_1,А_2, А_3,……..,А_n називають вершинами ламаної, а відрізки А₁А₂, А₂ А₃,…., А_n-1А_n її ланками. Сусідні ланки ламаної не повинні лежати на одній прямій.

Ламана називається:

1) простою, якщо її несуміжні ланки не мають спільних точок;

2) замкненою, якщо її кінці збігаються

Про ламаних зображених на малюнку можна сказати, що: А₁А₂А₃ А₄ А₅ – проста; А₁А₂А₃А₄А₅ – замкнена ламана (вона не є простою, тому що має самоперетинання).

А₂

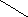
А₁ А₃ А₁ А₂

А₄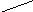

А₅ А₄ А₃

А₂ А₁

А₁ А₃ А₂

А₅ А₄ А

А₃

А₆ А₄

Довжиною ламаної називають суму довжин її ланок.

Відомо, що довжина ламаної не менше довжини відрізка, яке з’єднує її кінці. Поняття многокутника визначається, через ламану.

Ламана може бути як плоскою, так і просторовою фігурою. Замкнена ламана називається многокутником, при цьому ве­ршини ламаної називаються вершинами многокутника, а її ланки - сторонами многокутника. Зокрема, суміжні вершини ламаної, що задає многокутник, називаються суміжними вершинами много­кутника, а суміжні ланки - суміжними сторонами многокутника.

Многокутник називається простим, якщо ламана проста; опуклим, якщо ламана опукла. Відрізок, що з’єднує дві несуміжні вершини многокутника, називається його діагоналлю. Очевидно, що в трикутнику діаго­налей немає. В опуклому многокутнику кут, утворений двома його суміжними сторонами, називається кутом многокутника

. Будь-яка ламана, яка не перетинається сама з собою, обмежує пласку фігуру і ділить площину на дві частини – внутрішню і зовнішню по відношенню до цієї фігури.

Відрізки, які з’єднують дві несусідні вершини многокутника називають діагоналями многокутника.

Наприклад, діагоналями чотирикутника АВСД є відрізки АС, ВД.

А

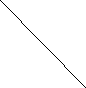
А В

В

F Д С Д

g Д С

Сума довжини всіх сторін даного многокутника називаються периметром многокутника. Многокутники бувають – випуклі і невипуклі.

Многокутник АВСД який зображено на малюнку – випуклий, а чотирикутник МNPK – випуклими не є, так як не лежить по одну сторону від прямої МК.

Відомо, що сума кутів випуклого n – кутника дорівнює 180⁰ (n-2).

Випуклий многокутник називається правильним, якщо у нього всі сторони і всі кути рівні.

Правильним трикутником є рівносторонній трикутник, правильним чотирикутником – квадрат.

У геометрії доводиться, що кожний простий многокутник розбиває множину точок площини, які не належать цьому много­кутнику, на дві підмножини так, що дві точки належать одній і тій же підмножині тоді і тільки тоді, коли їх можна з’єднати ла­маною, яка не перегне сторін даного многокутника. Одна з утворених підмножин характеризується тим, що вона містить деяку пряму, і цю підмножину називають зовнішньою областю многокутника. Друга підмножина називається внутрішньою областю многокутника. Названа властивість простого многокутника є частинним випадком так званої теореми Жордана. На рис. З внутрішні області многокутників заштри­ховано.

в геометрії здебільшого многокутником на­зивається лише простий многокутник, а також часто під много­кутником розуміють об’єднання многокутника з його внугрішньою областю.

Різниця між цими двома поняттями полягає в тому, що в першому випадку многокутник розглядається як лінія, а в другому - як частина площини, і тоді його називають плоским многоку­тником. Опуклий многокутник називається правильним, якщо в нього всі кути та всі сторон рівні між собою.