
лекции ММ ОМД
.pdf1. Математические модели и методы их реализации.
Часто возникает необходимость, как в самой математике, так и ее приложениях в разнообразных областях получать решения математических задач в числовой форме. (Для представления решения в графическом виде также требуется предварительно вычислять его значения.) При этом для многих задач известно только о существовании решения, но не существует конечной формулы, представляющей ее решение. Даже при наличии такой формулы ее использование для получения отдельных значений решения может оказаться неэффективным. Наконец, всегда существует необходимость решать и такие математические задачи, для которых строгие доказательства существования решения на данный момент отсутствуют.
Во всех этих случаях используются методы приближенного, в первую очередь численного решения. Методы численного решения математических задач всегда составляли неотъемлемую часть математики и неизменно входили в содержание естественноматематического и инженерного образования. Как самостоятельная математическая дисциплина вычислительная математика оформилась в начала 20-го века. К этому времени в основном были разработаны разнообразные, достаточно эффективные и надежные алгоритмы приближенного решения широкого круга математических задач, включающего стандартный набор задач из алгебры, математического анализа и дифференциальных уравнений.
Прогресс в развитии численных методов способствовал постоянному расширению сферы применения математики в других научных дисциплинах и прикладных разработках, откуда в свою очередь поступали запросы на решение новых проблем, стимулируя дальнейшее развитие вычислительной математики. Метод математического моделирования, основанный на построении и исследовании математических моделей различных объектов, процессов и явлений и получении информации о них из решения связанных с этими моделями математических задач, стал
1
одним из основных способов исследования в так называемых точных науках.
Параллельно с развитием численных методов шла разработка инструментальных средств вычислений, представлявших собой различные механические, а затем электромеханические устройства для выполнения арифметических операций. Причем прогресс в области инструментальных средств не оказывал заметного влияния на ход развития методов вычислений. Принципиальным образом ситуация изменилась со середины нашего столетия, когда было осуществлено изобретение электронных вычислительных машин. В результате появления ЭВМ скорость выполнения вычислительных операций выросла в миллионы раз, что позволило решить широкий круг бывших до этого практически не решаемыми математических задач. Широкое внедрение ЭВМ в практику научных и технических расчетов потребовало интенсивного развития методов численного решения самых разных математических задач, причем методов, рассчитанных на реализацию их именно на ЭВМ. Это связано с тем, что часть из ранее использовавшихся алгоритмов численного решения неэффективна при реализации на ЭВМ, а некоторые просто непригодны для такого использования.
2. Технология вычислительного эксперимента.
Современной формой метода математического моделирования, базирующейся на мощной вычислительной базе в виде ЭВМ и программного обеспечения, реализующего алгоритмы численного решения, является вычислительный эксперимент, рассматриваемый как новый теоретический метод исследования различных явлений и процессов. Этот теоретический метод включает существенные черты методологии экспериментального исследования, но эксперименты выполняются не над реальным объектом, а над его математической моделью, и экспериментальной установкой является ЭВМ.
Технологическая цепочка вычислительного эксперимента включает в себя следующие этапы:

 построение математической модели исследуемого объекта (сюда же относится и анализ модели, выяснение корректности поставленной математической задачи;
построение математической модели исследуемого объекта (сюда же относится и анализ модели, выяснение корректности поставленной математической задачи;
 построение вычислительного алгоритма - метода приближенного решения поставленной задачи и его обоснование;
построение вычислительного алгоритма - метода приближенного решения поставленной задачи и его обоснование;
программирование алгоритма на ЭВМ и его тестирование;  проведение серии расчетов с варьированием определяющих
проведение серии расчетов с варьированием определяющих
параметров исходной задачи и алгоритма; анализ полученных результатов;
Каждый из этих этапов допускает возврат к любому из предыдущих с целью его уточнения и корректировки.
В данном курсе рассматриваются вопросы, связанные со вторым этапом вычислительного эксперимента. Во многих случаях вычислительный алгоритм решения сложной задачи строится из набора базовых компонент, представляющих собой алгоритмы решения некоторых стандартных математических задач. Изучение численных методов решения этих задач - необходимый элемент овладения современной технологией математического моделирования.
При этом идея модели лежит в основе того, что можно назвать методом вычислительной математики. Как правило, алгоритмы приближенного решения базируются на том, что исходная математическая задача заменяется (аппроксимируется) некоторой более простой или чаще последовательностью более простых задач. Решение этих более простых задач трактуется как приближенное решение задачи исходной. Т.е. фактически используется некоторая модель исходной задачи.
3. Источники и классификация погрешностей. Погрешности данных, метода и вычислений
Почти всегда используемые на практике решения математических задач имеют некоторые погрешности.
Погрешность решения задачи обуславливается следующими причинами:
2
А) Математическое описание задачи является неточным, в частности, неточно заданы исходные данные описания.
Б) Применяемый для решения метод часто не является точным: получение точного решения задачи требует неограниченного или неприемлемо большого числа арифметических операций, и поэтому вместо получения точного решения приходится прибегать к приближенному.
При выполнении арифметических операций на ЭВМ или любым другим образом, как правило, производятся округления. (Это же относится к вводу чисел в память ЭВМ и выводу полученных результатов.)
Погрешности, соответствующие этим причинам, называются: неустранимая погрешность, погрешность метода, вычислительная погрешность.
4. Абсолютная и относительная погрешности вычисления
Если 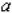 - точное значение некоторой величины, а
- точное значение некоторой величины, а 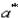 - известное приближение к нему, то абсолютной погрешностью приближения
- известное приближение к нему, то абсолютной погрешностью приближения
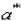 называют обычно некоторую величину
называют обычно некоторую величину 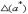 , про которую известно, что она удовлетворяет неравенству:
, про которую известно, что она удовлетворяет неравенству:
Относительной погрешностью называют некоторую величину 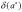 , про которую известно, что она удовлетворяет неравенству:
, про которую известно, что она удовлетворяет неравенству:
Относительную погрешность часто выражают в процентах. Она дает более точное представление о величине ошибки, содержащейся в некоторой величине.
5. Погрешности арифметических операций. Погрешность вычисления значений функции.
Пусть 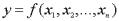 непрерывно дифференцируемая функция,
непрерывно дифференцируемая функция, 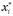 - приближенные значения ее аргументов, для которых
- приближенные значения ее аргументов, для которых
 - известные абсолютные погрешности.
- известные абсолютные погрешности.
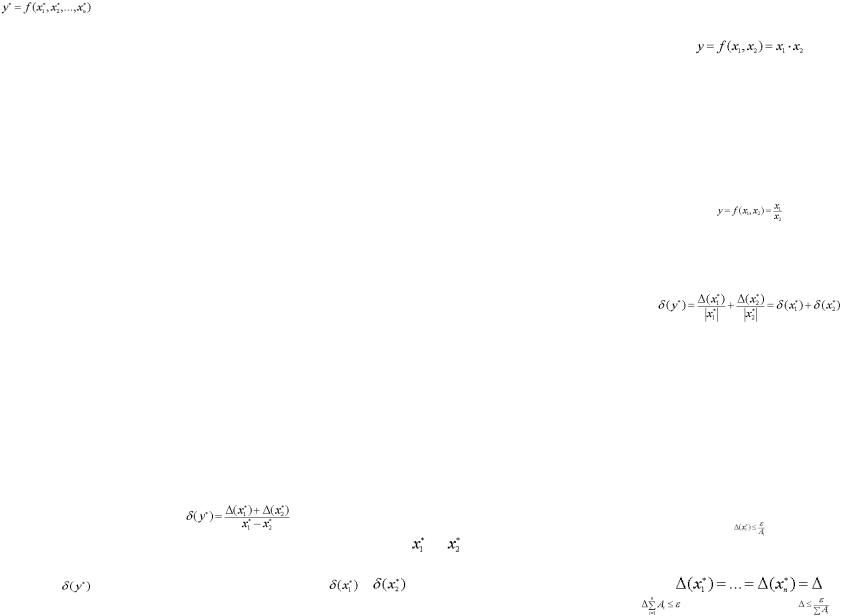
Для погрешности |
приближенного значения |
функции |
|
по |
формуле |
Лагранжа |
получаем |
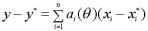 , где
, где 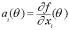
Заменяя 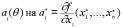 , получаем
, получаем 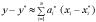 Оценка погрешности соответственно:
Оценка погрешности соответственно:
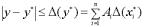 , где
, где 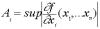
или 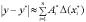 , где
, где 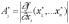
6. Погрешности арифметических операций. Погрешность суммы
Пусть задана функция 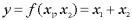
Тогда 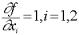 ,
, 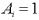 .
.
Для абсолютной погрешности получаем
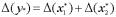 .
.
Относительная погрешность
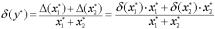 .
.
Пусть  ,
, 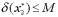 , тогда
, тогда 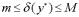 , т.е. при сложении приближенных величин относительная погрешность не возрастает.
, т.е. при сложении приближенных величин относительная погрешность не возрастает.
7. Погрешности арифметических операций. Погрешность разности
Пусть задана функция 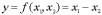 Тогда аналогично предыдущему абсолютная погрешность
Тогда аналогично предыдущему абсолютная погрешность
 .
.
Для относительной погрешности имеем формулу
|
|
. |
|
|
Отсюда следует, что если приближенные значения |
и |
|||
близки друг к другу, то |
относительная |
погрешность их |
||
разности |
может оказаться |
намного больше |
и |
. |
3
8. Погрешности арифметических операций. Погрешность произведения
Пусть задана функция
Тогда абсолютная погрешность
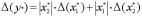 .
.
Относительная погрешность
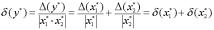 .
.
9. Погрешности арифметических операций. Погрешность частного
Пусть задана функция
Тогда абсолютная погрешность
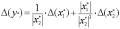 .
.
Относительная погрешность
10. Погрешности арифметических операций. Обратная задача оценки погрешности
Иногда возникает задача определения допустимой погрешности аргументов, при которой погрешность значений функции будет не более заданной величины 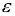 .
.
Используем ранее полученное неравенство
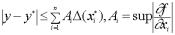 .
.
Должно быть 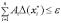 .
.
При n=1 вопрос решается однозначно:
При n>1 возможны разные подходы:
А) Считать погрешности всех аргументов одинаковыми
Тогда получаем |
, следовательно |

Б) Считать, что вклад погрешности каждого аргумента в погрешность результата одинаков. 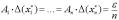 , тогда
, тогда
Если для разных аргументов достижение определенной точности их задания существенно различается, то можно ввести функцию стоимости 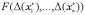 затрат на задание точки
затрат на задание точки 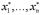 с заданными абсолютными погрешностями
с заданными абсолютными погрешностями 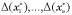 и искать ее минимум в области
и искать ее минимум в области
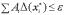 ,
, 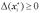
11. Электромагнитные явления
Как было показано ранее, основой САПР является моделирование проектируемых объектов. Рассмотрим теперь основные физические характеристики и математические модели, объясняющие принцип действия электротехнических устройств.
Работа электротехнических устройств, таких, как электродвигатели, трансформаторы, коммутационная аппаратура (контакторы), определяется одновременно многочисленными факторами.
Hа стадии моделирования основное место отводится задачам электромагнетизма, которые в свою очередь очень тесно связаны с тепловыми явлениями, определяющими основные требования к конструкции (нагревом, потерями и т. д.) Что касается механики объекта, то именно она позволяет определять окончательные характеристики конструируемых прототипов, причем материалы, из которых они изготавливаются, работают на пределе своих возможностей.
Электромагнетизм, термодинамика и механика — три обширные теоретические дисциплины, на базе которых с помощью САПР моделируются электротехнические устройства.
Рассмотрим с различныe модели и их применение для проектирования наиболее распространенных электротехнических устройств. Затем покажем, как современные средства информатики позволяют решать принципиальные задачи, возникающие при использовании этих моделей. Рассмотрим также
4
методы конечных разностей и конечных элементов, лежащие в основе вычислительных методов большинства современных САПР.
Действие электрического или магнитного поля (или их совокупности) определяет работу вращающихся машин, трансформаторов и контакторов высокого или низкого напряжения. Зная эти поля, можно установить для любого электромагнитного устройства их интегральные характеристики как в установившемся, так и в переходном режимах, зная величину магнитного поля, можно рассчитать значения потока, ЭДС (в генераторах), вращающего момента (в двигателях), силы притяжение или отталкивания (в контакторах), потери от собственных или наведенных токов и т. д.
Возрастающая сложность устройств, повышение требований, которым они должны удовлетворять, постоянное совершенствование аппаратуры затрудняют использование упрощенных гипотез. Таким образом, становится более трудным выбор подходящей модели.
12. Общая модель Максвелла Все электромагнитные явления, которые рассматриваются при
анализе классических электрогехнических устройств, описываются уравнениями Максвелла в частных производных. Обычно используемые величины скоростей и частот позволяют полностью пренебречь токами смещения. Тогда получим следующую общую модель:

где Е—вектор напряженности электрического поля; D— вектор электрической индукции; Н—вектор напряженности магнитного поля; В—вектор магнитной индукции; J—плотность тока; — объемная плотность заряда; Вr—вектор индукции остаточной намагниченности; 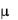 — магнитная проницаемость;
— магнитная проницаемость; 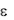 — диэлектрическая проницаемость;
— диэлектрическая проницаемость; 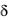 — удельная электрическая проводимость.
— удельная электрическая проводимость.
Примечание. В зависимости от используемых материалов 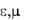
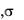 могут быть либо скалярами, как в случае изотропных материалов, либо тензорами, позволяющими учесть анизотропию, часто встречающуюся в электрических машинах.
могут быть либо скалярами, как в случае изотропных материалов, либо тензорами, позволяющими учесть анизотропию, часто встречающуюся в электрических машинах.
Эти уравнения полностью описывают все электромагнитные явления, однако, в настоящее время в большинстве случаев их нельзя решить непосредственно. С другой стороны, в конкретных рассматриваемых устройствах можно пренебречь некоторыми эффектами и тогда система уравнений распадается, принимая более простые формы.
5
12. Электростатическая модель
Эта модель справедлива для всех устройств, в которых электрическое поле создается зарядами, распределение и величина которых постоянны во времени.
Наиболее характерными задачами электростатики являются проектирование изоляторов и исследование поведения диэлектриков. В этом случае система уравнений Максвелла принимает следующий вид:
Соотношение rot Е = 0 позволяет определить такую вспомогательную функцию V, называемую скалярным потенциалом, что выполняется соотношение Е = —grad V.
Тогда задачу можно свести к следующему уравнению:
В большинстве случаев это уравнение можно решить современными численными методами.
Действительно, неизвестной величиной является скаляр V, значение которого необходимо вычислять в каждой точке; более того, решение существует и оно единственно, так как граничные условия изучаемой задачи выражаются в виде функции V или ее нормальной производной (что существует практически во всех случаях).
Обычно полагают, что потенциал на границе известен (условие Дирихле) или скалярные эквипотенциальные линии перпендикулярны границам (случай симметричных плоскостей или границы с идеальным диэлектриком). В этом случае нормальная производная дV/дп полагается равной нулю. Наконец, имеется ряд задач, когда известна величина потока D, проходящего через границу, что соответствует условию дV/дп=К, где К—известная величина (условие Неймана). Если —константа, то задача существенно упрощается. Но решение задачи возможно также в случае, когда 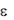 зависит от самого электрического поля
зависит от самого электрического поля

(уравнение становится нелинейным и должен быть известен закон изменения 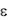 для выбранных материалов). В этом случае решение задачи довольно громоздкое, но методы решения определены раз и навсегда (метод Ньютона—Рафсона, который будет рассмотрен ниже, дает очень хорошие результаты). Наконец, если материал анизотропный,
для выбранных материалов). В этом случае решение задачи довольно громоздкое, но методы решения определены раз и навсегда (метод Ньютона—Рафсона, который будет рассмотрен ниже, дает очень хорошие результаты). Наконец, если материал анизотропный, 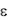 становится тензором и это обстоятельство также можно учесть, не усложняя решения задачи. И только при очень сложной геометрической форме объекта проектирования классические методы могут быть неприменимы, но это происходит только в случае сложных трехмерных объектов.
становится тензором и это обстоятельство также можно учесть, не усложняя решения задачи. И только при очень сложной геометрической форме объекта проектирования классические методы могут быть неприменимы, но это происходит только в случае сложных трехмерных объектов.
13. Скалярная магнитостатическая модель
В этой модели полагают, что токи в рассматриваемом объекте равны нулю и что поле не меняется во времени. Тогда система уравнений Максвелла принимает следующий вид:
Это случай устройств, в которых поле создается внешними и независящими от проектируемого устройства магнитодвижущими силами или постоянными магнитами, при этом справедлив закон
Соотношение rot Н = 0 предполагает, что существует некоторая функция ( , называемая скалярным потенциалом, такая, что
С учетом этого соотношения получаем уравнение
Его решение известно, хотя у инженеров, использующих эту модель, возникают дополнительные затруднения при составлении граничных условий.
В самом деле, необходимо знать значения полей на границах рассматриваемой области. Эти значения предварительно вычисляются и в этом случае приходится отказаться от учета влияния рассматриваемой области на внешнее поле. Рекомендуется тщательно проверять справедливость такого предположения для модели. При этом на исследуемой границе
6
задаются либо величины , которые легко вычисляются (если тангенциальную составляющую поля Н на границе можно считать равной нулю), либо величины нормальной производной, когда на границе известна нормальная составляющая д /дп поля В.
Наличие постоянного магнита существенно не усложнит эту модель, позволяющую учитывать нелинейные зависимости. В этом методе использование скалярного потенциала упрощает решение трехмерных задач, так как в каждой точке требуется определить только одну, а не три неизвестные величины, как в векторном случае. Поэтому по возможности лучше пользоваться им, а не векторной формулировкой, которая будет определена ниже.
14. Векторная магнитостатическая модель
Как и в предыдущей модели, полагаем, что магнитное поле создается источниками, не зависящими от времени. Производная дВ/дt равна нулю, при этом электрические Е и магнитные В поля являются независимыми. Однако в отличие от предыдущего случая в моделируемых объектах ток проводимости отличен от нуля.
Система уравнений Максвелла приобретает следующий вид:
Условие div В = 0 позволяет определить некоторую векторную функцию А такую, что
Эта функция называется векторным магнитным потенциалом
(чтобы функция была полностью определена, следует также определить значение ее дивергенции). Тогда добавляется условие (называемое калибровкой Кулона)
которое довольно просто реализуется, но не всегда имеет наилучшую форму и его следует видоизменять во избежание вычислительных затруднений, к которым оно приводит. В результате

получаем следующую систему уравнений:
к которым следует добавить соотношение, характеризующее свойства вещества
и выражающее нелинейную связь между полями В и Н вследствие насыщения магнитного поля (особенно в месте сужения магнитного потока).
Для этой модели граничные условия необходимо выразить через векторный потенциал. Как правило, приравнивают нулю тангенциальную составляющую А на границе, находящейся в бесконечности (т. е. достаточно удаленной, чтобы магнитную энергию можно было полагать равной нулю). На оси симметрии вращения накладывается условие А = 0, а в плоскостях магнитной и геометрической симметрии - условие дV/дп = 0, т. е. линии потока перпендикулярны этим плоскостям. В случае когда рассматриваемая область граничит с материалами, проницаемость которых можно считать много большей, чем проницаемость внутренних материалов (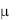 внешнее в 1000 раз превышает
внешнее в 1000 раз превышает 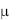 внутреннее), нормальную составляющую А, т. е. An, можно считать равной нулю.
внутреннее), нормальную составляющую А, т. е. An, можно считать равной нулю.
Теперь при наличии условий, определенных на границах, задача в частных производных получает единственное решение. Однако в противоположность предыдущему случаю, не* обходимо определить три неизвестные величины в каждой точке Ax, Ау, Аz . В трехмерной задаче это приводит к дорогостоящему решению очень громоздкой линейной системы уравнений; поэтому, когда рассматривается достаточно протяженная область, можно провести анализ сечения и тем самым свести исследование к решению двумерной задачи. В одном из таких случаев, когда токи, создающие магнитное поле, перпендикулярны рассматриваемой плоскости (это случай почти всех «протяженных» вращающихся машин), векторный потенциал имеет только одну составляющую.
7
С другой стороны, тогда условие div А = 0 выполняется автоматически.
15. Двумерная магнитостатическая модель .
Как и в предыдущей модели, полагаем, что магнитное поле создается источниками, не зависящими от времени. Производная дВ/дt равна нулю, при этом электрические Е и магнитные В поля являются независимыми. Однако в отличие от предыдущего случая в моделируемых объектах ток проводимости отличен от нуля.
Система уравнений Максвелла приобретает следующий вид:
Условие div В = 0 позволяет определить некоторую векторную функцию А такую, что
Эта функция называется векторным магнитным потенциалом
(чтобы функция была полностью определена, следует также определить значение ее дивергенции). Тогда добавляется условие (называемое калибровкой Кулона)
Если сечение проходит перпендикулярно оси Оz, то одно из уравнений в частных производных должно решаться в скалярной форме
При решении этой задачи используется та же методика, что и при рассмотрении уже встречавшихся ранее скалярных электро- и магнитостатических моделей. Современные методы позволяют использовать эту модель даже в тех случаях, когда —нелинейная функция В или —тензор; наличие магнита не создает каких-либо непреодолимых трудностей.
Если рассматриваемые области обладают симметрией вращения (индукционные нагреватели, сердечники трансформаторов и т. д.),

трехмерная задача также сводится к двумерной, а векторный потенциал имеет только одну составляющую A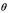 (перпендикулярную рассматриваемой плоскости) и уравнение принимает вид:
(перпендикулярную рассматриваемой плоскости) и уравнение принимает вид:
для которого автоматически выполняется условие калибровки divA=0.
В трехмерном случае решение для модели векторного магнитного потенциала получается более сложным: действительно, было показано, что соблюдение условия калибровки divA = 0 может привести к сложным проблемам сходимости. Поэтому предпочтение обычно отдается скалярной магнито-статической модели, которую мы рассматривали ранее.
Наконец, во всех моделях, рассматриваемых ранее, члены уравнений выражаются функциями токов, протекающих по проводникам. Эти члены должны быть известны либо в виде плотностей тока (предполагается идеальный генератор тока), либо в форме *gradV (предполагается идеальный генератор напряжения).
16. Электродинамическая модель
Эта модель используется при рассмотрении распределения тока в изолированных проводниках при постоянной разности потенциалов. В этом случае она определяется следующими уравнениями:
Условие rot E = 0 означает, что существует такой скалярный потенциал , что Е = - grad . Этот потенциал называется электрическим напряжением. Тогда следует решить уравнение
совместно с граничными условиями:
разность потенциалов между двумя поверхностями постоянна,
8
тогда потенциал определен на этих границах (условие Дирихле); нормальная производная потенциала , т е. д /дп равна нулю на границах проводников, окруженных изолятором (однородное
условие Неймана).
Эта модель почти не создает никаких дополнительных трудностей, а вычислительная техника позволяет использовать ее даже в сложных трехмерных случаях. Модель можно использовать и в случае, когда —тензорная величина (анизотропная проводимость).
Примечание. В случае когда к проводнику не приложена постоянная разность потенциалов, эта модель неприменима, так как переменное магнитное поле вызывает вихревые токи, которые изменяют общее распределение токов в проводнике. В силу этого эффекта изменяется кажущееся сопротивление проводника в зависимости от протекающего по нему тока (постоянного пли переменного). Тем не менее, если частота источника не высока, распределение переменных токов мало отличается от распределения постоянных токов. Действительно, можно полагать, что токи распределены в периферийной зоне проводников внутри «поверхностного слоя», расчетная толщина которого имеет порядок
где f—частота тока. Если размеры зоны больше размеров рассматриваемого проводника, то наша скалярная магнитостатическая модель дает удовлетворительную аппроксимацию. Именно поэтому в случае прохождения токов через толщу предпочтительнее использовать разделенные, а не сплошные проводники, поскольку их внутренняя часть для прохождения токов не используется.
17. Магнитодинамическая модель.
Данная модель применяется для описания электротехнических устройств, когда токи или напряжения источника меняются во времени.
Производная дB/дt уже не равна нулю, электрическое и

магнитное поле связаны между собой присутствием вихревых токов (или токов Фуко).
Чтобы представить электромагнитное поле в некоторой точке, одновременно воспользуемся векторным потенциалом ,(так как divB=0), определенным ранее, и скалярным потенциалом .
Поскольку
Это приводит к следующей модели:
Примечание 1. В уравнении (34) Jех—плотность тока (называемая током возбуждения), питающего рассматриваемое электротехническое устройство. Ток создается идеальным генератором тока. Чтобы использовать магнитодинамическую модель, необходимо знать величину этого тока. Примечание 2 Векторный потенциал нельзя определить с помощью только одного условия В = rot А, необходимо ввести его дивергенцию Выбирая дивергенцию, можно получить различные типы моделей.
18. Квадривекторная магнитодинамическая модель.
В наиболее сложном случае, когда заряды не равны нулю, необходимо вычислить функцию ср. Для этого нужно разделить систему уравнений (34) и (35), тогда условие калибровки
приведет к системе
Эта модель позволяет учитывать самые общие электромагнитные явления, хотя решение уравнений (37) и (38) довольно трудоемкое, так как в каждой точке вычисляется четыре величины Аx, Ау, Аz, . Кроме того, уравнения содержат и другие сложности: закон распределения неизвестных очень быстро
9
меняется на границе проводящей области в случае поверхностного эффекта, описанного выше; магнитная проницаемость сильно зависит от поля в ферромагнитных материалах (эффект насыщения); уравнения к тому же нелинейные и может возникнуть сложная задача сходимости. В заключение отметим, что в общем случае, и особенно в случае сложной трехмерной области, эту модель при современном уровне вычислительной техники рассчитать нельзя, что заставляет использовать упрощенные модели.
19. Нелинейная магнитодинамическая модель, выраженная через векторный потенциал.
Когда заряды равны нулю (это соответствует случаю почти всех классических индукционных устройств), функцию 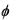 можно считать равной нулю в бесконечности и условие калибровки
можно считать равной нулю в бесконечности и условие калибровки
приводит к уравнению
которое совместно с условием на границе 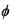 = 0 приводит к выводу, что функция
= 0 приводит к выводу, что функция 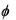 равна нулю повсюду. Тогда модель описывается уравнениями
равна нулю повсюду. Тогда модель описывается уравнениями
Теперь эта модель удобна для расчетов и вполне подходит для решения трехмерных задач, которое подробно рассматривается в работах Кулона. Однако, несмотря на это, решение модели все же зависит от производительности ЭВМ, используемых в современных САПР. Поэтому следует применять более простые модели, если они обеспечивают удовлетворительную аппроксимацию при заданной точности.
20. Линейная магнитодинамическая модель, выраженная через векторный потенциал.
В этой модели полагают, что магнитная проницаемость постоянна, более того, считают, что функция 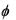 повсюду равна
повсюду равна

нулю (как и в предыдущем случае). Тогда имеем следующий оператор:
Если токи возбуждения Jex — переменные, то можно использовать представление Френеля для описания их изменения во времени. Использование комплексных чисел позволяет заменить
дифференцирование по времени, т. е. член |
дA/дt произведением |
j A, где j-мнимая единица (j2 =-1), а |
-круговая частота |
источника. Тогда получаем выражения |
|
Это представление можно использовать в трехмерных задачах, однако при этом требуется в каждой точке определить три неизвестные величины Ax, Ау, Аz, что увеличивает стоимость решения. Если позволяет геометрия, то использование таких моделей в случае двумерной задачи может привести к прекрасным результатам.
21. Двумерная магнитодинамическая модель, выраженная через векторный потенциал.
В случае объектов, достаточно протяженных или обладающих симметрией вращения, токи обычно направлены перпендикулярно рассматриваемой плоскости. При этом векторный потенциал имеет только одну составляющую (также перпендикулярную рассматриваемой плоскости) и условие div A = 0 выполняется автоматически. Тогда модель принимает вид
который содержит только одну неизвестную.
Такая модель особенно проста и эффективна и применяется довольно широко (при изучении асинхронных двигателей, нагревательных индукционных устройств, трансформаторов и т.
д.).
Примечание. Если —постоянная, то можно воспользоваться уравнением в комплексной форме
10
которое решается с приемлемой скоростью.
22. Линейная магнитодинамическая модель, выраженная через напряженность магнитного поля Н.
В этой модели ограничимся рассмотрением проводящих областей, помещенных в переменное магнитное поле. В этих областях наводятся токи и модель описывается уравнением
Определяя ротор от этого выражения, получаем
Особый интерес модель представляет при двумерном анализе, когда можно предположить, что индуцированные токи расположены в рассматриваемой плоскости. Действительно, в этом случае поле Н имеет только одну составляющую, перпендикулярную этой плоскости. Тогда уравнение принимает вид
В случае синусоидальных источников можно использовать уравнение в комплексной форме
Однако решение такого уравнения можно найти только тогда, когда известна величина поля на границе рассматриваемой области. Это заставляет объединить эту модель с каким-либо другим методом расчета, определяющим внешние поля, что часто осуществимо, если справедливо предположение, что внешние поля не изменяются при наличии исследуемой области. Тогда это сводится к пренебрежению эффектом, который электротехники называют реакцией вихревых токов в электрических машинах.
Эта модель достаточно эффективна, однако ее необходимо использовать осторожно с проверкой справедливости выдвинутых предположений.
23. Особенности моделирования электромагнитного поля переменного синусоидального тока и в движущихся областях.
Общее замечание, касающееся моделей в комплексной фор-
