4.Плотность распределения системы двух случайных величин.

Предположим, что функция распределения непрерывна и дважды дифференцируема, тогда смешанную частную производную функцииобозначим через:

.

Функция называется плотностью распределения системы непрерывных случайных величин . Зная плотность распределения, можем определить вероятность попадания случайной точкив произвольную область:

. (5.1)

Используя формулу (5.1), выразим функцию распределения системы через плотность распределения:

. (5.2)

Рассмотрим свойства плотности распределения системы двух случайных величин.

Свойство 1. Плотность распределения есть функция неотрицательная:

.

Свойство 2. Двойной несобствнный интеграл с бесконечными пределами от плотности распределения системы равен единице:

.

Пример 1. Плотность распределения системы двух случайных величин задана выражением

.

Найти . Определить функцию распределенияи найти вероятность попадания случайной точки в прямоугольник с вершинами,,и.

Решение. Пользуясь свойством 2 плотности распределения, найдем постоянную величину :

.

Следовательно, . Функцию распределенияопределяем по формуле (5.2):

.

Вероятность попадания случайной точки в заданный прямоугольник согласно формуле (5.1) равна

5. Условные законы распределения.

Пусть известна плотность распределения системы двух случайных величин. Используя свойства функций распределения, можно вывести формулы для нахождения плотности распределения одной величины, входящей в систему:

. (5.3)

Перейдем теперь к решению обратной задачи: по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. Как легко видеть, в общем случае эта задача неразрешима. Действительно, законы распределения отдельных случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они связаны между собой. С другой стороны, искомый закон распределения системы должен содержать все сведения о случайных величинах системы, в том числе и о характере связей между ними.

Таким образом, если случайные величины зависимы между собой, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения.

Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.

Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается , условная плотность распределения(мы записали условные законы распределения случайной величиныпри условии, что другая случайная величинаприняла определенное значение).

Плотностью распределения для случайной величины при условии, что случайная величинаприняла определенное значение (условной плотностью распределения) назовем величину

.

Аналогично, плотностью распределения для случайной величины при условии, что случайная величинаприняла определенное значение, назовем величину

.

Осюда получаем, что

,

или, с учетом формул (5.3),

,

.

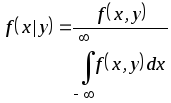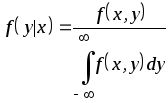Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,

,

6.Числовые характеристики условных законов распределения.

Для описания условных законов распределения мы можем использовать различные характеристики, подобно тому как мы имели для одномерных распределений.

Наиболее важной характеристикой является условное математическое ожидание.

Условным математическим ожиданием дискретной случайной величины при(- определенное возможное значение случайной величины) называется сумма произведений возможных значенийна их условные вероятности:

.

Для непрерывных случайных величин

,

где - условная плотность распределения случайной величиныпри.

Аналогично, условным математическим ожиданием дискретной случайной величины приназывается сумма произведений возможных значенийна их условные вероятности:

.

Для непрерывных случайных величин

,

где - условная плотность распределения случайной величиныпри.

Подобным образом вводятся условные дисперсии и условные моменты более высоких порядков.