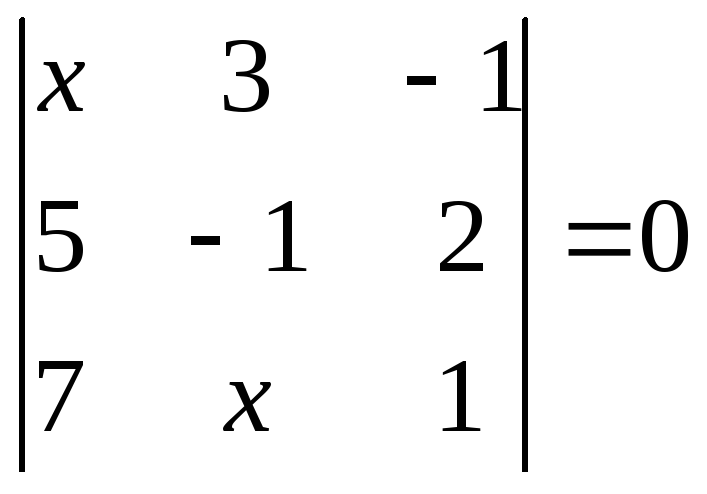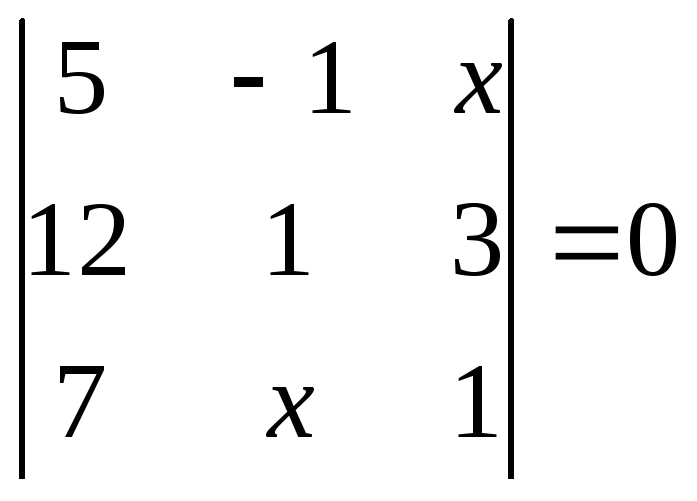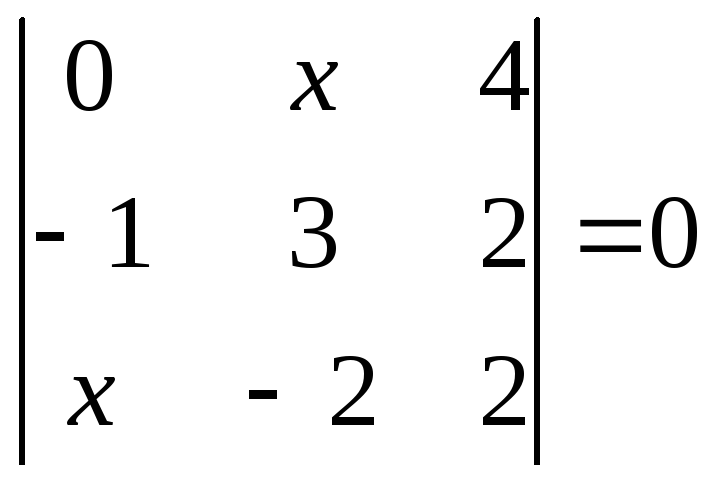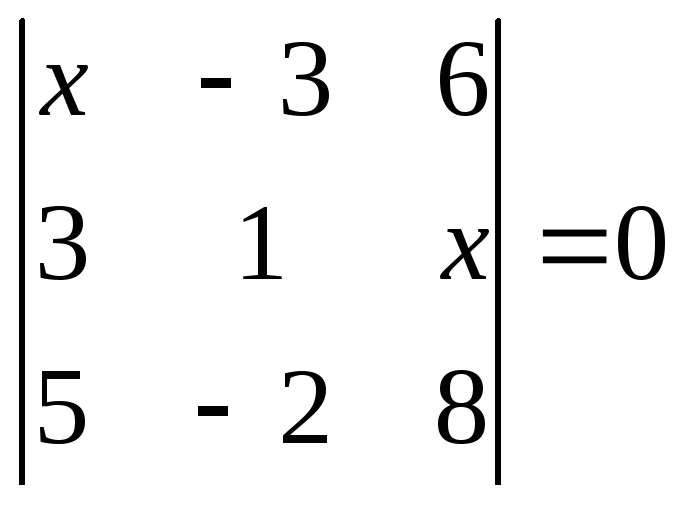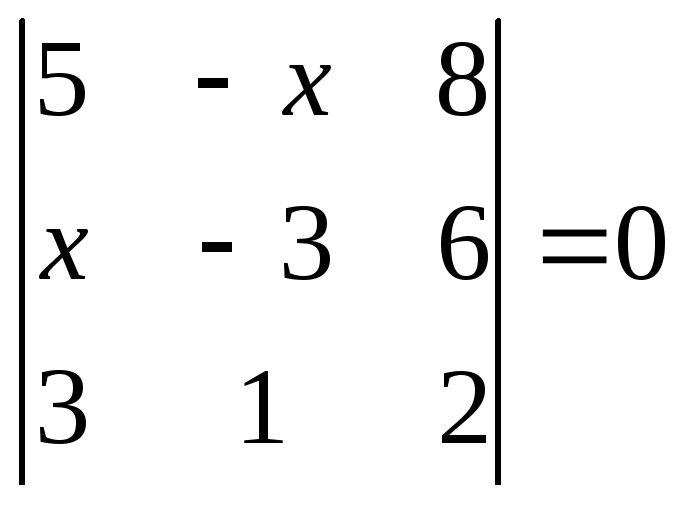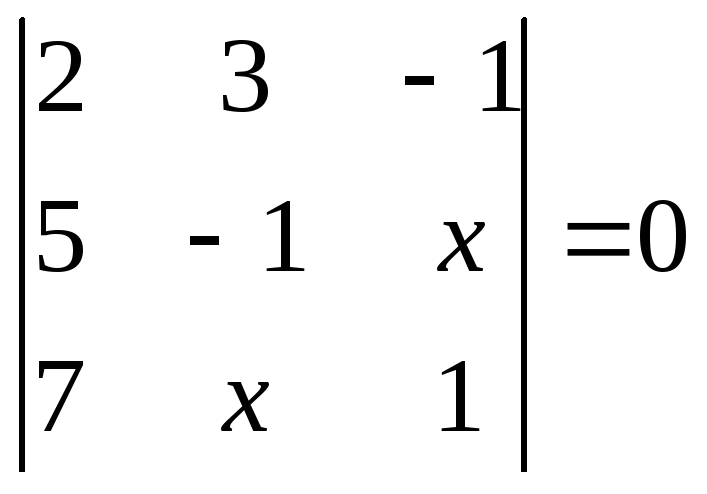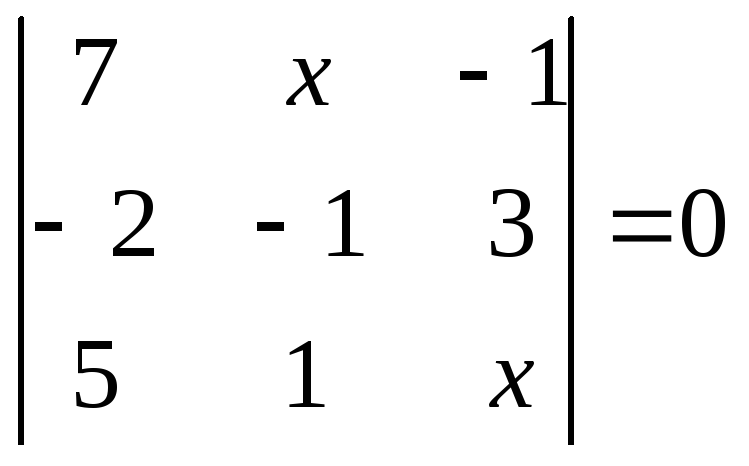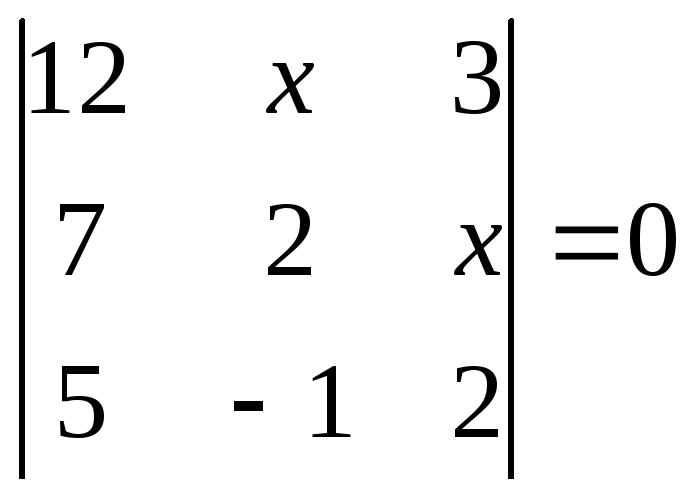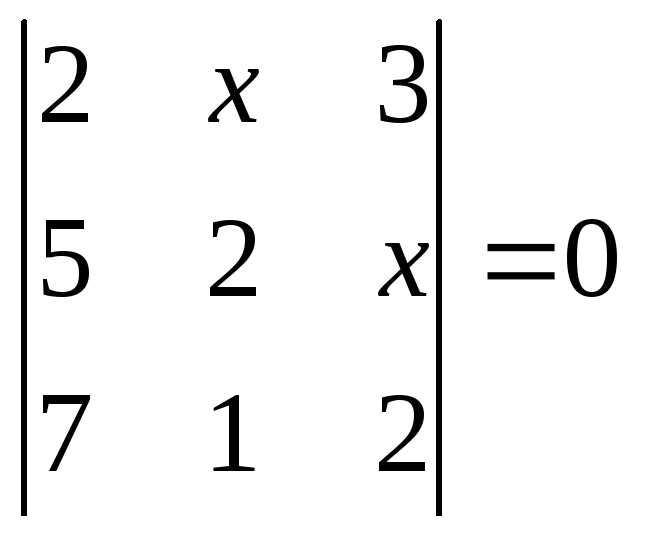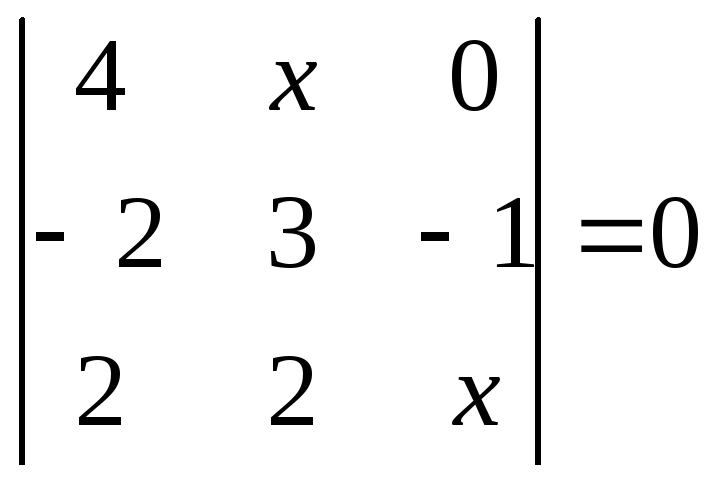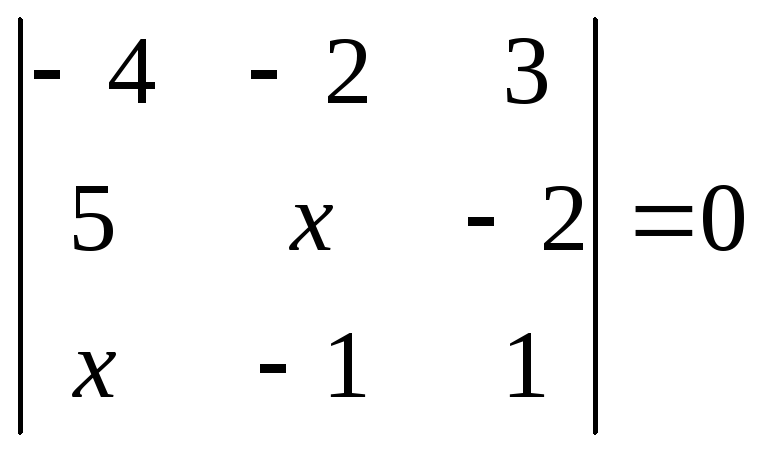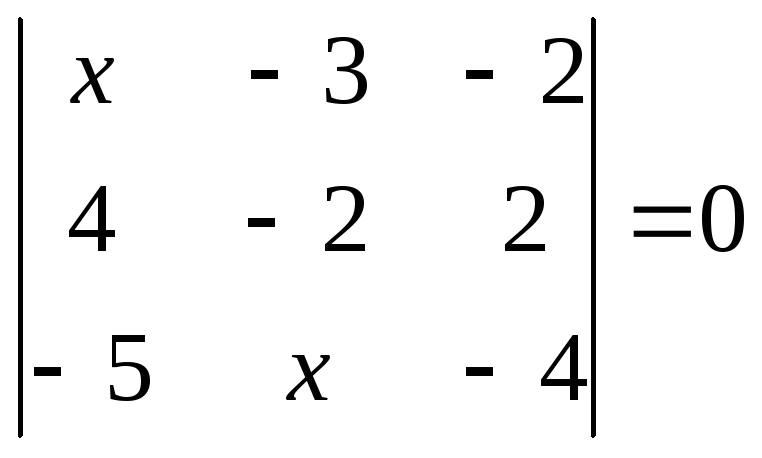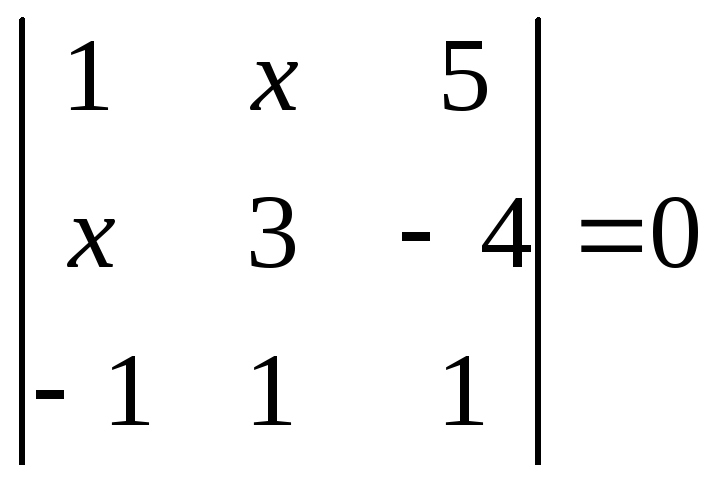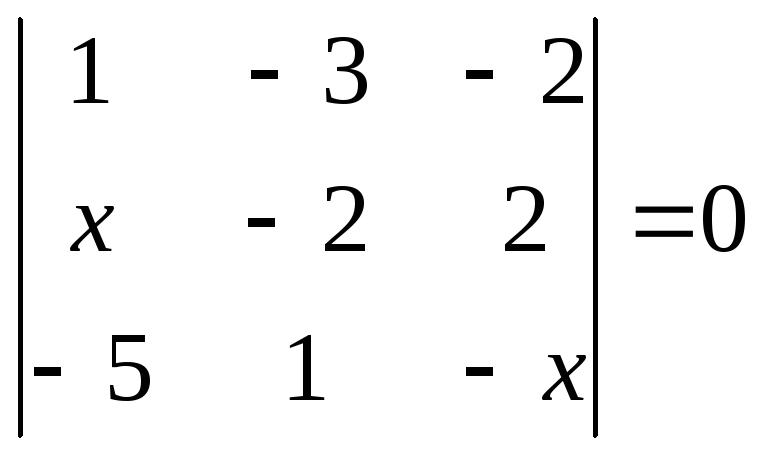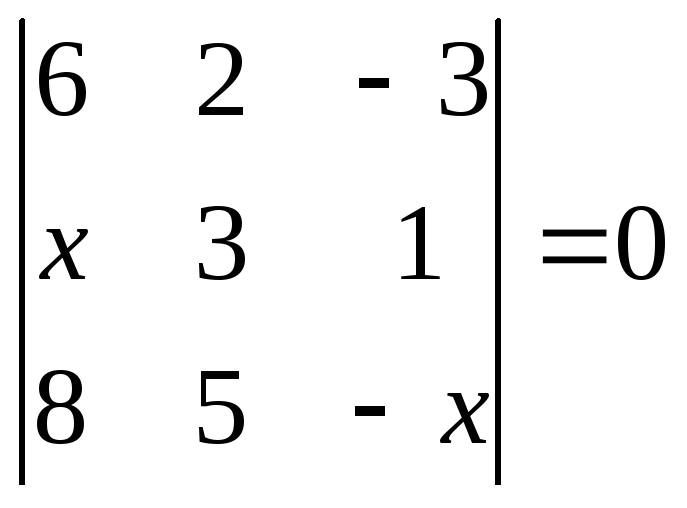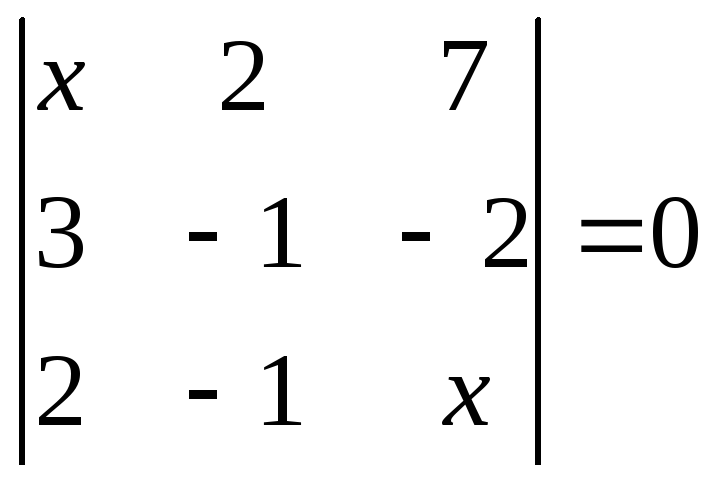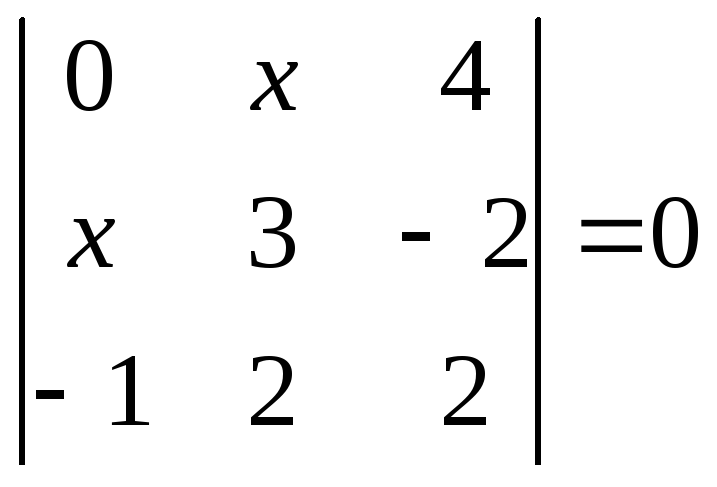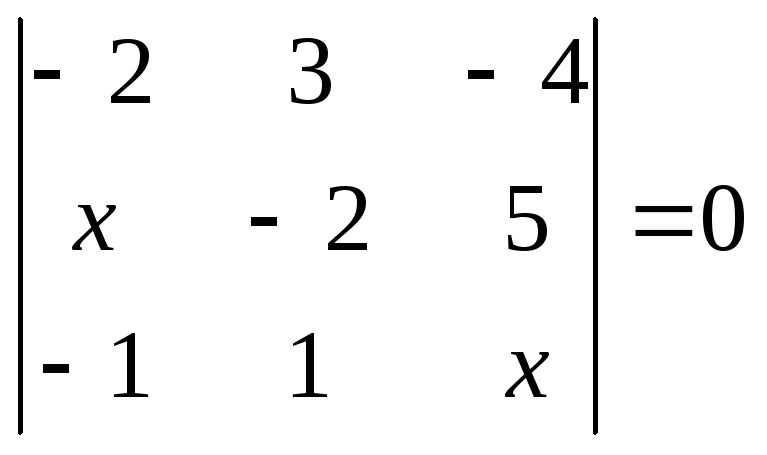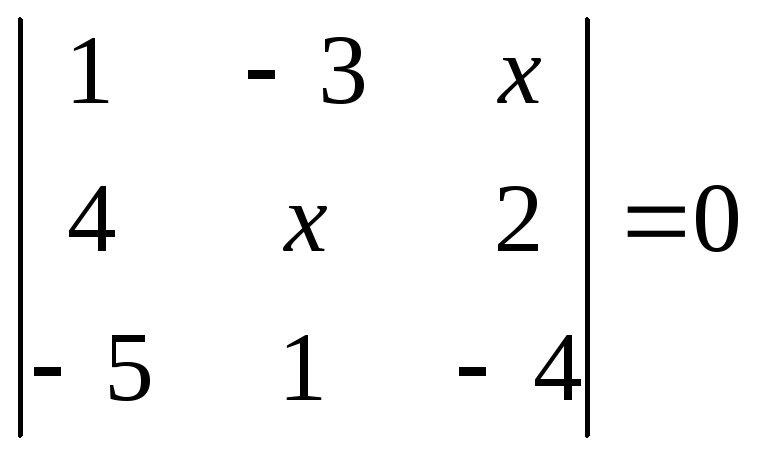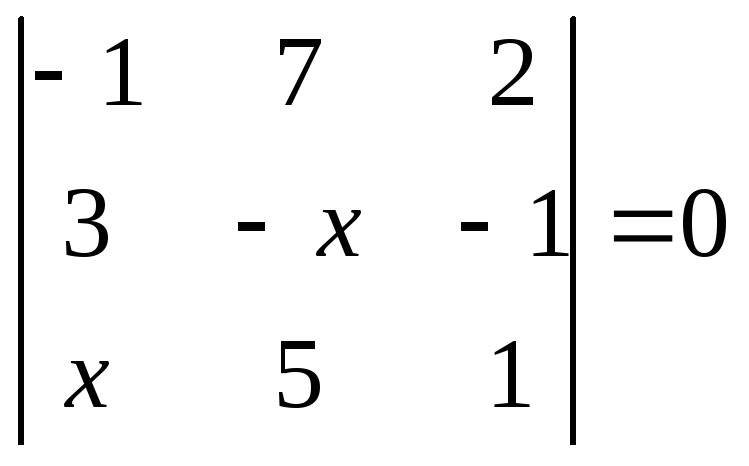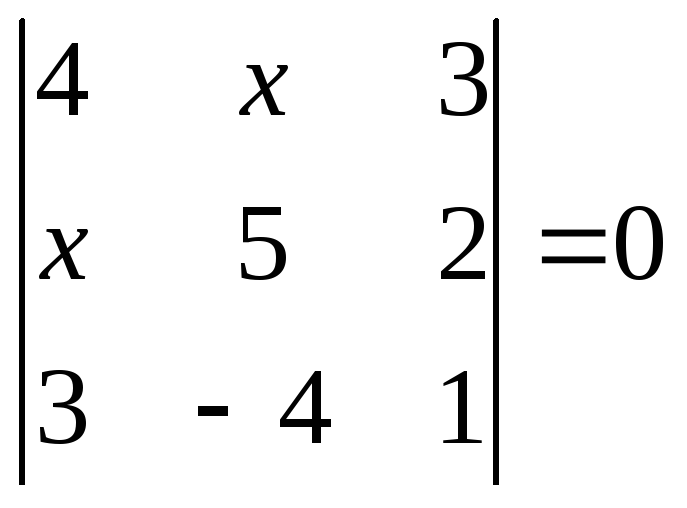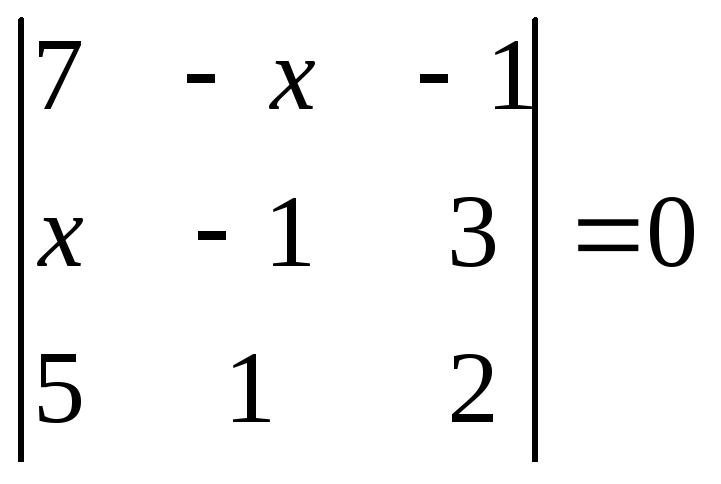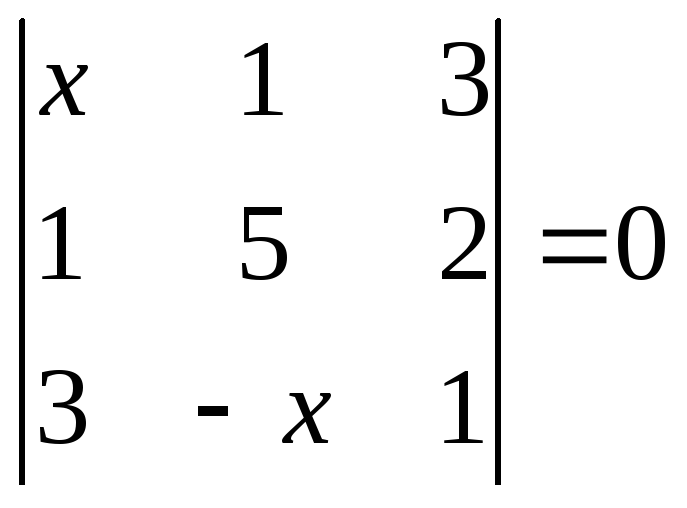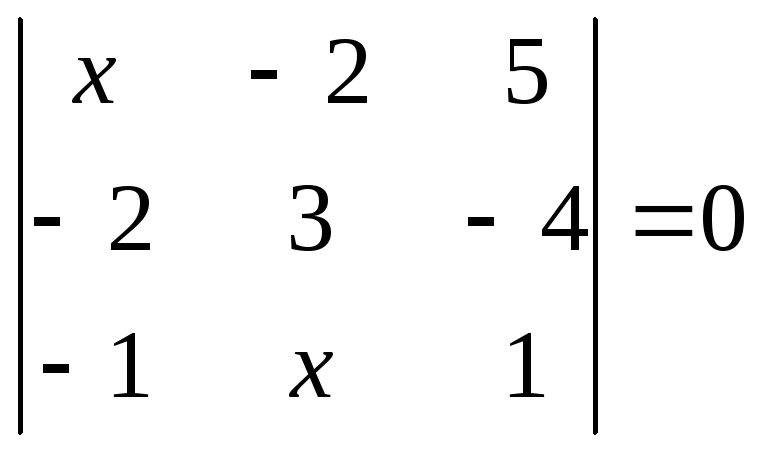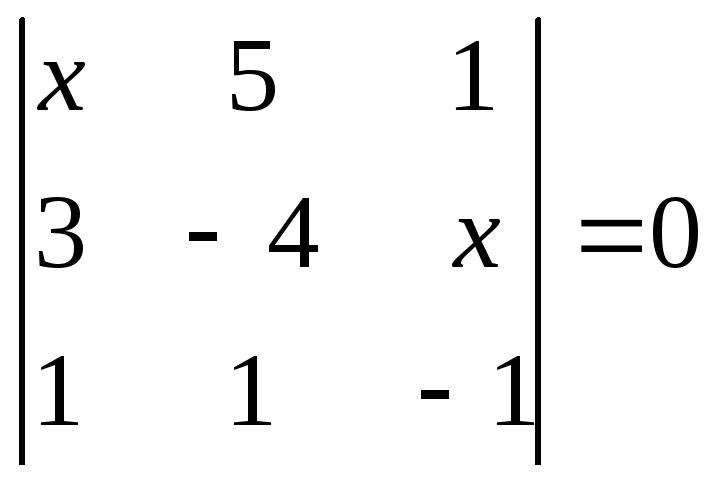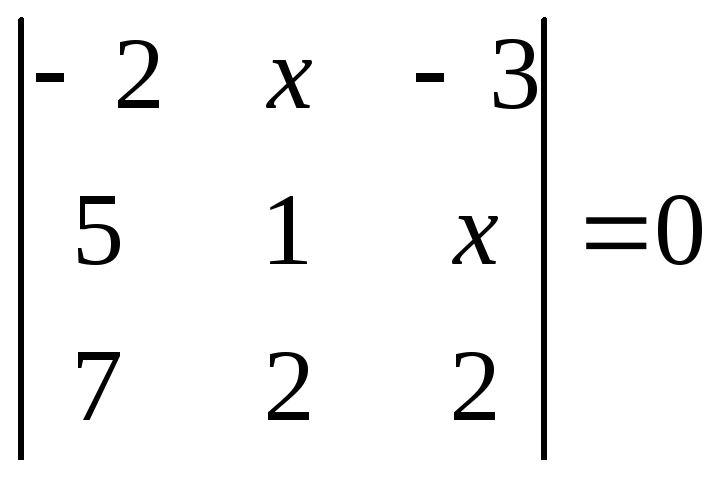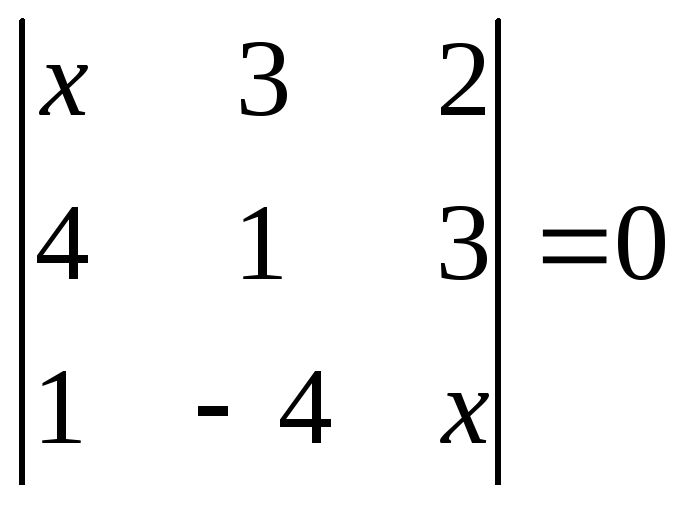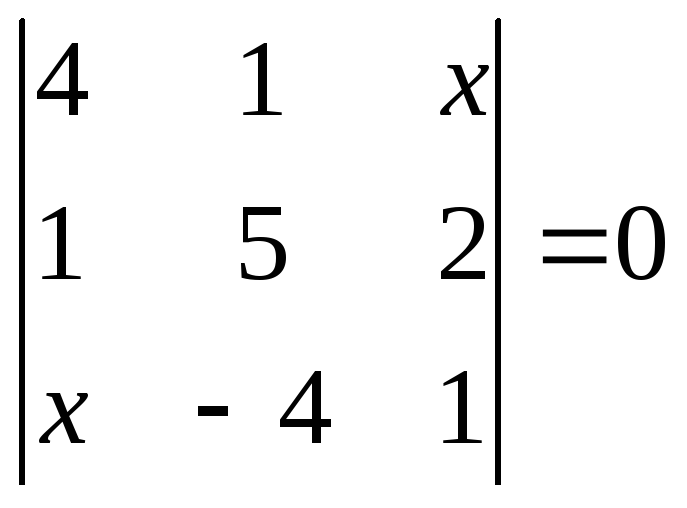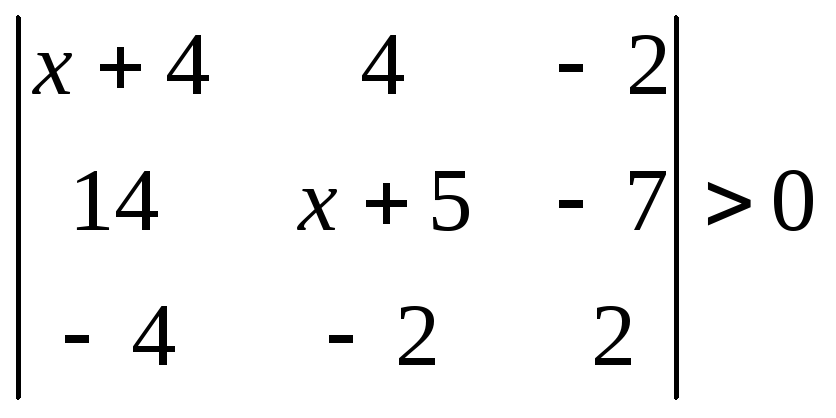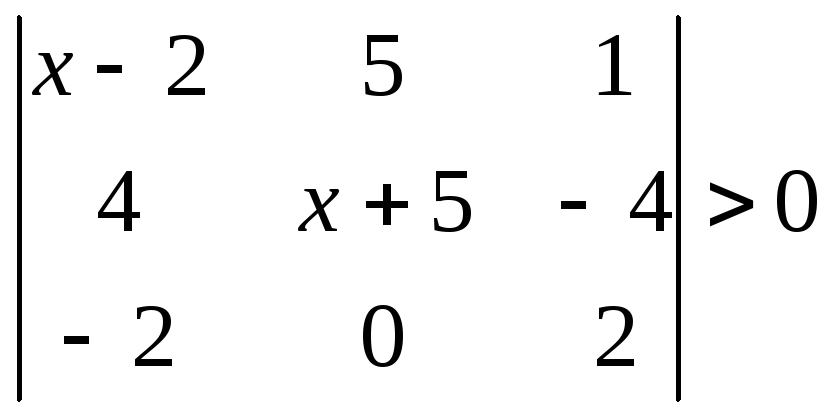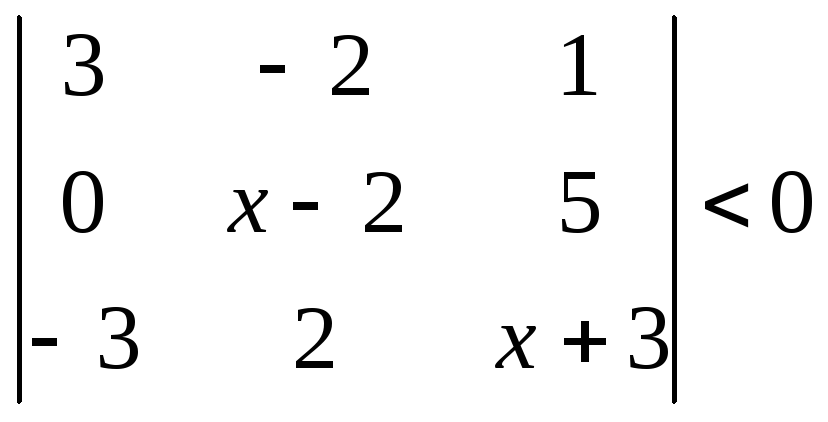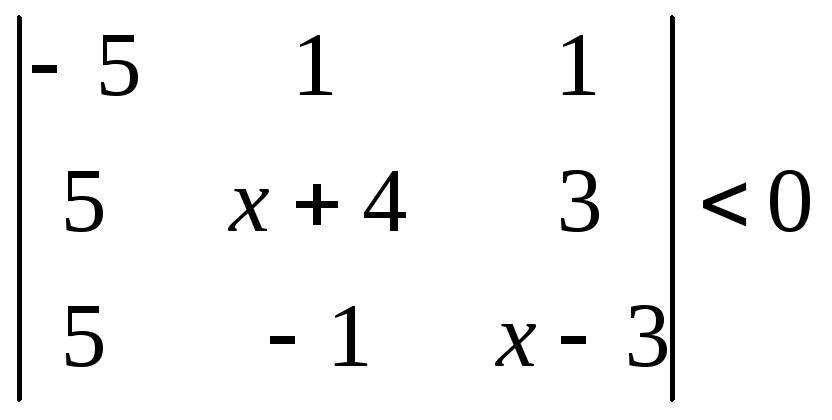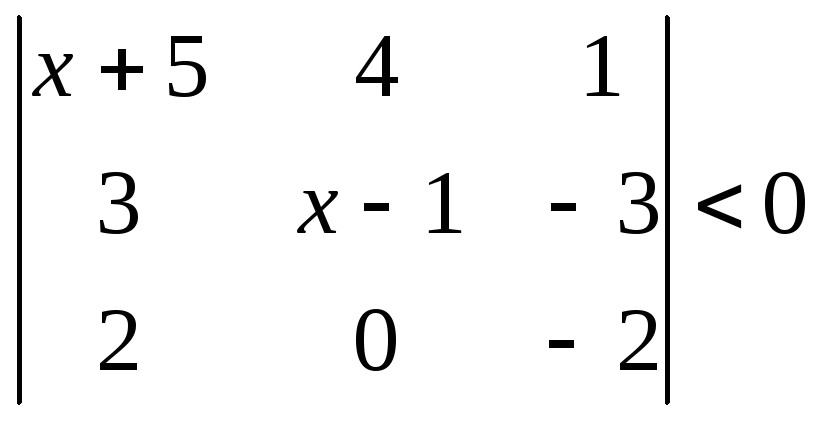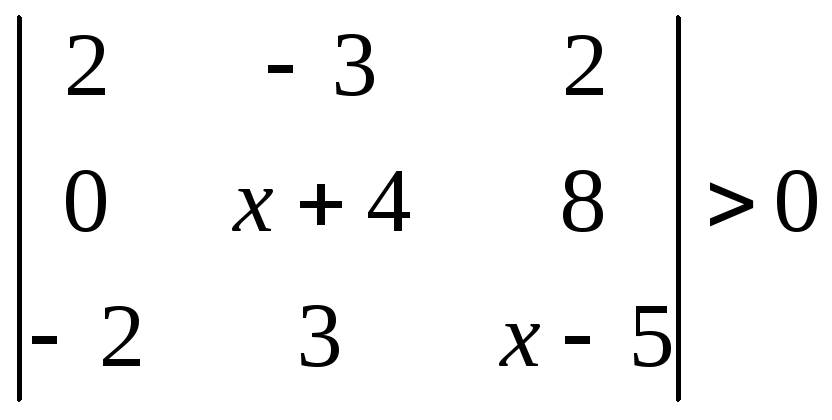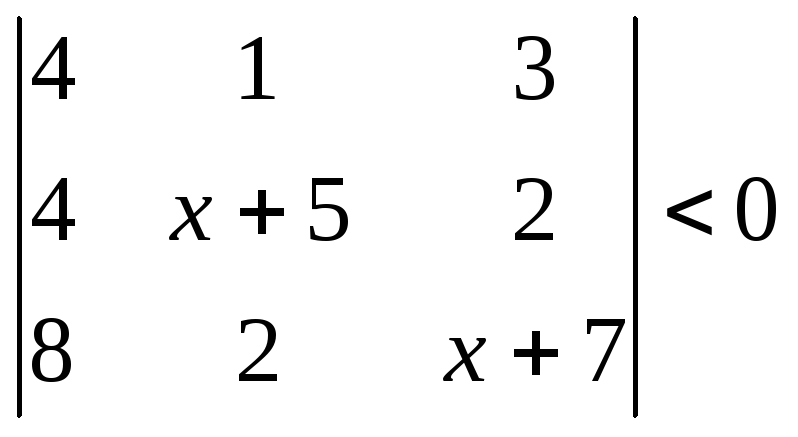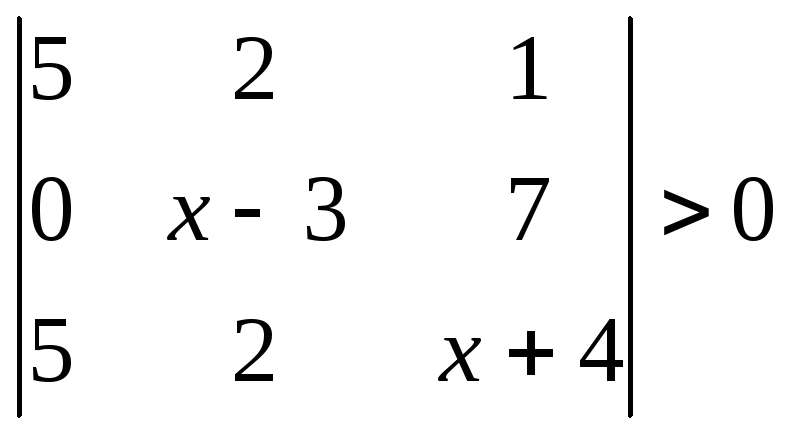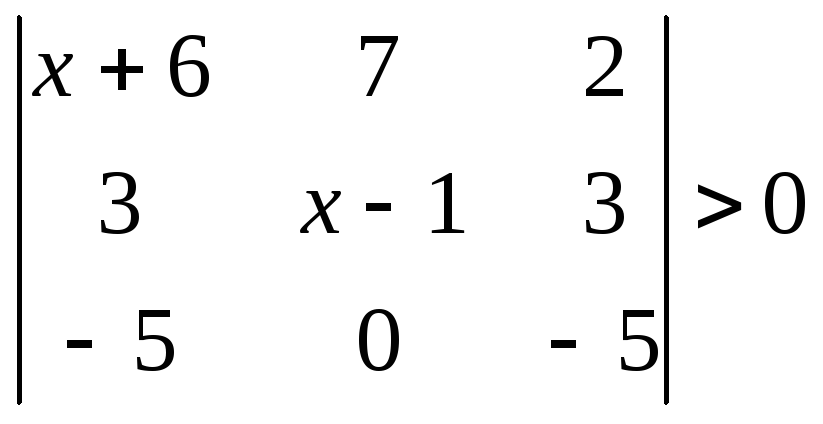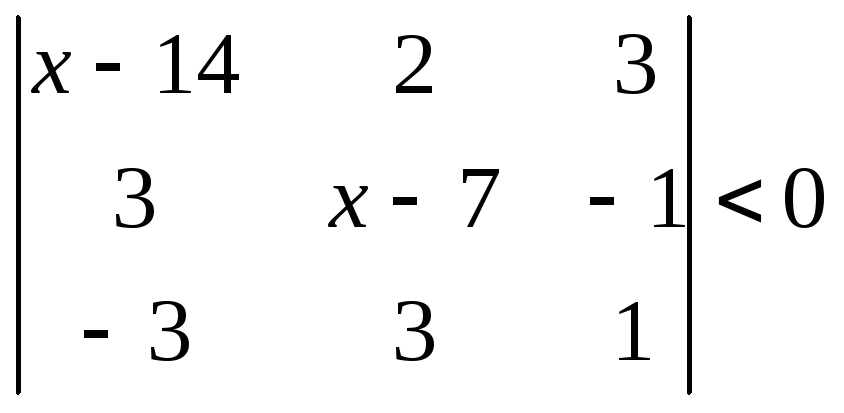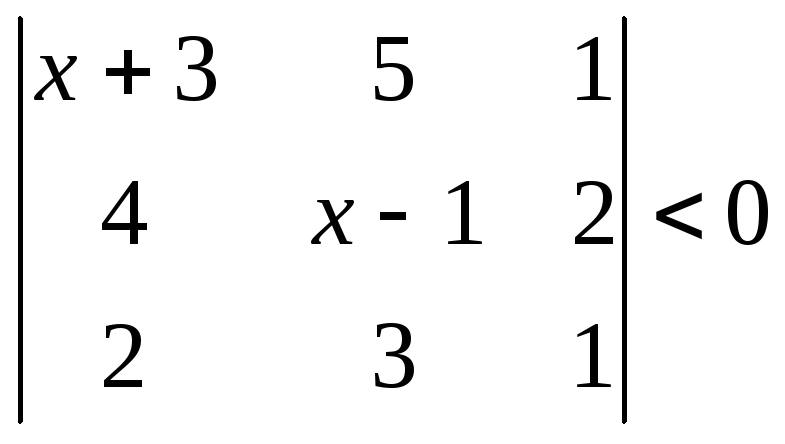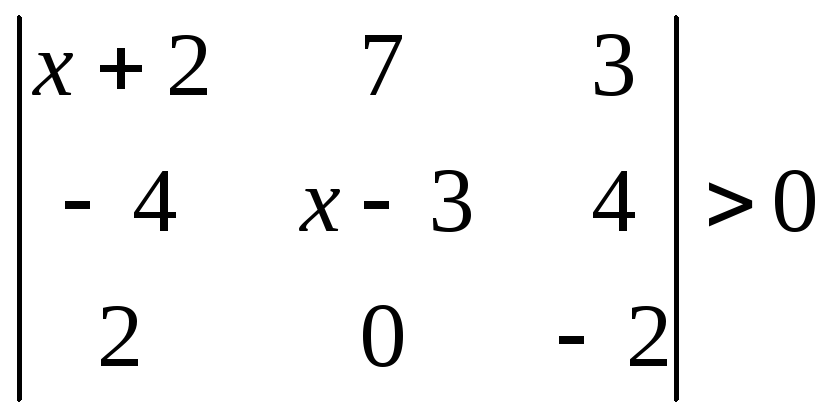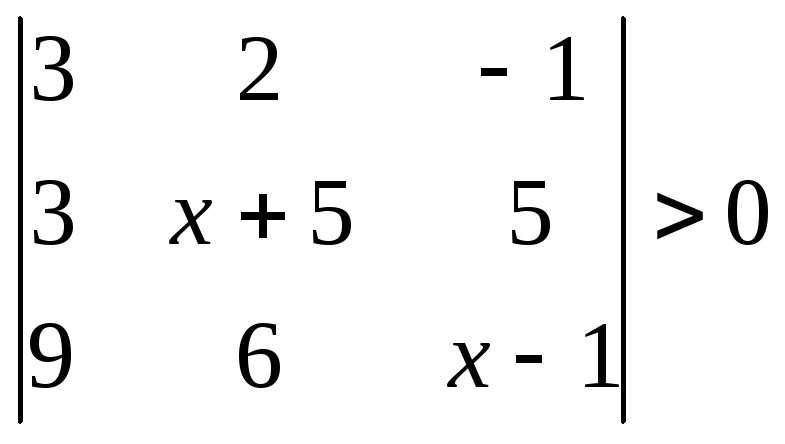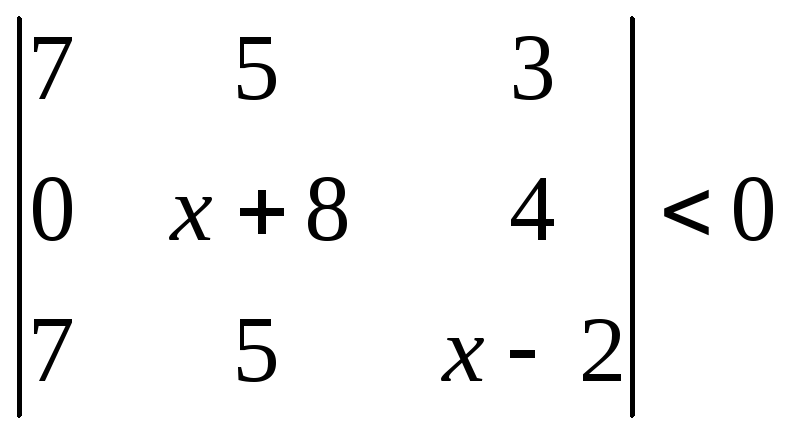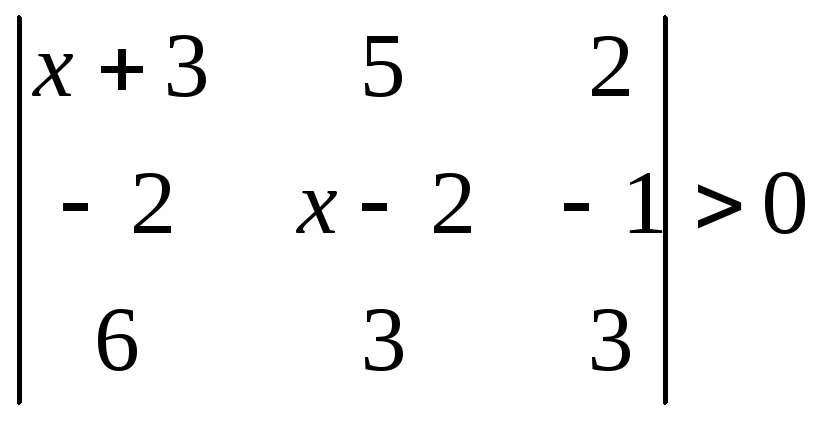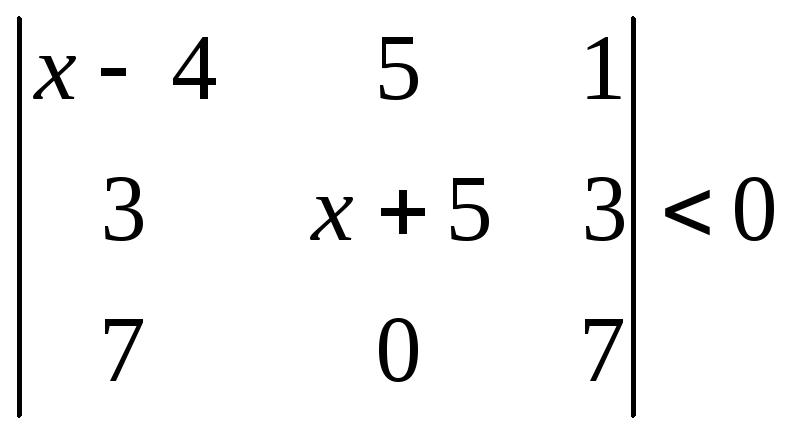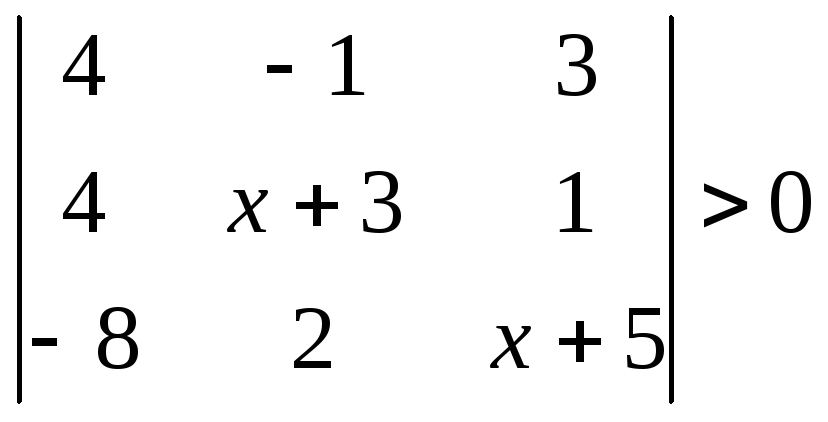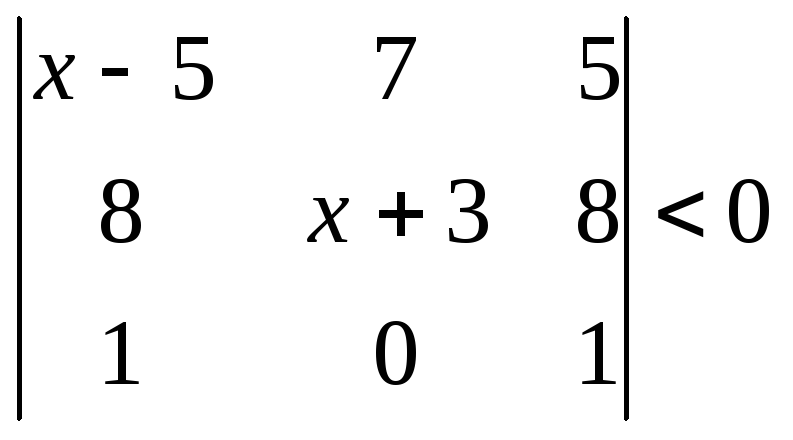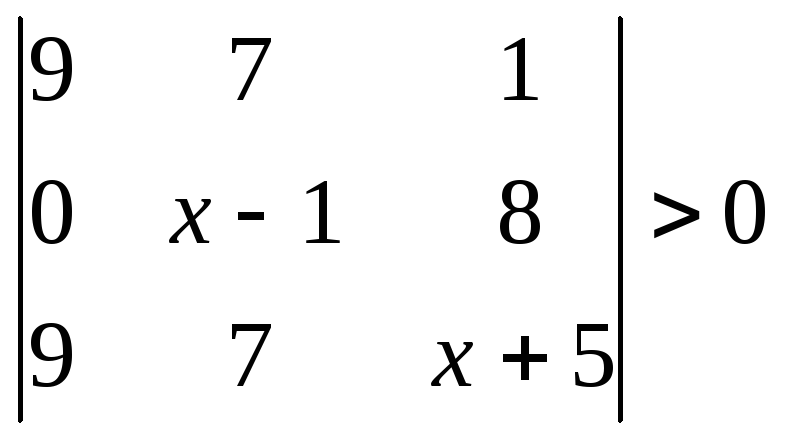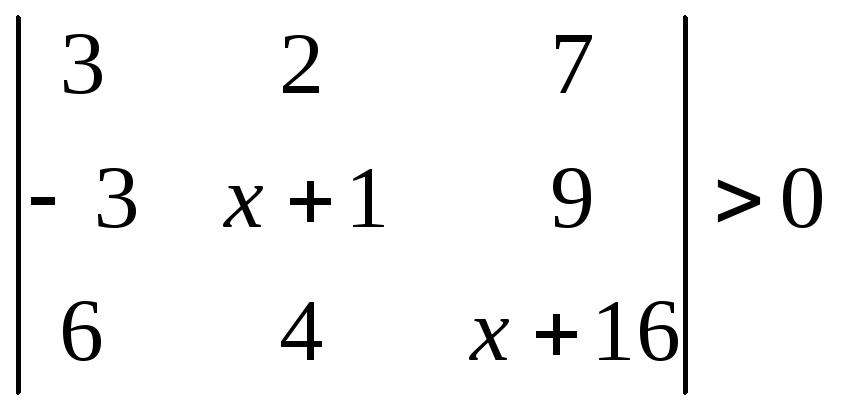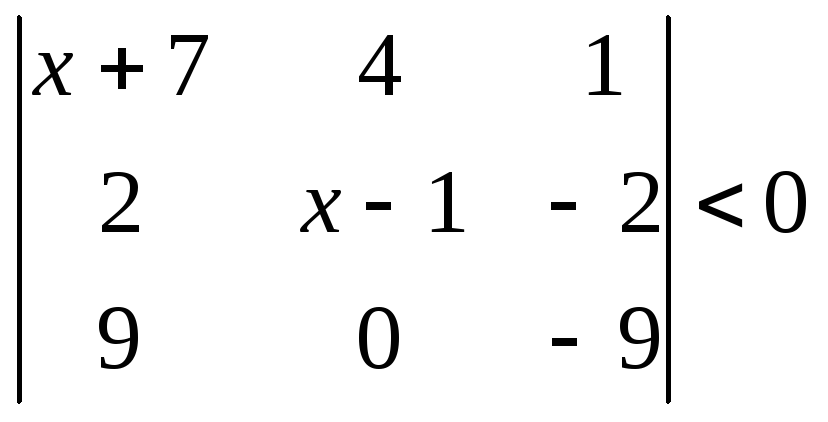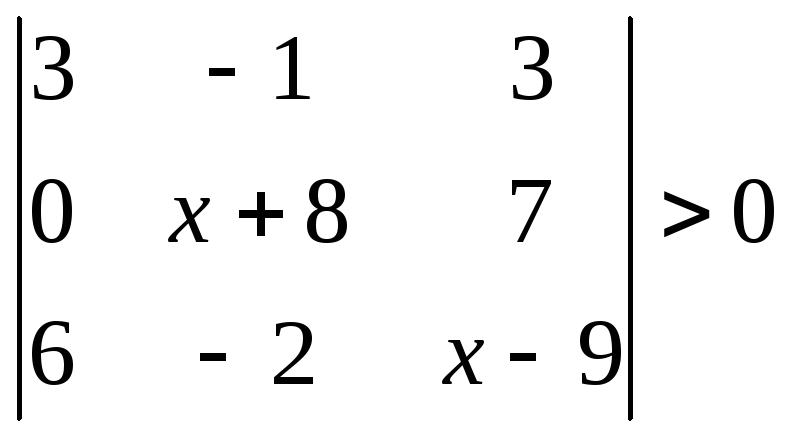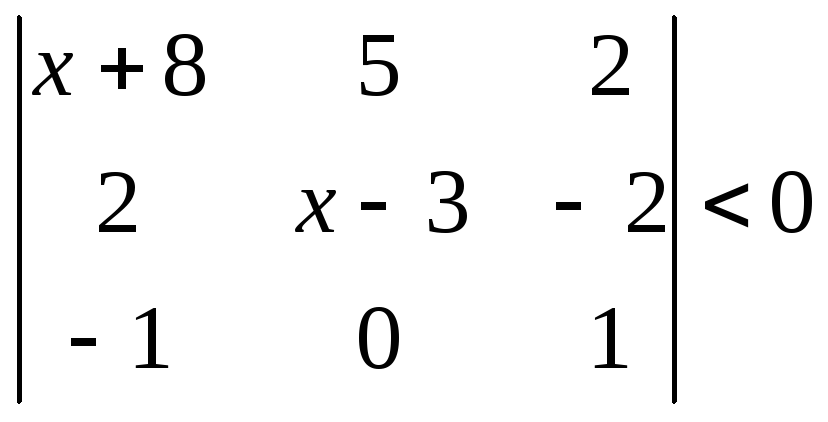- •Міністерство освіти і науки україни
- •1. Лінійна алгебра
- •1.1 Аудиторні завдання
- •1.2 Індивідуальні завдання
- •1.2.1 Розвязати рівняння
- •1.2.3. Обчислити визначник 4-го порядку.
- •1.2.4 Розвязати систему рівнянь :
- •1.2.6 Виконати дії над матрицями
- •1.2.8. Розвязати матричне рівняння.
- •2.Векторна алгебра
- •2.1 Аудиторні завдання
- •2.2 Індивідуальні завдання
- •2.2.2 Знайти модулі суми та різниці векторів і ,.
- •2.2.3. Вектор розкладено за базисомI, ,. Знайти розклад за цим базисом вектораd, протилежно напрямленого до вектора с, якщо відомий модуль вектора d.
- •2.2.4. Дано чотири вектори: . Якщо вектори утворюють базис, знайти розвинення вектораm за цим базисом.
- •2.2.6. Скалярний добуток векторів
- •2.2.9 Знайти роботу, яку виконує сила f , рухаючись прямолінійно із точки а в точку в.
- •2.2.11 Обчислити площу паралелограму, побудованого на векторах m та n і знайти скалярний добуток .
- •2.2.12 Дано вектори а та. Знайти координати векторного добутку.
- •2.2.13 Знайти момент сили p відносно точки с, якщо сила прикладена до точки а.
- •2.2.14 Дано координати вершин трикутника авс. Знайти ,, довжину висоти вd та внутрішній й зовнішній кут при вершині а.
- •2.2.15 Дано вектори а, с. Знайти їх мішаний добуток і зясувати, праву чи ліву трійку утворюють дані вектори.
- •2.2.16 Зясувати, чи знаходяться чотири точки, координати яких задані, на одній площині.
- •2.2.17 Обчислити обєм тетраедра з вершинами у точках а, в, с, d та його висоту, опущену з вершини d на грань авс.
- •3. Аналітична геометрія на площині
- •3.1 Аудиторні завдання
- •3.2. Індивідуальні завдання
- •3.2.1 Трикутник авс задано координатами його вершин. Зробити креслення і знайти:
- •3.2.2 Знайти рівняння прямих, , які проходять через т.M і розташовані паралельно та перпендикулярнодо відомої прямоїl. Рівняння прямої l записати у «відрізках» та побудувати її.
- •3.2.5 Перейшовши до полярних координат, побудувати криву, задану рівнянням у декартових координатах.
- •4. Пряма та площина у просторі
- •4.1 Аудиторні завдання
- •4.2 Індивідуальні завдання
- •Варіанти індивідуальних завдань
- •5.Поверхні другого порядку
- •6. Лінійні оператори
- •6.1 Аудиторні завдання
- •6.2 Індивідуальні завдання
- •Варіанти індивідуальних завдань
- •Література
Міністерство освіти і науки україни
Запорізький національний технічний університет
Індивідуальні завдання з вищої
математики
для студентів технічних спеціальностей
денної форми навчання
(1-й семестр)
1 частина
2010
Індивідуальні завдання з вищої математики для студентів технічних спеціальностей денної форми навчання (1-й семестр) 1 частина.
/ Укл.: Засовенко В.Г., Засовенко А.В., Килимник І.М., Паталаха Л.І., Полякова Т.Г., Попригіна Т.Ф. – Запоріжжя: ЗНТУ, 2010.- 82 с
Укладачі: Засовенко В.Г., к.ф.-м. наук, доцент
Засовенко А.В., к.т.н., ст.викл.,
Килимник І.М., к.т.н., доцент
Паталаха Л.І., асистент
Полякова Т.Г, асистент
Попригіна Т.Ф., ст.. викл.
Рецензент: Онуфрієнко В.М., д.ф.-м.наук., професор
Відповідальний за випуск: Килимник І.М., к.т.н., доцент
Комп'ютерна верстка : Давиденко С.І.
Затверджено на засіданні кафедри вищої математики ЗНТУ
Протокол № 3 від 17.10.10. р.
ЗмісТ
|
|
|
Стор. |
|
1. |
Лінійна алгебра. |
4 |
|
1.1 |
Аудиторні завдання |
4 |
|
1.2 |
Індивідуальні завдання |
8 |
|
2. |
Векторна алгебра |
25 |
|
2.1 |
Аудиторні завдання |
25 |
|
2.2 |
Індивідуальні завдання |
27 |
|
3. |
Аналітична геометрія на площині |
54 |
|
3.1 |
Аудиторні завдання |
54 |
|
3.2 |
Індивідуальні завдання |
56 |
|
4. |
Пряма та площина у просторі |
64 |
|
4.1 |
Аудиторні завдання |
64 |
|
4.2 |
Індивідуальні завдання |
65 |
|
5. |
Поверхні другого порядку |
66 |
|
5.1 |
Аудиторні завдання |
66 |
|
5.2 |
Індивідуальні завдання |
66 |
|
6. |
Лінійні оператори |
70 |
|
6.1 |
Аудиторнізавдання |
70 |
|
6.2 |
Індивідуальні завдання |
71 |
|
|
Література |
82 |
1. Лінійна алгебра
1.1 Аудиторні завдання
1.Розвязати рівняння та нерівності.
1)
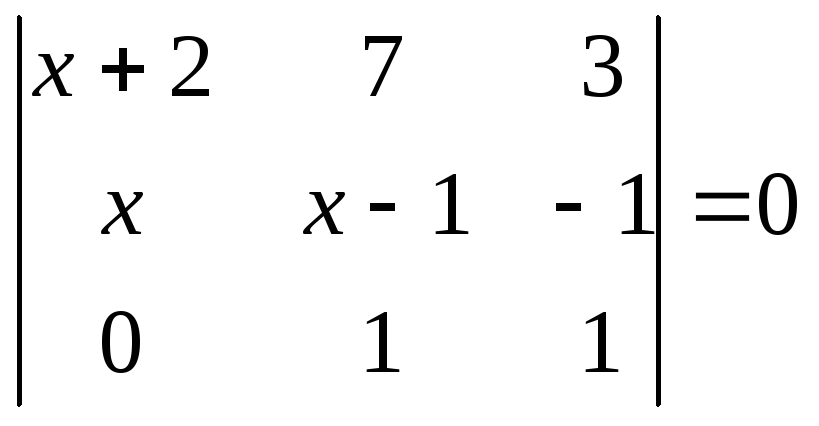 Відповідь:0
2.
Відповідь:0
2.
2)
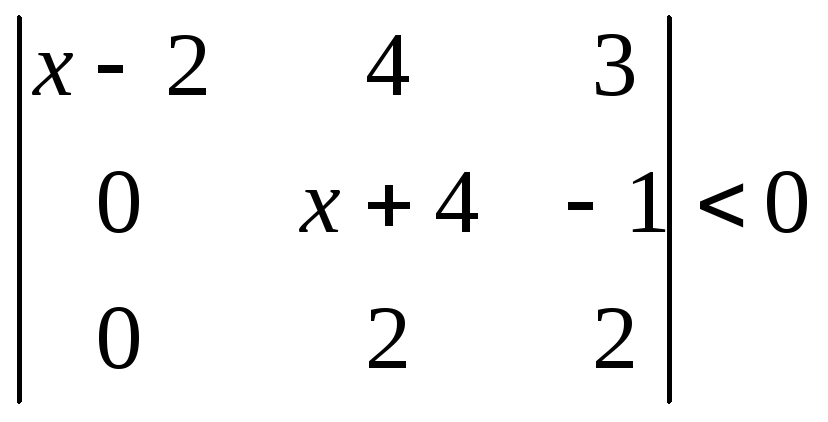 Відповідь:х(-5
2).
Відповідь:х(-5
2).
3)
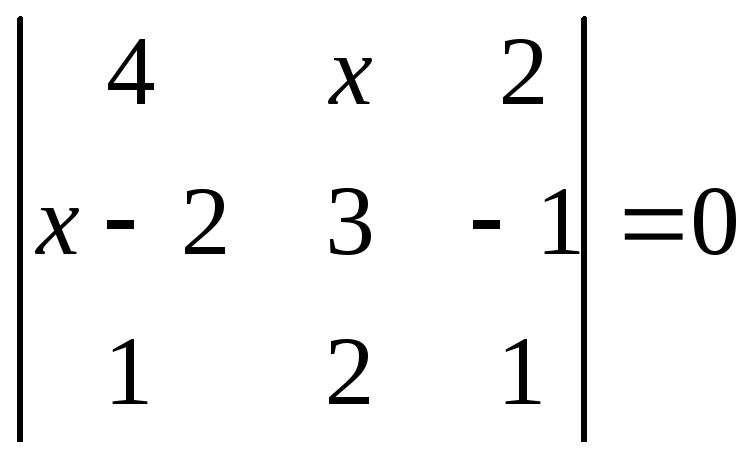 Відповідь:6
-1.
Відповідь:6
-1.
4)
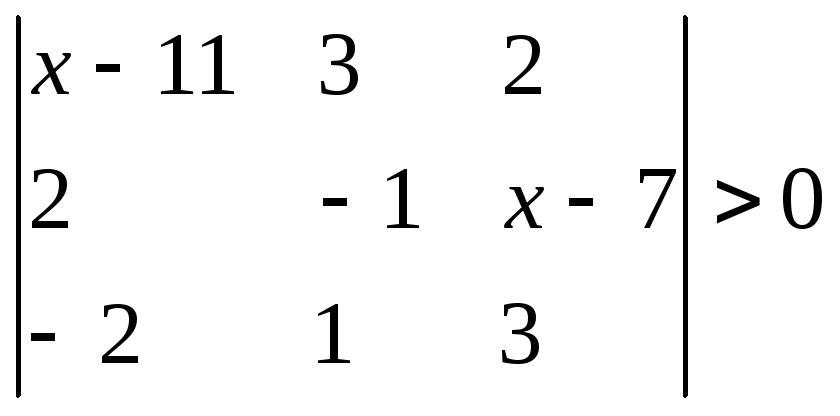 Відповідь:х(4
5).
Відповідь:х(4
5).
2.Обчислити визначники 4-го порядку:
а) розклавши по елементам 1-го рядка
б)використавши властивості визначників.
1)
 Відповідь:
30.
Відповідь:
30.
2)
 Відповідь:
-20
Відповідь:
-20
3)
 Відповідь:
0.
Відповідь:
0.
4)
 Відповідь:
48.
Відповідь:
48.
3. Розвязати систему лінійних рівнянь а) за правилом Крамераб) матричним способомв) методом Гауса.
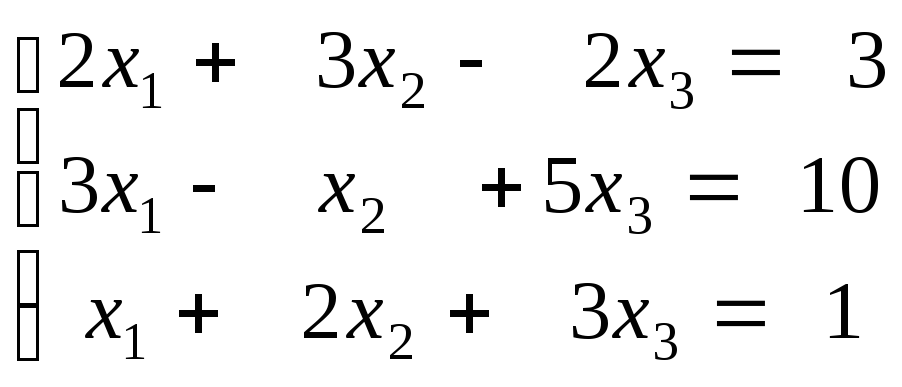 Відповідь:
(3-10)
Відповідь:
(3-10)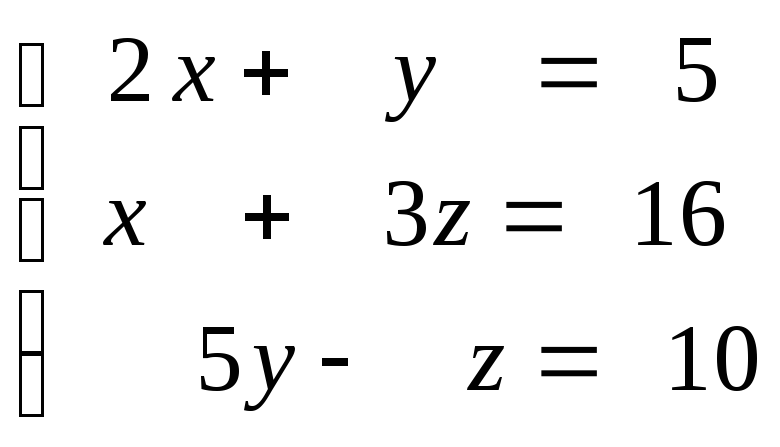 Відповідь:
(135)
Відповідь:
(135)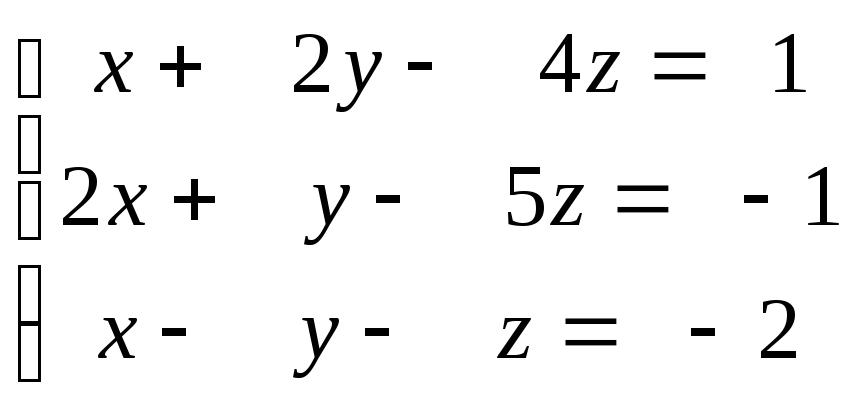 Відповідь:
Відповідь:
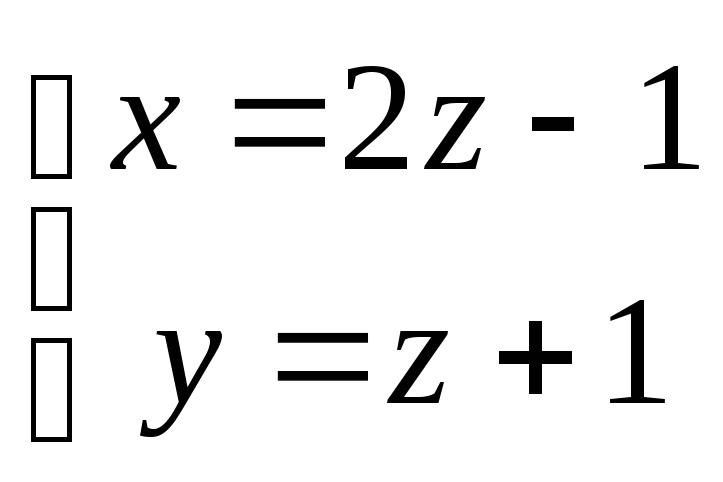
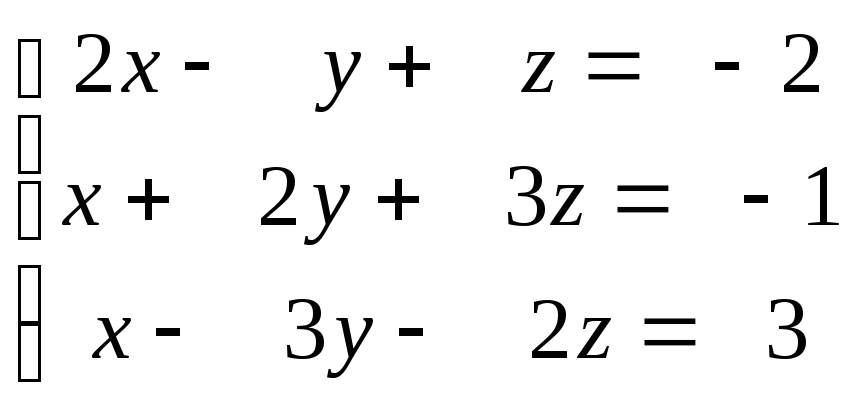 Відповідь:
.
Відповідь:
.
4.Розвязати однорідні системи лінійних рівнянь
1)
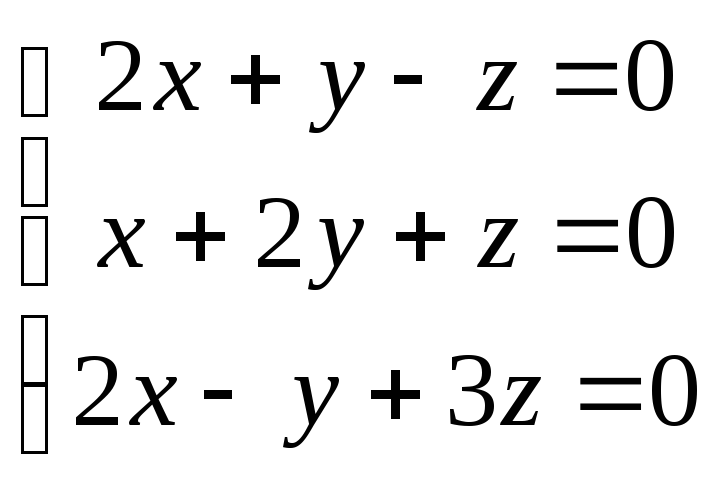 Відповідь:(000)
Відповідь:(000)
2)
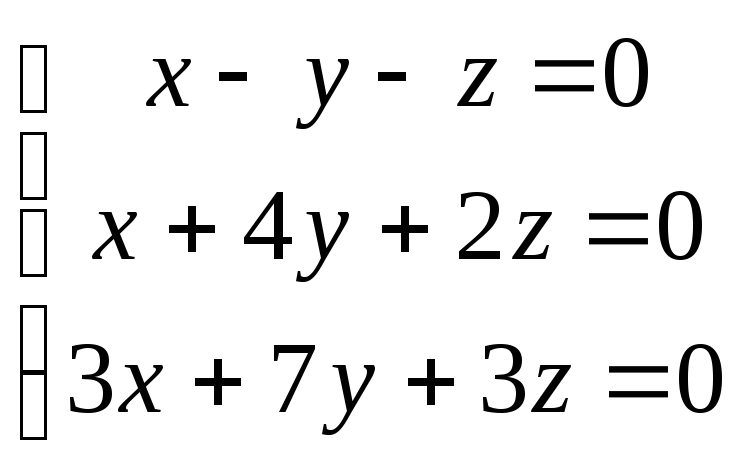 Відповідь:
Відповідь: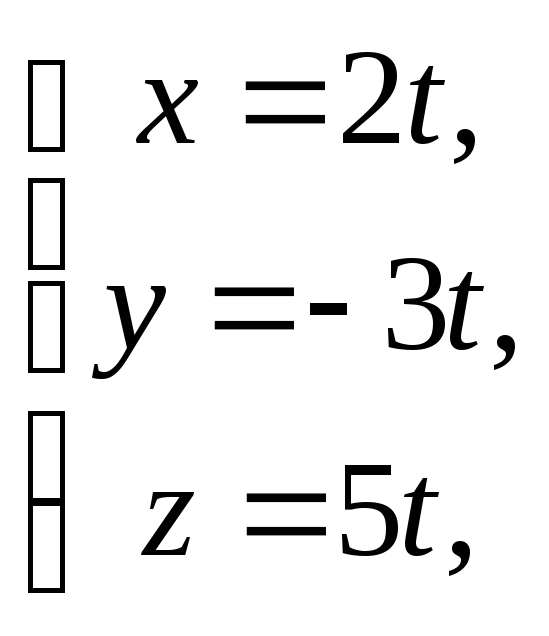 де
де![]()
3)
 Відповідь:
Відповідь: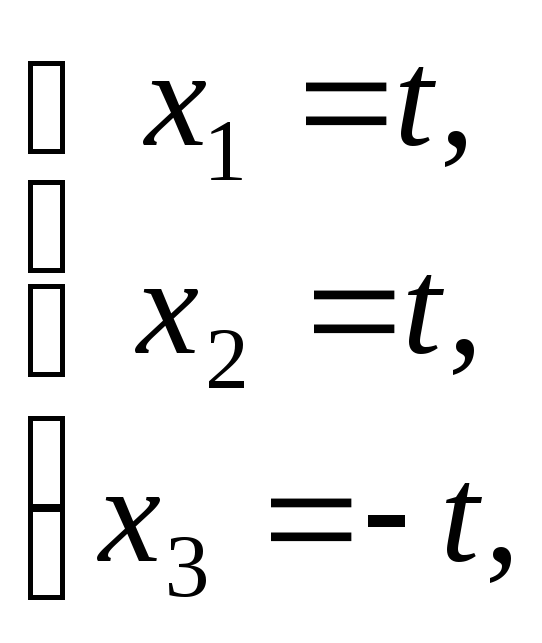 де
де![]()
5. Виконати дії над матрицями:
1)
![]() Відповідь:
Відповідь:![]()
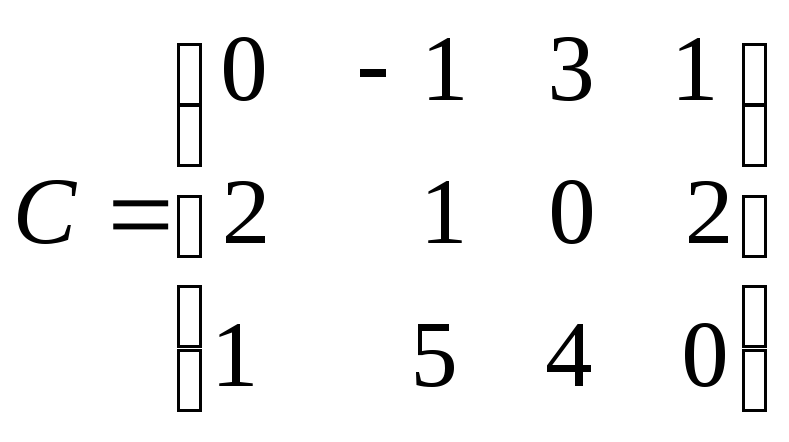
2)
![]() Відповідь:
Відповідь:
![]()
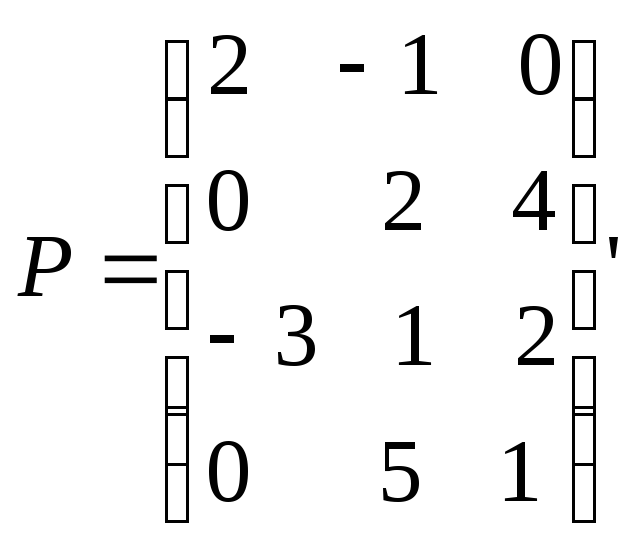
![]()
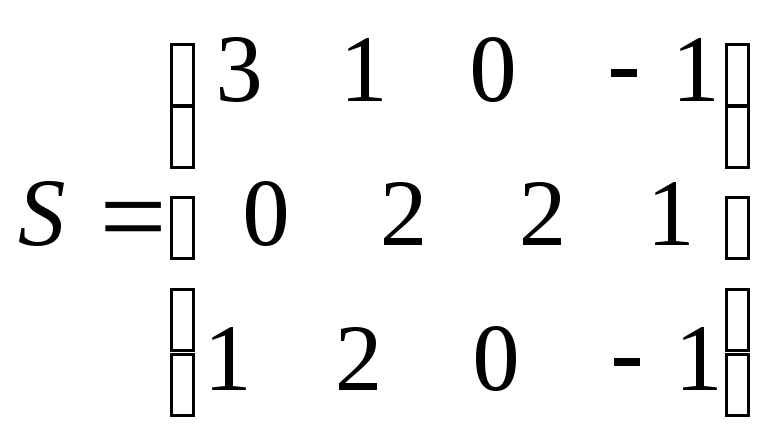
6. Знайти
значення многочлена
![]() ,
деА
– матриця, якщо
,
деА
– матриця, якщо
![]() .
.
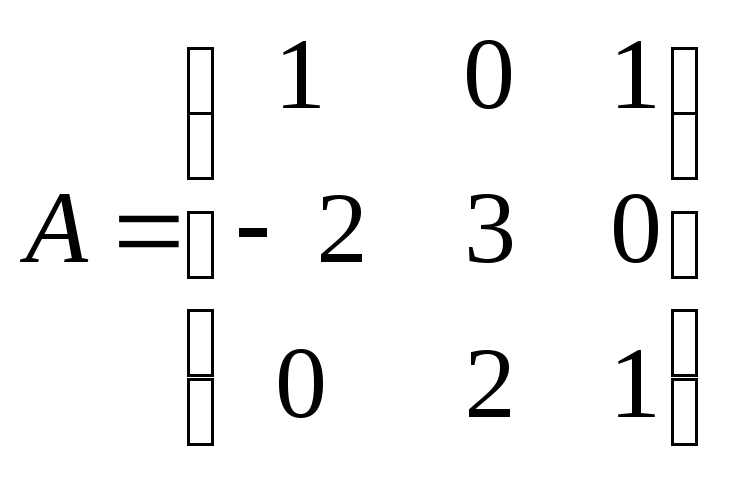 Відповідь:
Відповідь:
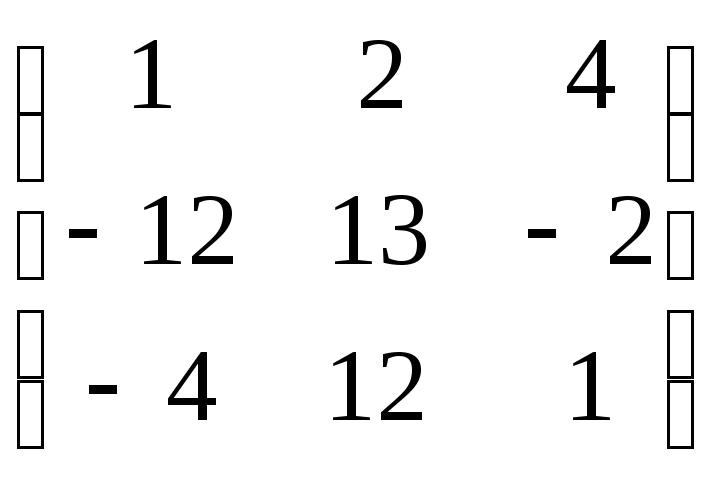 .
.
7. Розвязати матричні рівняння:
1)
![]() Відповідь:
Відповідь:![]()
2)
![]() Відповідь:
Відповідь:![]()
8. Дослідити систему лінійних рівнянь за теоремою Кронекера-Капеллі, знайти всі розвязки системи:
1)
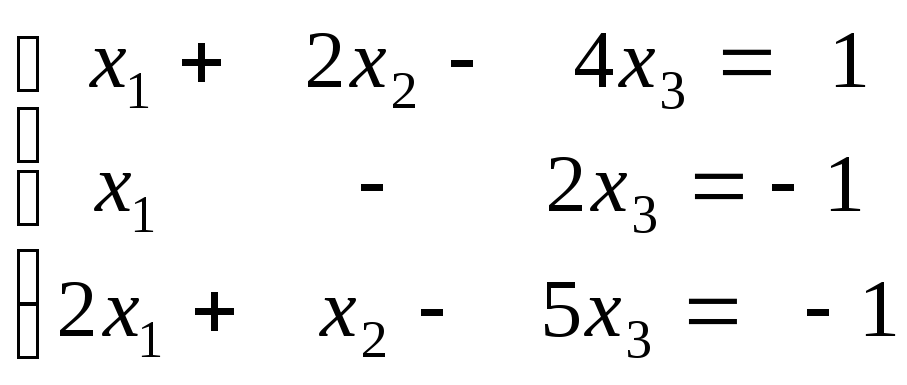 Відповідь:
Відповідь: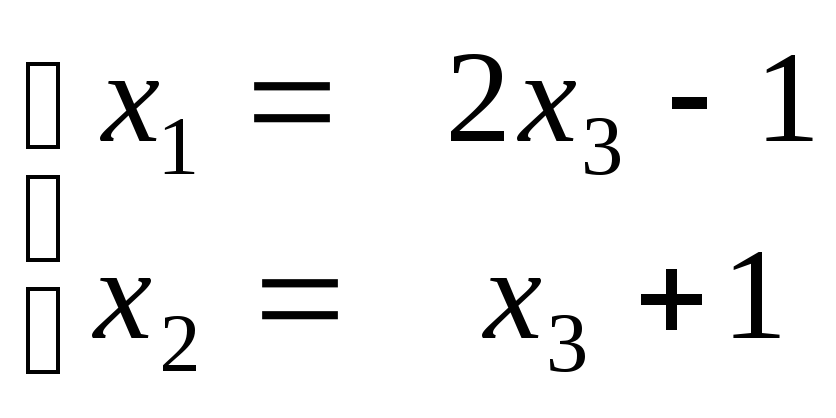
2)
 Відповідь:
Відповідь: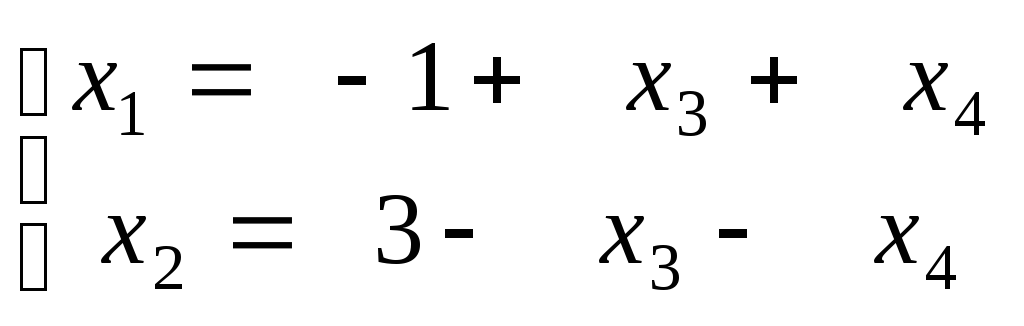
3)
 Відповідь:
Відповідь: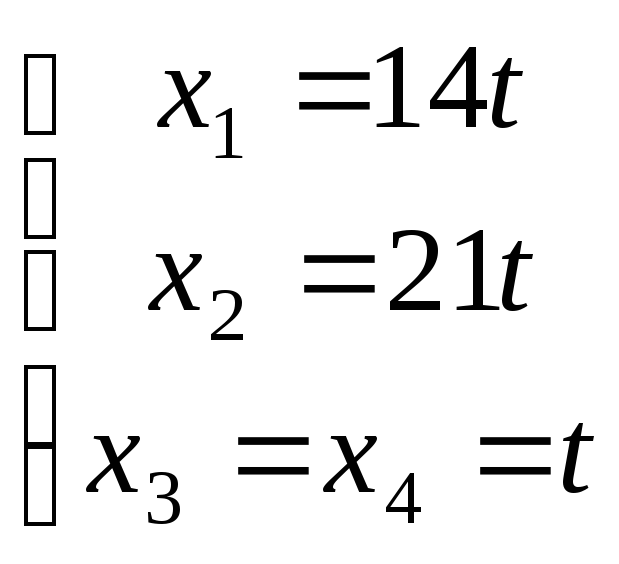
4)
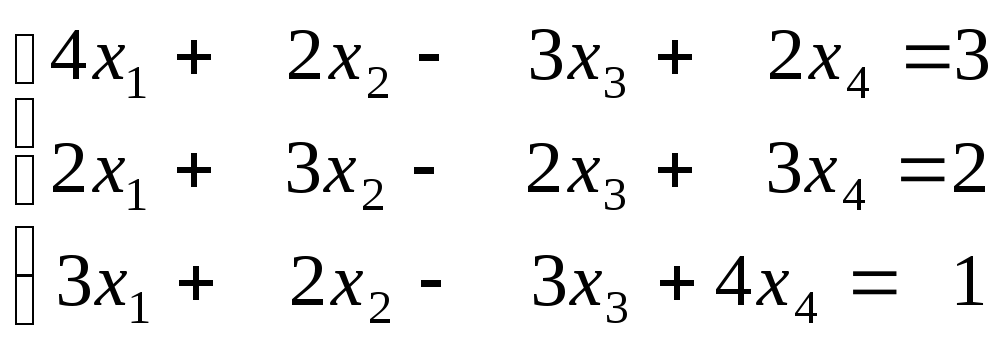 Відповідь:
Відповідь: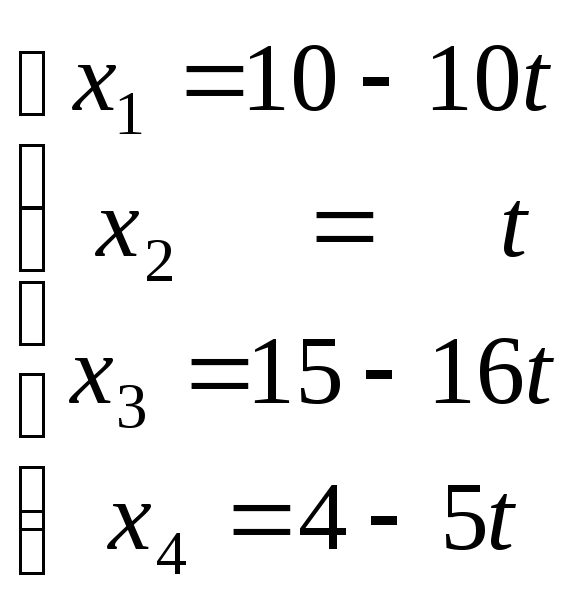
5)
 Відповідь:
Відповідь: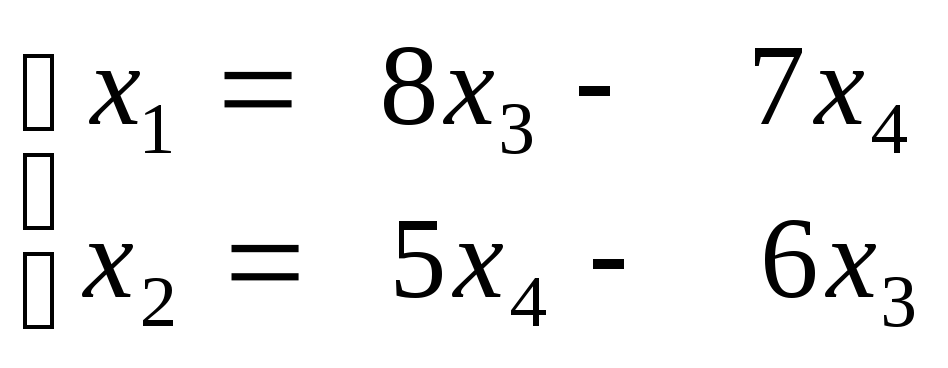
1.2 Індивідуальні завдання
1.2.1 Розвязати рівняння
|
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10. |
|
11. |
|
12. |
|
|
13. |
|
14. |
|
15. |
|
|
16. |
|
17. |
|
18. |
|
|
19. |
|
20. |
|
21. |
|
|
22. |
|
23. |
|
24. |
|
|
25. |
|
26. |
|
27. |
|
|
28. |
|
29. |
|
30. |
|
1.2.2 Розвязати нерівність.
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
26. |
|
|
27. |
|
28. |
|
|
29. |
|
30. |
|