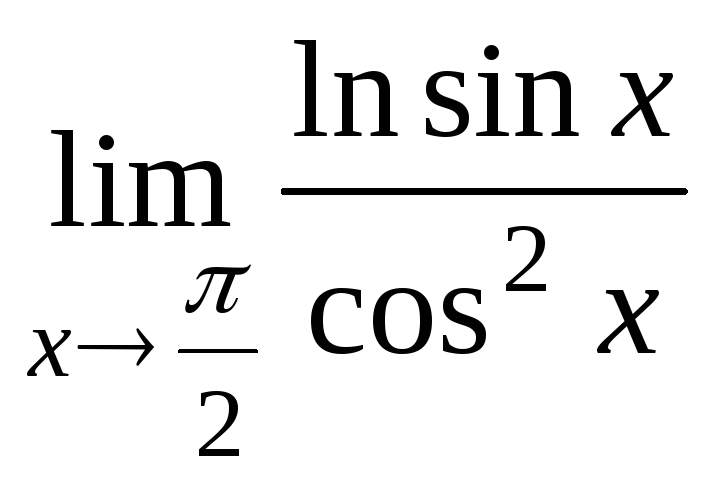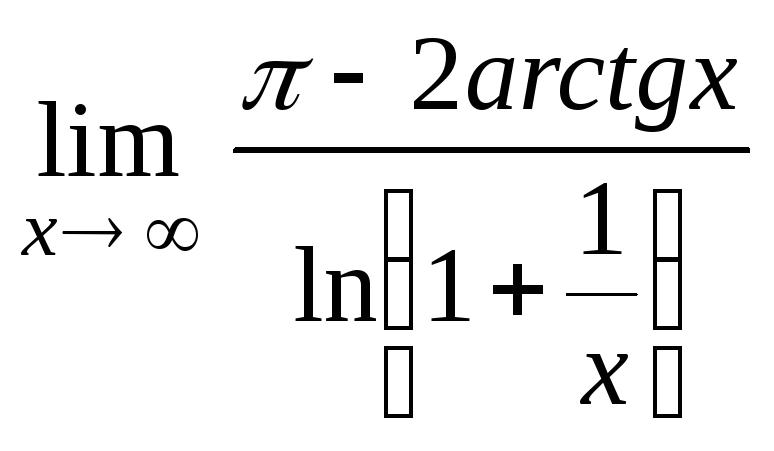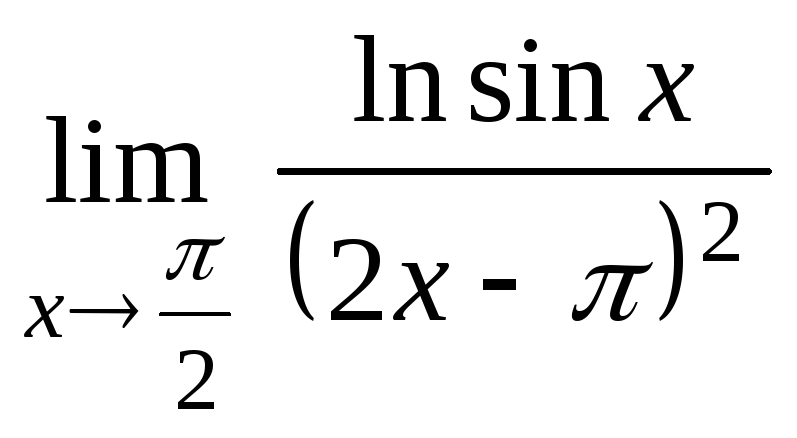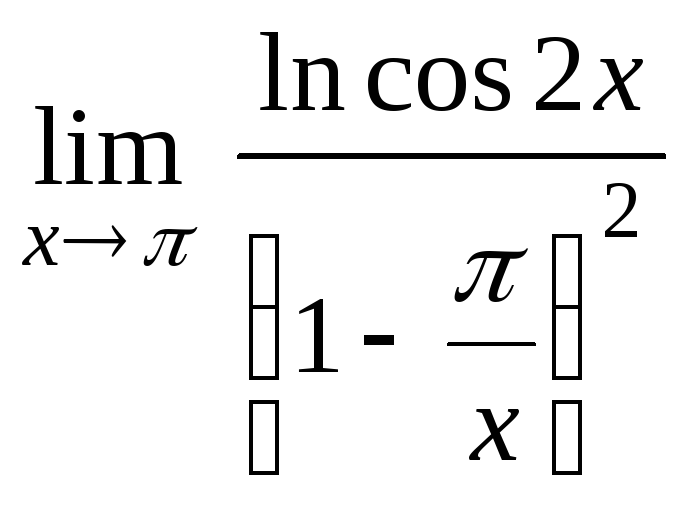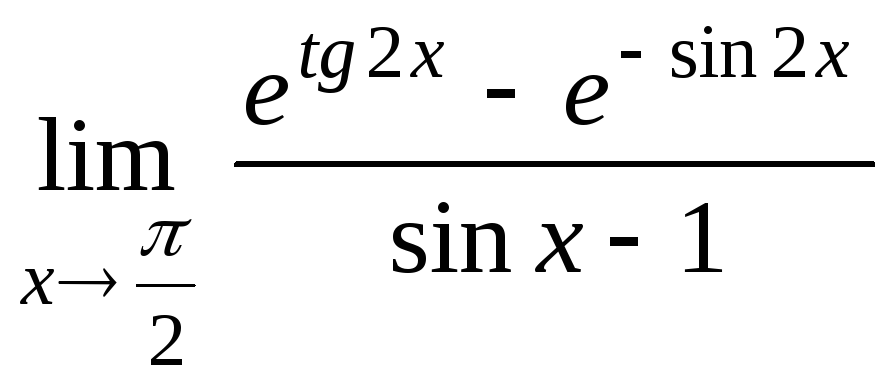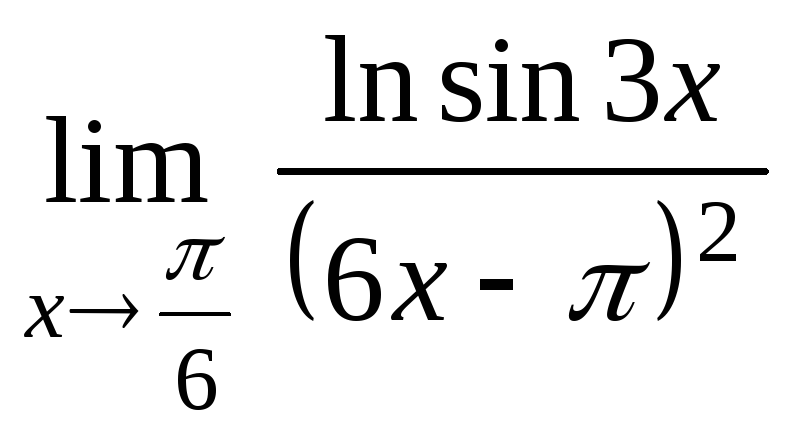- •Міністерство освіти і науки україни
- •1.Границя функції
- •1.1 Аудиторні завдання
- •1.2 Індивідуальні завдання
- •1.2.5 Знайти границі
- •1.2.6 Знайти границі
- •1.2.8 Знайти границі
- •1.2.10 Знайти границі
- •1.2.11 Знайти границі
- •1.2.12 Знайти границі
- •1.2.13 Знайти границі
- •1.2.14 Знайти границі
- •1.2.15 Знайти границі
- •1.2.16 Знайти границі
- •1.2.17 Знайти границі
- •1.2.18 Знайти границі
- •2.Неперервність функції
- •2.1 Аудиторні завдання
- •2.2 Індивідуальні завдання.
- •2.2.1 Знайти область визначення функції
- •2.2.2 Дослідити функцію на неперервність. Побудувати схематичний графік функції.
- •2.2.3 Дослідити функцію на неперервність. Побудувати схематичний графік функції.
- •2.2.4 Дослідити функцію на неперервність. Побудувати схематичний графік функції.
- •2.2.5 Дослідити функцію на неперервність. Побудувати схематичний графік функції
- •3. Диференціальне числення функції однієї змінної
- •3.1. Аудиторні завдання
- •3.2 Індивідуальні завдання
- •3.2.1 Знайти похідну функції, використовуючи визначення похідної.
- •3.2.2 Знайти похідну функції, використовуючи таблицю похідних та правила диференціювання
- •3.2.3 Знайти похідні функцій, використовуючи логарифмічне диференціювання
- •3.2.4.Знайти першу і другу похідну функції, заданої неявно
- •3.2.5 Знайти функції, заданої параметрично
- •3.2.6 Знайти другу похідну функції
- •3.2.7 Знайти границі, застосовуючи правило Лопіталя
- •3.2.8 Довести, що задана функція є розвязком рівняння
- •3.2.9 Знайти похідну n-го порядку
- •3.2.10 Знайти найбільше та найменше значення даних функцій у заданих інтервалах
- •3.2.11 Дослідити функцію на екстремум за допомогою першої похідної. Знайти інтервали монотонності функції
- •3.2.12 Дослідити функцію на перегин. Знайти інтервали опуклості та угнутості графіка заданої функції
- •3.2.13 Знайти асимптоти кривих
- •3.2.14 Дослідити функцію та побудувати її графік
- •4.1 Аудиторні завдання
- •4.2 Індивідуальні завдання
- •4.2.8 Знайти екстремуми функції
- •Література
3.2.7 Знайти границі, застосовуючи правило Лопіталя
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
26. |
|
|
27. |
|
28. |
|
|
29. |
|
30. |
|
3.2.8 Довести, що задана функція є розвязком рівняння
|
1. |
|
|
|
2. |
|
|
|
3. |
|
|
|
4. |
|
|
|
5. |
|
|
|
6. |
|
|
|
7. |
|
|
|
8. |
|
|
|
9. |
|
|
|
10. |
|
|
|
11. |
|
|
|
12. |
|
|
|
13. |
|
|
|
14. |
|
|
|
15. |
|
|
|
16. |
|
|
|
17. |
|
|
|
18. |
|
|
|
19. |
|
|
|
20. |
|
|
|
21. |
|
|
|
22. |
|
|
|
23. |
|
|
|
24. |
|
|
|
25. |
|
|
|
26. |
|
|
|
27. |
|
|
|
28. |
|
|
|
29. |
|
|
|
30. |
|
|
3.2.9 Знайти похідну n-го порядку
|
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10 |
|
11 |
|
12. |
|
|
13. |
|
14. |
|
15. |
|
|
16 |
|
17 |
|
18. |
|
|
19 |
|
20 |
|
21. |
|
|
22 |
|
23 |
|
24. |
|
|
25 |
|
26 |
|
27. |
|
|
28 |
|
29 |
|
30. |
|
3.2.10 Знайти найбільше та найменше значення даних функцій у заданих інтервалах
|
1. |
|
- 4; 0 |
|
2. |
|
1; 3 |
|
3. |
|
-1; 4 |
|
4. |
|
-7; 2 |
|
5. |
|
-1; 2 |
|
6. |
|
-3; -1 |
|
7. |
|
-2; 1 |
|
8. |
|
-1; 3 |
|
9. |
|
-2; 1 |
|
10. |
|
-1; 4 |
|
11. |
|
-2; 1 |
|
12. |
|
0; /2 |
|
13. |
|
-1; 2 |
|
14. |
|
0; 3 |
|
15. |
|
-5;-1 |
|
16. |
|
0; |
|
17. |
|
-3;3 |
|
18. |
|
- |
|
19. |
|
0; |
|
20. |
|
1;3 |
|
21. |
|
- |
|
22. |
|
0;2 |
|
23. |
|
-1;0 |
|
24. |
|
-1;3 |
|
25. |
y= |
0;5 |
|
26. |
|
-3;3 |
|
27. |
|
[ |
|
28. |
|
-6;8 |
|
29. |
|
- |
|
30. |
|
0; |
3.2.11 Дослідити функцію на екстремум за допомогою першої похідної. Знайти інтервали монотонності функції
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
26. |
|
|
27. |
|
28. |
|
|
29. |
|
30. |
|