5. Получение полных наборов графов

6. Поиск максимальной клики и вычисление плотности графа

Кликой называют полный подграф, не являющийся частью другого полного подграфа. Количество вершин наибольшей (по числу вершин) клики в данном графе называют его плотностью.

Доказано, что задача определения плотности графа является NP-полной задачей. Эта задача является ключом к решению многих трудновычислимых задач. Например, задача установления изоморфности двух графов сводится к определению плотности графа, являющегося их модульным произведением.

int D;

void dens(int L, graf g)

{ if (L==0) D=1;

if (nrib(g)==0) { if (L+1>D) D=L+1; return; }

for (int i=0; i<g.n; i++) dens(L+1, neibgraf(g,i));

}

Здесь

D - глобальная переменная, значением которой является текущая нижняя оценка искомой плотности в процессе вычислений и сама плотность после их завершения;

L - текущий уровень NB-дерева;

graf - тип, соответствующий принятому представлению графа;

n или g.n - число вершин графа;

nrib(g) - функция, возвращающая число ребер графа;

neibgraf(g,i) - функция, возвращающая подграф ближайшего окружения i-той вер-шины в графе g.

Вызов функции вида

dens(0,G);

приведет к установке глобальной переменной D в значение, равное плотности графа G. Однако в таком простейшем виде представленный выше алгоритм малоэффективен, так как число узлов NB-дерева очень быстро растет с ростом числа вершин исходного графа Из (1) следует, что число узлов растет быстрее, чем n!. Рассмотрим некоторые приемы, которые могут существенно улучшить алгоритм.

7. Задача коммивояжера

(По материалам [3])

Существует великое множество проблем, связанных с поиском оптимального решения, которые можно сформулировать как задачу коммивояжера (ЗК) в терминах теории графов. Исследованию природы ЗК посвящено большое число публикуемых работ.

Известно, что ЗК является NP-полной. Это означает, что если известная гипотеза о классах задач P  NP все-таки верна, то алгоритма полиномиальной сложности для ЗК не существует.

Задача коммиваяжера (оптимизационный вариант)

Пусть имеем полный n-вершинный взвешенный по ребрам граф K_n . Пусть (x) - взвешивающая целочисленная функция (функция стоимости), где xX , X - множество ребер графа. Рассматриваем т.н. закрытую ЗК: требуется найти простой цикл C, покрывающий все вершины графа и имеющий минимальную стоимость L_С:

, (1)

где S_C - пространство гамильтоновых циклов графа K_n .

Ограничимся случаем, когда функция (x) представлена симметричной матрицей весов ребер (ЗК с симметричной матрицей).

Ниже приводятся примеры построения двух двух приближенных алгоритмов решения задачи КО для матриц произвольного вида: пошагового алгоритма с регулируемой глубиной просмотра (РГ-алгоритм) и алгоритма с выделением оптимального реберного подмножества (ОР-алгоритм).

РГ-алгоритм

Алгоритм базируется на следующей идее. Пусть С представляет собой уже сформированную часть искомого гамильтонового цикла. На каждом шаге алгоритма просматриваются все маршруты (простые цепи), являющиеся возможным продолжением С и содержащие k вершин (k - задано), выбирается наилучший среди них и ближайшая вершина из найденного продолжения присоединяется к С. Ниже приводится детальное описание алгоритма.

Вход: полный граф K_n с множеством вершин V и множеством ребер X , n - число вершин, функция весов ребер (x) , xX , (x)Z⁺ , глубина просмотра k , kZ⁺.

Выход: гамильтонов цикл C и его стоимость L(C), удовлетворяющие условию (2).

Обозначения: m - число вершин, включенных в искомый маршрут С в данный момент.

1. Включить в искомый маршрут С вершину графа с номером 1. Величине m присвоить значение 1.

2. Если m+k = n , идти к п. 3, иначе - к п. 4.

3. Сформировать множество всех простых цепей, включающих k+1 вершин и при этом таких, у которых начальной вершиной является последняя вершина, включенная в маршрут С , а конечной - вершина с номером 1. Выбрать простую цепь минимальной длины и присоединить ее к имеющемуся маршруту С. Процесс завершен.

4. Сформировать множество всех простых цепей, включающих k вершин и с началом в вершине, которая была включена в маршрут С последней. Выбрать простую цепь минимальной длины. Вторую вершину найденной цепи включить в маршрут С. Увеличить m на единицу и перейти к п. 2.

Из описания приведенного выше алгоритма можно получить, что функция его временной сложности имеет следующий вид (попробуйте доказать самостоятельно):

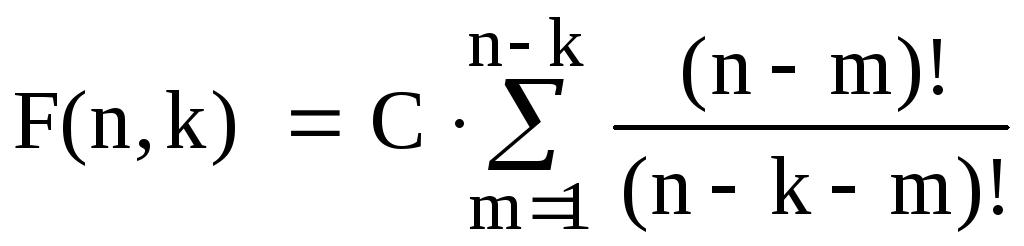. (3)

При минимальной глубине просмотра ( k = 1) описанный алгоритм соответствует методу решения задачи КО, хорошо известному как алгоритм "иди в ближайший". Для рассматриваемого алгоритма это самое грубое приближение. Действительно, для k = 1 имеем:

.

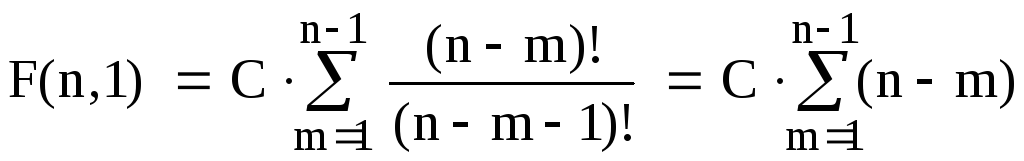Обозначим j = n - m , тогда

При максимальной глубине просмотра k = n-1 получаем точное решение и процедуру полного перебора гамильтоновых циклов. Алгоритм будет иметь факториальную сложность:

(5)

Таким образом, при увеличении глубины просмотра от 1 до n-1 сложность алгоритма постепенно изменяется от полиномиальной до факториальной, а получаемое решение приближается к точному.

ОР-алгоритм

Описание этого алгоритма выглядит следующим образом. Пусть Х - множество ребер, а V - множество вершин графа K_n , на котором решается задача КО. Пусть Y - рабочее подмножество, Y X .

1. Положить Y =  .

2. Найти ребро xX с наименьшим весом и включить его в текущее подмножество Y. Исключить x из множества X .

3. Проверить, является ли граф g = (V,Y) гамильтоновым. Если нет, идти к п. 2, в противном случае идти к п.4.

4. Найти решение задачи КО на графе g.

Отметим, что так как исходный граф является полным, алгоритм завершается после конечного числа шагов. Сокращение объема вычислений имеет место в результате того, что задача КО решается на графе, который не является полным и содержит ограниченное число гамильтоновых циклов. Алгоритм дает приближенное решение задачи.