• Робота сил поля тяжіння. Потенціал

Я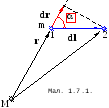кщо тіло переміщується під дією сили тяжіння, то при цьому виконується робота. Давайте знайдемо роботу сил тяжіння при русі матеріальної точки масою у полі тяжіння, створеного точковою масою . При елементарному переміщенні на величину (Мал. 1.7.1) робота складатиме:

==-

(1.7.15)

де =, знак „-” вказує на те, що напрям сили тяжіння протилежний напряму радіуса-вектора рухомої точки . Роботу сил тяжіння при переміщенні тіла з точки 1 в точку 2, радіуси яких і :

==-

(1.7.16)

Отже, з (1.7.16) видно, що робота сил тяжіння не залежить від форми шляху. Сили тяжіння – консервативні, або потенціальні. Якщо , то тіло віддаляється від тіла як джерела поля тяжіння і робота . Отже, робота виконується проти сил тяжіння. Якщо ж , то тіло наближається до джерела і , тобто сили поля тяжіння виконують додатну роботу.

Оскільки сили тяжіння консервативні, то виконана цими силами робота переміщення тіла в полі тяжіння дорівнює зміні потенціальної енергії тіла:

=-=-.

(1.7.17)

При переміщенні матеріальної точки з нескінченості на відстань від тіла масою , потенціальна енергія точки буде:

=-.

(1.7.18)

При такому вигляді формули (1.7.18) потенціальна енергія двох матеріальних точок, що взаємодіють, завжди від’ємна і зростає при збільшенні відстані між ними. Якщо ж ми поділимо ліву і праву частину (1.7.18) на масу тіла , то отримаємо величину:

=-=,

(1.7.19)

яка не залежить від маси , а залежить тільки від маси і відстані від цього тіла до точки поля – потенціал поля тяжіння – скалярна величина. Потенціал є енергетичною характеристикою поля тяжіння. Враховуючи поняття потенціалу:

=,

(1.7.20)

де і - потенціали точок 1 і 2. Потенціал точки поля тяжіння, створеного системою матеріальних точок, визначається алгебраїчним сумуванням.

Оскільки потенціал величина скалярна, завжди існують поверхні, точки яких мають однакові потенціали – це еквіпотенціальні поверхні.

У зв’язку з тим, що напруженість і потенціал являють собою характеристики одного і того самого поля, то між ними повинен існувати зв’язок. Продиференцюємо по :

=.

(1.7.21)

Вираз для напруженості гравітаційного поля з урахуванням (1.7.21) перепишемо так:

=-=-..

(1.7.22)

Величина = - це одиничний вектор, який незалежно від вибору нульового потенціалу завжди напрямлений у бік зростання потенціалу. У векторному аналізі величину називають градієнтом потенціалу:

=-.

(1.7.23)

– зв’язок напруженості і потенціалу гравітаційного поля.

Про рішення задачі двох тіл, на прикладі пружного та не пружного співударів ви дізнаєтеся самостійно з підручників [4,6,7-9], та під час виконання лабораторного практикуму з фізики.

Прикладом центрального поля тяжіння є поле, що створюється нерухомою матеріальною точкою.

Давайте розглянемо рух тіл у центральному поля тяжіння. До таких рухів належать рухи планет Сонячної системи. При цьому Сонце і планети вважають матеріальними точками. Спростимо ще задачу. Розглянемо рух тіл у центральному полі тяжіння, застосувавши закон збереження енергії. Якщо тіло масою рухається у центральному полі, створеному джерелом поля масою , то його повна енергія визначатиметься так:

=-=.

(1.7.24)

Момент імпульсу тіла масою буде:

==

(1.7.25)

З означення центрального поля випливає, що сила, яка діє на рухому в ньому матеріальну точку, завжди проходить через центр поля. при цьому плече сили відносно центра поля дорівнюватиме нулю. Отже, момент імпульсу тіла масою є величина стала:

=

(1.7.26)

д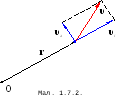 е = - кутова швидкість. Повну швидкість руху тіла можна розкласти на радіальну та азимутальну = складові (Мал.1.7.2). Тоді кінетичну енергію тіла перепишемо у наступному вигляді:

=+=+

(1.7.27)

Повна енергія:

-+==

(1.7.28)

Оскільки в цьому рівнянні тільки перший доданок залежить від швидкості, то роль потенціальної енергії відіграє функція:

=-+.

(1.7.29)

Давайте тепер знайдемо умови, при яких траєкторія руху тіла стане еліптичною, тобто коли рух тіла буде обмежений у деякій області простору. Такий рух ще називають фінітним. Для розв’язання цієї задачі застосуємо графічний метод. На малюнку 1.7.3 штрихованою лінією наведемо графіки функцій:

=-; = ()

(1.7.30)

Суцільною лінією наведемо графік функції , як результат додавання ординат функцій і . З Мал. 1.7.3 видно, що для функція додатна і при асимптотично наближається до . Для значень функція від’ємна і при вона асимптотично наближається до нуля.

Оскільки величина завжди додатна, то межі області, в якій може перебувати тіло, визначаються умовою . Проведемо на Мал. 1.73 прямі == для випадку, коли і .

У першому випадку ділянки кривої (), що знаходяться над прямою, не можуть бути досягнуті тілом з енергією . У другому випадку () пряма перетинає криву у двох точках А і В. Їм відповідають радіуси і . Вони і визначають межі області, в якій рухається тіло у центральному гравітаційному полі. Саме у цьому разі рух тіла буде обмеженим, тобто фінітним. Траєкторія руху при цьому буде еліптичною.

Якщо , то пряма перетинає криву тільки в одні точці, які відповідає радіус . Якщо ж тіло рухається справа наліво, то на відстані його напрям руху зміниться на протилежний.

Рух тіла буде необмеженим, тобто ін фінітним, а траєкторія - гіперболічною. Якщо =, то рух тіла також буде необмеженим, а траєкторія – параболічною.

Всі наведені висновки можна повністю поширити на рух штучних супутників Землі та космічних кораблів. Про це ви дізнаєтеся самостійно з будь-якого підручника в переліку літератури.