Фізика / Лекции / Механика / 1-2 К_нематика обертального руху

Херсонський національний технічний університет Кафедра загальної та прикладної фізики

КІНЕМАТИКА ОБЕРТАЛЬНОГО РУХУ Лекція 1.2.

	1.2. КІНЕМАТИКА ОБЕРТАЛЬНОГО РУХУ
	РУХ ПО КОЛУ*
	КІНЕМАТИКА ОБЕРТАЛЬНОГО РУХУ
СПІВВІДНОШЕННЯ МІЖ ЛІНІЙНИМИ ТА КУТОВИМИ ВЕЛИЧИНАМИ

• РУХ ПО КОЛУ

Розглянемо, як окремий випадок криволінійного руху 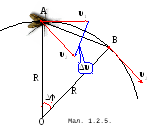рівномірний рух матеріальної точки по колу радіуса з центром (Мал.1.2.1). При цьому швидкість руху точки залишається сталою за величиною, а змінюється за напрямом. Нехай за малий проміжок часу матеріальна точка перемістилась з точки траєкторії в точку . Зміна швидкості за напрямом при цьому характеризуватиметься вектором , який визначаємо паралельним перенесенням і відкладенням з точки вектора (Мал.1.2.1). Трикутник і трикутник зі сторонами , , - подібні. З їхньої подібності маємо:

= або =

(1.2.1)

Поділивши обидві частини на і перейшовши до границі, маємо:

= або =

(1.2.2)

Звідси маємо:

=.

(1.2.3)

Оскільки при кут , то і вектор буде перпендикулярним до вектора швидкості в точці траєкторії (), тобто напрямленим по радіусу до центра. Таке прискорення називатимемо доцентровим. Отже, при рівномірному русі матеріальної точки по колу тангенціального прискорення немає, а повне прискорення дорівнює доцентровому.

• КІНЕМАТИКА ОБЕРТАЛЬНОГО РУХУ

При обертальному русі твердого тіла навколо нерухомої осі всі його точки описують кола, центри яких лежать на осі обертання (Мал.1.2.2). Проведемо через вісь обертання дві площини 1 і 2. Одну з них (2) жорстко зв’яжемо з тілом, а другу (1) вважатимемо нерухомою. Обертання тіла навколо осі можна задати за допомогою кута між цими площинами. Якщо за проміжки часу тіло здійснило обертання на кут , то границю, до якої прямує відношення при , називають миттєвою кутовою швидкістю, або просто кутовою швидкістю.

===.

(1.2.4)

Обертання тіла із сталою кутовою швидкістю називатимемо рівномірним. Нерівномірне обертання тіла характеризуватиме за допомогою кутового прискорення. Якщо за малий проміжок часу кутова швидкість змінилася на величину , то границя, до якої прямує відношення при , називатимемо миттєвим кутовим прискоренням, або просто прискоренням:

===

(1.2.5)

З урахуванням (1.2.4):

===

(1.2.6)

При обертальному русі всі точки твердого тіла мають однакові кутові швидкості і кутове прискорення. Кутову швидкість і кутове прискорення вимірюють:

=; =

(1.2.7)

• СПІВВІДНОШЕННЯ МІЖ ЛІНІЙНИМИ ТА КУТОВИМИ ВЕЛИЧИНАМИ

Встановимо співвідношення між лінійною і кутовою швидкостями та лінійним і кутовим прискоренням. Довжина дуги , яку описує точка, що знаходиться на відстані від осі при обертанні на кут :

=

(1.2.8)

Поділимо на . При матимемо:

= або =.

(1.2.9)

На основі формул (1.2.3) та (1.2.9) отримаємо, що нормальне прискорення:

==

(1.2.10)

Тангенціальне прискорення:

==()=

(1.2.11)

З рівнянь (1.2.10) та (1.2.11) видно, що як нормальне так і тангенціальне прискорення пропорційне відстані від осі обертання . Модуль повного прискорення точки тіла:

=

(1.2.11)

Отже, знаючи кутову швидкість і кутове прискорення тіла, що обертається, а також відстань від осі обертання, можна визначити величину і напрям прискорення будь-якої точки тіла. Оскільки відношення тангенціального прискорення до нормального:

=

(1.2.12)

є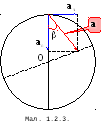 однаковим для всіх точок тіла, то вектор повного прискорення для всіх точок тіла утворює з радіусом, проведеним до цієї точки, один і той самий кут (мал.1.2.3).

При обертальному русі кутова швидкість і кутове прискорення визначаються однозначно тоді, коли відоме розташування в просторі осі обертанні і вказано напрям обертання навколо неї.

Оскільки лінійна швидкість і лінійне прискорення – векторні величини, а крім того між величинами , , , і існує взаємозв’язок у вигляді формул (1.2.9)-(1.2.12), то кутову швидкість і кутове прискорення доцільно визначати як вектори.

В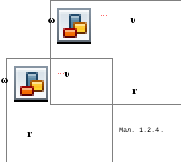ектор кутової швидкості зображують відрізком прямої, яка збігається з віссю обертання. Довжина цієї прямої в певному масштабі виражає величину кутової швидкості. Цей зв’язок умовились встановлювати за правилом правого гвинта: вектор кутової швидкості напрямлений вздовж осі обертання в бік поступального руху гвинта, коли його обертати за напрямом обертання (Мал.1.2.4). Такий вектор називають осьовим або аксіальним. Оскільки кутова швидкість – вектор, зміна кутової швидкості є також вектором. Отже, кутове прискорення – також вектор, який збігається за напрямом з вектором .

В разі, коли орієнтація осі обертання з часом не змінюється, вектор кутового прискорення при збільшення кутової швидкості збігається з вектором кутової швидкості. При зменшенні кутової швидкості напрями векторів кутового прискорення і кутової швидкості протилежні. Запишемо співвідношення (1.2.9)-(1.2.12) у векторній формі. Для цього розглянемо радіус обертання точки як вектор, напрямленій від осі обертання. На основі означення векторного добутку (лекція 0.1):

=[х]	(1.2.13)
=[х]	(1.2.14)
=-	(1.2.15)

На Мал.1.2.5 показано розташування векторів , , , , , . Знак мінус у формулі (1.2.15) вказує на те, що нормальне прискорення напрямлене по радіусу до центра. Введення векторів кутової швидкості і кутового прискорення є доцільним також тому, що у разі, коли тіло одночасно бере участь у двох обертаннях, його результуюче обертання характеризується саме цими векторами, які дістанемо завдяки додаванню за правилом паралелограма. Приклад розглянутий у [5] на стор. 16.

Обертання характеризується також періодом обертання і частотою обертання . Період обертання – час, протягом якого тіло робіть повний оберт навколо осі обертання, а частота (лінійна частота) – кількість обертів, які здійснює тіло за одиницю часу. Між періодом і частотою обертання існує простий зв’язок:

=

(1.2.16)

Оскільки за період тіло здійснює повний поворот на кут =:

==

(1.2.17)

• ЛІТЕРАТУРА

1. Кудрявцев П.С. Курс истории физики. – М.: Просвещение, 1982.–448 С.

2. Храмов Ю.А. Физики: биографический справочник.–К.: Наукова думка, 1977.–511с.

3. Савельев И.В. Курс общей физики. Т.1. Механика. Молекулярная физика. – М.: Наука, 1987. – 432 с.

4. Бушок Г.Ф., Левандовський В.В., Півень Г.Ф. Курс фізики. 1 кн. Фізичні основи механіки. Електрика і магнетизм. – К.: Либідь, 2001. – 448 с.

5. Кучерук І.М., Горбачук І.Т. Загальна фізика. 1 кн. Фізичні основи механіки. Молекулярна фізика і термодинаміка. – К.: Вища шк., 1995. – 431 с.

6. Зисман Г.А., Тодес О.М. Курс общей физики. Т.1. Механика. Молекулярная физика. – М.: Наука, 1974.

7. Гершензон Е.М., Малов Н.Н. Курс общей физики. Механика. - М.: Просвещение, 1987. – 307 С.

8. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Т.1.– М.: Мир.

9. Киттель Ч., Найт У., Рудерман М. БКФ. Механика. - М.: Наука, 1975. – 480 С.

10. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высш. шк.., 1989. – 608 с.

11. Кузьмичев В.Е. Законы и формулы физики. Справочник. – Киев: Наук. думка, 1989. – 864 с.

12. Иродов И.Е. Основы классической механики. – М.: Высш. шк.

13. Голдстейн Г. Классическая механика.

14. Савельев И.В. Курс физики. В 3-х томах. Т.1. Механика. Молекулярная физика.– М.: Наука, 1989. – 352 с.

Факультет машинобудування
Лектор Дон Н.Л.		стор. 5 з 5