II. Статистичний аналіз генеральної сукупності

Завдання 1. Розраховані в табл. 1.3 генеральні показники представлені в табл. 1.10.

Таблиця 1.10

Описові статистики генеральної сукупності

Узагальнюючі статистичні показники сукупності за ознаками, що вивчаються	Ознаки
	вартість активів	фінансовий результат
Стандартне відхилення ,млн. грн.
Дисперсія
Асиметричність As
Ексцес Ek

Для нормального розподілу справедлива рівність

R_N=6N.

В умовах близькості розподілу одиниць генеральної сукупності до нормального це співвідношення використовується для прогнозної оцінки розмаху варіації ознаки в генеральній сукупності.

Очікуваний розмах варіації ознак R_N:

- для першої ознаки R_N =..................,

- для другої ознаки R_N =..................

Співвідношення між генеральною і вибірковою дисперсіями:

- для першої ознаки 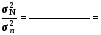.., тобто розбіжність між дисперсіями незначна (значна);

- для другої ознаки 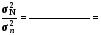.., тобто розбіжність між дисперсіями незначна (значна).

Завдання 2. Застосування вибіркового методу спостереження пов'язане з вимірюванням міри достовірності статистичних характеристик генеральної сукупності, отриманих за наслідками вибіркового спостереження. Достовірність генеральних параметрів залежить від репрезентативності вибірки, тобто від того, наскільки повно і адекватно представлені у вибірці статистичні властивості генеральної сукупності.

Як правило, статистичні характеристики вибіркової і генеральної сукупностей не збігаються, а відхиляються на деяку величину е, яку називають похибкою вибірки (похибкою репрезентативності). Похибка вибірки – це різниця між значенням показника, який був отриманий за вибіркою, і генеральним значенням цього показника. Наприклад, різниця

= |-|

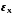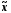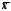визначає похибку репрезентативності для середньої величини ознаки.

Оскільки похибки вибірки завжди випадкові, обчислюють середню і граничну похибки вибірки.

1. Для середнього значення ознаки середня похибка вибірки 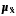(її називають також стандартною помилкою) виражає середнє квадратичне відхилення вибіркової середньої 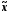від математичного очікуванняM[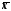] генеральної середньої .

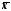Для ознак, що вивчаються, середні похибки вибірки 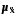наведені в таблиці 3:

- для ознаки вартість активів

=.......,

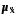- для ознаки фінансовий результат

=........

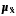2. Гранична похибка вибірки 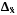визначає межі, в межах яких лежить генеральна середня 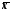. Ці межі задають так званийдовірчий інтервал генеральної середньої 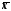– випадкову область значень, яка з ймовірністю P, близькою до 1, гарантовано містить значення генеральної середньої. Цю ймовірність називають довірчою ймовірністю або рівнем надійності.

Для рівнів надійності P=0,954; P=0,683 оцінки граничних похибок вибірки 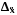подано в таблицях 1.3 і 1.4.

Для генеральної середньої граничні значення і довірчі інтервали визначаються виразами:

,

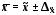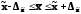
Граничні похибки вибірки і очікувані межі для генеральних середніх подані в таблиці 11.

Таблиця 1. 11

Граничні похибки вибірки і очікувані межі для генеральних середніх

Ймовірність Р	Коефі-цієнт довіри t	Граничні похибки вибірки, млн. грн.		Очікувані межі для середніх, млн. грн.
		для першої ознаки	для другої ознаки	для першої ознаки	для другої ознаки
0,683	1
0,954	2

Висновок:

Збільшення рівня надійності веде до розширення (звуження) очікуваних меж для генеральних середніх.

Завдання 3. Розраховані в табл. 1.3 значення коефіцієнтів асиметрії As і ексцесу Ek дані в табл. 1.10.

1.Показник асиметрії As оцінює зміщення ряду розподілу вліво або вправо по відношенню до осі симетрії нормального розподілу.

Якщо асиметрія правостороння (As>0) те права частина емпіричної кривої виявляється довше лівої, тобто має місце нерівність 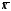>Me>Mo, що означає переважну появу в розподілі вищих значень ознаки (середнє значення 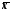більше серединногоMe і модального Мо).

Якщо асиметрія лівостороння (As<0), то ліва частина емпіричної кривої виявляється довше правої і виконується нерівність 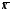<Me<Mo, що означає, що в розподілі частіше зустрічаються нижчі значення ознаки (середнє значення 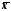менше серединного Me і модального Мо).

Чим більше величина |As|, тим більше асиметричний розподіл. Оцінна шкала асиметрії:

|As| 0,25 - асиметрія незначна;

0,25<|As|0,5 - асиметрія помітна (помірна);

|As|>0,5 - асиметрія істотна.

Висновок:

Для ознаки вартість активів спостерігається незначна (помітна, істотна) лівостороння (правостороння) асиметрія. Отже, в розподілі переважають ..................................

Для ознаки фінансовий результат спостерігається незначна (помітна, істотна) лівостороння (правостороння) асиметрія. Отже, в розподілі переважають ........................................................

2.Показник ексцесу Ek характеризує крутизну кривої розподілу - її загостреність або пологість у порівнянні з нормальною кривою.

Як правило, коефіцієнт ексцесу обчислюється тільки для симетричних або близьких до них розподілів.

Якщо Ek>0, то вершина кривої розподілу розташовується вище за вершину нормальної кривої, а форма кривої є більш гостровершинною, ніж нормальна. Це говорить про скупчення значень ознаки в центральній зоні ряду розподілу, тобто про переважну появу серед даних значень, близьких до середньої величини.

Якщо Ek<0, то вершина кривої розподілу лежить нижче за вершину нормальної кривої, а форма кривої пологіша в порівнянні з нормальною. Це означає, що значення ознаки не концентруються в центральній частині ряду, а розсіяні по всьому діапазону від x_max до x_min.

Для нормального розподілу Ek=0. Чим більше абсолютна величина |Ek|, тим істотніше розподіл відрізняється від нормального.

При незначному відхиленні Ek від нуля форма кривої емпіричного розподілу трохи відрізняється від форми нормального розподілу.

Висновок:

1. Оскільки для ознаки Вартість активів Ek>0 (Ek<0), то крива розподілу є більш гостровершинною (пологовершинною) в порівнянні з нормальною кривою. При цьому Ek трохи (значно) відрізняється від нуля (Ek=|.........|) Отже, за даною ознакою форма кривої емпіричного розподілу значно (трохи) відрізняється від форми нормального розподілу.

2.Оскільки для ознаки Фінансовий результат Ek>0 (Ek<0), то крива розподілу є більш гостровершинною (пологовершинною) в порівнянні з нормальною кривою. При цьому Ek трохи (значно) відрізняється від нуля (Ek=|..........|). Отже, за даною ознакою форма кривої емпіричного розподілу значно (трохи) відрізняється від форми нормального розподілу.