2. Висновки за наслідками виконання лабораторної роботи1

I. Статистичний аналіз вибіркової сукупності

Завдання 1.

Висновок:

Кількість аномальних одиниць спостереження (табл.1.2) рівна .............,

Це - номери та назви банків..................................................................................

Завдання 2. Розраховані вибіркові показники представлені в двох таблицях — табл. 1.3 і табл. 1.5. На основі цих таблиць формується єдина таблиця (табл. 1.8) значень вибіркових показників, які перераховані в умові Завдання 2.

Таблиця 1.8

Описові статистики вибіркової сукупності комерційних банків України

Узагальнюючі статистичні показники сукупності за ознаками, що вивчаються	Ознаки
	Вартість активів	Фінансовий результат
Середня арифметична (),млн. грн.
Мода (Мо), млн. грн.
Медіана (Ме), млн. грн.
Розмах варіації (R), млн. грн.
Дисперсія ()
Середнє квадратичне відхилення (), млн. грн.
Коефіцієнт варіації (Vу) %

Завдання 3.

3а). Ступінь варіації ознаки визначається за значенням коефіцієнта варіації V відповідно до оцінної шкали варіації ознаки:

0%<V40% - варіація незначна;

40%< V60% - варіація середня (помірна);

V>60% - варіація значна.

Висновок:

Для ознаки вартість активів показник V =..... . Оскільки значення показника лежить у діапазоні ........... оцінної шкали, то, варіація............. .

Для ознаки фінансовий результат показник V =.... . Оскільки значення показника лежить у діапазоні ........... оцінної шкали, то, варіація............. .

3б). Ступінь однорідності сукупності за ознакою, що вивчається, для нормального і близьких до нормального розподілів встановлюється за значенням коефіцієнта варіації V. Якщо V33%, то за даною ознакою розбіжності між значеннями ознаки невеликі. Якщо при цьому одиниці спостереження відносяться до одного певного типу, то сукупність, що вивчається, однорідна.

Висновок:

Для ознаки вартість активів показник 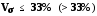отже, за даною ознакою вибіркова сукупність ........... .

Для ознаки фінансовий результат показник отже, за даною ознакою вибіркова сукупність ........... .

3в). Для оцінки кількості попадань індивідуальних значень ознаки x_i у той або інший діапазон відхилення від середньої , а також для виявлення структури розсіювання значеньx_i після 3-го діапазону формується табл. 1.9 (з конкретними числовими значеннями меж діапазонів).

Таблиця 1.9

Розподіл значень ознаки по діапазонах розсіяння ознаки відносно

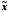
		Межі діапазонів, млн. грн.			Кількість значень xi, що знаходяться в діапазоні			Процентне співвідношення розсіювання значень xi за діапазонами, %
		Перша ознака		Друга ознака	Перша ознака		Друга ознака	Перша ознака		Друга ознака
А	1		2	3		4	5		6
	[.....;.....]		[.....;....]
	[.....;.....]		[.....;....]
	[.....;.....]		[.....;....]

На основі даних табл. 1.9 структура розсіювання значень ознаки за трьома діапазонами (колонки 5 і 6) зіставляється із структурою розсіювання за правилом «трьох сигм», справедливим для нормальних і близьких до нього розподілів:

68,3% значень розташовуються в діапазоні (),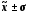

95,4% значень розташовуються в діапазоні (),

99,7% значень розташовуються в діапазоні ().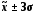

Якщо отримана в таблиці 1.9 структура розсіювання х_i після 3-го діапазону трохи розходиться з правилом «трьох сигм», можна припустити, що розподіл одиниць сукупності за даною ознакою близький до нормального.

Розбіжність з правилом «трьох сигм» може бути істотною. Наприклад, менше 60% значень х_i потрапляють у центральний діапа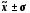зон () або більше 5% значеньх_i виходить за діапазон (). У цих випадках розподіл не можна вважати за близький до нормального.

Висновок:

Порівняння даних колонки 5 табл. 1.9 за правилом «трьох сигм» показує на їх незначну (істотну) розбіжність, отже, розподіл одиниць сукупності за ознакою вартість активів можна (не можна) вважати близьким до нормального.

Порівняння даних колонки 6 табл. 1.9 за правилом «трьох сигм» показує на незначну (істотну) розбіжність, отже, розподіл одиниць сукупності за ознакою фінансовий результат можна (не можна) вважати близьким до нормального.

Завдання 4. Для відповіді на питання 4а) – 4в) необхідно скористатися табл.1.8 і порівняти величини показників для двох ознак.

Для порівняння ступеня варіації значень ознак, що вивчаються, ступеня однорідності сукупності за цими ознаками, надійності їх середніх значень використовуються коефіцієнти варіації V ознак.

Висновок:

Оскільки V для першої ознаки більше (менше), ніж V для другої ознаки, то варіація значень першої ознаки більше (менше) варіації значень другої ознаки, сукупність більш однорідна за першою (другою) ознакою, середнє значення першої ознаки є (менш) надійнішим, ніж у другої ознаки.

Завдання 5. Інтервальний варіаційний ряд розподілу одиниць сукупності за ознакою вартість активів представлений у табл. 1.7, а його гістограма і кумулята – на рис. 1.2.

Можливість віднесення розподілу ознаки «вартість активів» до нормального розподілу встановлюється шляхом аналізу форми гістограми розподілу. Аналізується кількість вершин в гістограмі, її асиметричність і вираженість «хвостів», тобто частоти появи в розподілі значень, що виходять за діапазон ().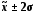

1. При аналізі форми гістограми, перш за все, слід оцінити розподіл варіантів ознаки за інтервалами (групами). Якщо на гістограмі чітко простежуються два-три «горби» частот варіантів, це говорить про те, що значення ознаки концентруються відразу в декількох інтервалах, що не відповідає нормальному закону розподілу.

Якщо гістограма має одновершинну форму, є підстави припускати, що вибіркова сукупність може мати характер розподілу, близький до нормального.

2. Для подальшого аналізу форми розподілу використовуються описові параметри вибірки – показники центру розподілу (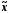,Мо, Me) і варіації (). Сукупність цих показників дозволяє дати якісну оцінку близькості емпіричних даних до нормальної форми розподілу.

Нормальний розподіл є симетричним, і для нього виконуються співвідношення:

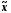=Mo=Me

Порушення цих співвідношень свідчить про наявність асиметрії розподілу. Розподіли з невеликою або помірною асиметрією в більшості випадків відносяться до нормального типу.

3. Для аналізу довжини «хвостів» розподілу використовується правило «трьох сигм». Згідно цього правила в нормальному і близьким до нього розподілах крайні значення ознаки (близькі до х_min і х_max) зустрічаються багато рідше (5-7 % всіх випадків), ніж, ті, що знаходяться в діапазоні ().Отже, за відсотком виходу значень ознаки за межі діапазону (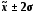) можна судити про відповідність довжини «хвостів» розподілу нормальному закону.

Висновок:

1. Гістограма є одновершинною (багатовершинною).

2. Розподіл приблизно симетричний (істотно асиметричний), оскільки параметри 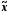, Мо, Me відрізняютьсятрохи (значно):

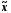= .............., Mo=.............., Me=..............

3. “Хвости” розподілу не дуже довгі (є довгими), оскільки згідно колонки 5 табл. 1.9.....% варіантів лежать за межами інтервалу (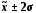)=(......;......) млн. грн.

Отже, на підставі п.п. 1,2,3, можна (не можна) зробити висновок про близькість розподілу, що вивчається, до нормального.