4.12. Параметрический анализ

Для практического внедрения результатов оптимизации полученное решение должно быть дополнено всесторонним анализом, который позволяет предсказать поведение оптимального решения при тех или иных возможных изменениях в модели.

Анализ чувствительности по переменным проводится по относительным оценкам. Оценка показывает скорость ухудшения значения критерия при отклонении значения переменной от оптимального. Очевидно, что точность реализации оптимальных значений должна быть тем выше, чем больше по абсолютной величине относительная оценка.

Влияние изменения отдельного ресурса в окрестности исходного значения устанавливается по двойственным переменным в оптимальном решении.

Вариантный анализ заключается в исследовании поведения оптимального решения при измнении состава модели (смена критерия, снятие или добаление одного ограничения и т.п.).

Параметрический анализ (параметрическое программирование) применяется для определения изменения оптимального решения в общем случае при одновременном и непрерывном изменении нескольких коэффициентов модели (в частном случае может изменяться только один). При этом характер изменения коэффициентов задается параметрически как функция одного параметра, а интересуемый диапазон изменения значительно шире окрестности исходных значений. В параметрическом программировании рассматривается параметрирование правой части, коэффициентов линейной формы, совместно коэффициентов критерия и правых частей, параметрирование отдельных столбцов или строк матрицы условий и другие более общие случаи совместного изменения коэффициентов.

Наибольший интерес представляют первые две задачи параметрирования, так как на практике нередки ситуации с изменением ресурсов (правых частей), цен или удельных затрат (кэффициентов критерия). Для них параметрическое решение можно найти в общем виде при линейной зависимости именений от параметра, а в отдельных случаях – и при нелинейной.

4.12.1. Параметрирование вектора ограничениий

Пусть оптимальное решениеX^* получено для вектора . Поставим вопрос: как будет изменяться оптимальное решение при изменении правой части, заданном параметрическиB()?

Рассмотрим только случай линейной зависимости

B()=B+V, (4.41)

где 0 – параметр, определяющий величину изменения вектора ограничений;

V– вектор размерностиm, определяющий направление и относительную скорость изменения компонентов вектора ограничений. Этот вектор задается ЛПР исходя из прогноза возможных изменений ресурсов.

Например, для трехмерного вектора B изменения могут быть заданы в виде

,

то есть ожидается одновременное уменьшение первого и третьего ресурсов и увеличение второго ресурса. При этом абсолютная величина изменения первого ресурса в три раза, авторого в полтора раза больше, чем третьего.

Для любогобазисного решения условия задачи

AX=B

можно записать в виде

A_BX_B+A_HX_H=B,

где индексы “B” и “H” обозначают базисные и небазисные векторы (матрицы). Так как небазисные переменные равны нулю, то отсюда следует

A_BX_B=В

и, в частности, для оптимального решения

A^*_BX^*_B=В. (4.42)

Так как мы исходим из наличия решения X^*, то базисная матрица - неособенная и существует обратная к ней матрица , умножая на которую слева равенство (4.42), получаем.

. (4.43)

Очевидно, что если заменить в (4.42) B наB() при =0, то ничего не изменится. При невырожденном оптимальном решении малое изменение B (>0 мало) не изменяет базис: оптимальная вершина хотя и смещается, но образуется теми же ограничениями. Поэтому в данном случае изменяется только оптимальное решение. Оптимальное решение при >0 обозначим X^**. Тогда для малых равенство (4.42) запишется в виде

,

откуда находим изменяемое оптимальное решение

С учетом (4.43) окончательно имеем

(4.44)

где

(4.45)

Таким образом, при линейном характере изменений ресурсов оптимальные значения переменных также меняются линейно. Однако это справедливо до тех пор, пока не происходит смена базиса. В невырожденном решении всегда найдется >0, при котором базис не меняется.Из выражения (4.44) следует, что при неотрицательном векторе P возрастание не может привести к уменьшению какой-либо базисной переменной и, значит, к смене базиса. В этом случае формула (4.44) справедлива для любых>0. Такая ситуация показана на рис. 4.12, где изменениеb₁ и b₂ в направлении стрелок не приводит к смене базиса (вершины, в которой достигается оптимальное решение).

Если же среди компонент вектора Р есть отрицательные, то соответствующие базисные переменные с увеличением будут уменьшаться. Если хотя бы одна из переменных обратится в нуль, то произойдет смена базиса и, следовательно, изменится обратная матрица. Формула (4.44) с исходными базисным решением и вектором Pстановится несправедливой. Этот случай иллюстрируется рис. 4.13., где оптимальная вершина сначала образована ограничениями по b₁ и b₂, а затем – ограничениями по b₁ и b₃.

Значение , при котором происходит смена базиса (базисного решения), называется критическим. Оно определяется по очевидной формуле

(4.46)

где p_i – компоненты вектораР.

Таким образом, исходное решение можно использовать для определения изменяемых решений по формуле (4.44) только в диапазоне

.

Отсюда получаем максимальное изменение правой части

Если диапазон изменения правой части недостаточен, то для его расширения необходимо заново решить задачу с векторомB₁=B+ΔB_max. Тогда получим новое оптимальное решение, новую обратную матрицу и на их основе снова проводится параметрирование дляB()=B₁+₁V. Повторяя эти действия, можно охватить весь желаемый диапазон изменения ресурсов. При этом соотношение компонент (но не знаков!) в вектореV может остаться исходным или измениться. В последнем случае зависимость от параметра на всем исследованном диапазоне будет кусочно-линейной.

Пример 4.7. Параметрируем задачу, решенную симплекс-методом в разд. 4.9.7 (пример 4.2) в предположении изменения 1-го и 4-го ресурсов.

Анализ поступления этих ресурсов показал, что первый может возрастать, а четвертый – уменьшаться, причем изменение четвертого может быть по абсолютной величине в два раза больше, чем первого. На этом основании записываем вектор изменений V=(1,0,0,-2).

Взяв обратную матрицу из оптимальной симплекс-таблицы (в столбцах начального базиса), по формуле (4.45) вычисляем вектор P:

Выписываем исходное оптимальное решение, соблюдая порядок базисных переменных в последней таблице:

Из данного порядка следует, что первый компонент вектора Pсоответствует 6-й переменной, а последний – первой. Таким образом, параметрическое решение запишется в виде

Так как вектор Pимеет отрицательные компоненты, вычисляем критическое значение

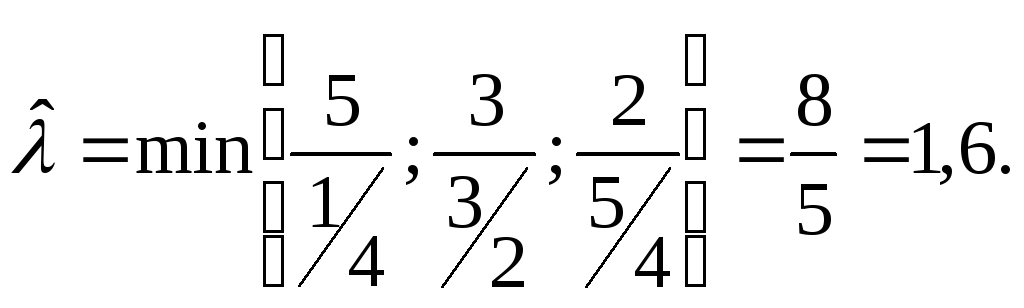
Оно позволяет определить критические отклонения ресурсов от исходных значений:

Следовательно, полученное параметрическое решение будет спаведливо при одновременном изменении ресурсов в диапазонах

19  b₁ < 20,6;

13,8 < b₄  17.

Чтобы расширить эти диапазоны, в задаче нужно заменить вектор B=(19; 13; 12;17) векторомB₁=(20,6;13;12;13,8) и снова решить ее. Новое решение параметрируется аналогичным образом.

Замечания. 1) Вместо принятого в примере вектора Vможно братьkV, где k – любое положительное число. При этом будет изменяться в k раз только а диапазоны измененияb_iостанутся прежними. 2) Очевидно, что если изменяется правая часть только в одном условии и в вектореV соответствующий компонент взят равным единице, то коэффициент при в параметрической записиL^** должен равняться двойственной переменной. При этом параметрический анализ позволяет определить диапазон изменения ресурса, в котором это значение двойственной переменной не меняется.