8.5. Задачи дробно-линейного программирования

Если целевая функция представляет собой отношение линейных функций, а все условия линейные, то задача относится к классу задач дробно-линейного программирования.

В общем случае целевая функция имеет вид

(8.28)

Такая функция легко преобразуется в линейную, если ее знаменатель при всех допустимых значениях переменных строго положителен. Для этого введем новую переменную r следующим образом

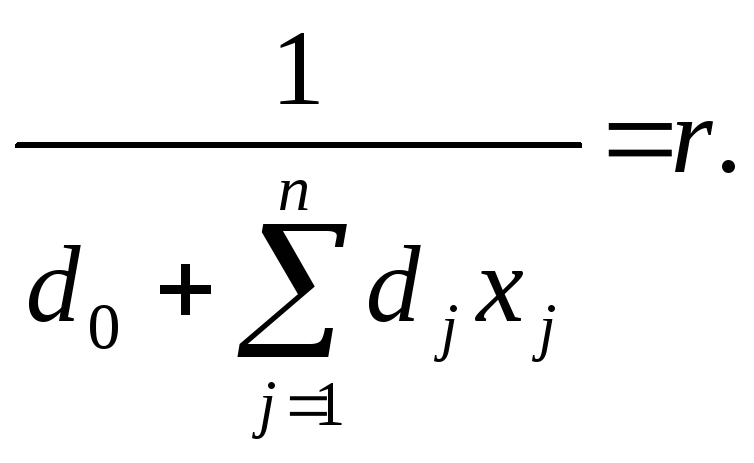(8.29)

Очевидно, что при оговоренном условии она может быть только больше нуля. Тогда функция (8.28) принимает вид

Произведя замену произведения переменных

(8.30)

окончательно имеем

(8.31)

Получили линейную функцию от n неотрицательных переменных y_j и одной положительной переменной r. Эта функция должна рассматриваться вместе с условием, следующим из (8.29):

или после замены (8.30)

(8.32)

Чтобы завершить построение эквивалентной линейной модели, следует ограничения задачи записать в новых переменных. Для этого умножим обе части каждого ограничения

на r:

и, произведя замену, получаем

(8.33)

В результате преобразований имеем задачу линейного программирования с критерием (8.31), ограничениями (8.32), (8.33) и переменными r>0, y_j 0, j. Получив ее решение одним из методов ЛП, вычисляем исходные переменные по очевидной формуле

Чтобы гарантировать выполнение условия положительности знаменателя, целесообразно вводить его явно в модель, то есть добавлять неравенство

где – очень малая положительная константа.

Возможность перехода к линейной задаче геометрически обусловлена тем, что линии уровня дробно-линейной функции описываются линейным уравнением. Действительно, пусть . Тогда из (8.28) следует

или

. (8.34)

Это обычное линейное уравнение относительно x_j. Поэтому линии уровня функции (8.28) в многомерном пространстве – гиперплоскости, а в двухмерном – прямые. Однако с изменением они не перемещаются параллельно, а поворачиваются вокруг множества вращения.

Множество вращения – это множество точек размерности n-2, образованное пересечением нулевых линий уровня числителя и знаменателя:

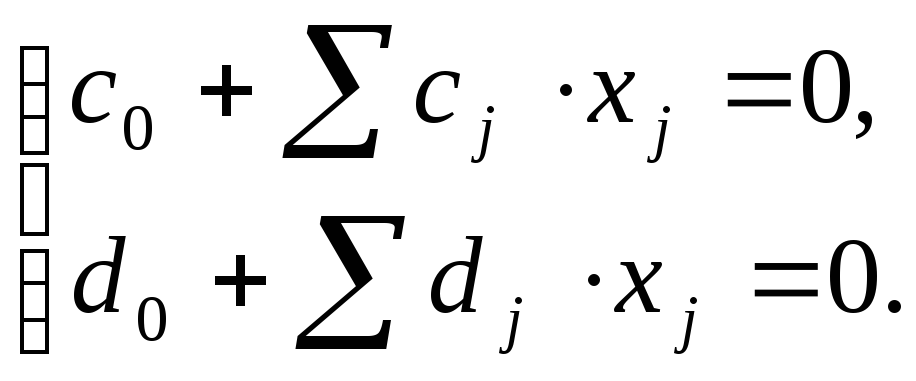
При n=2 оно состоит из одной точки, а при n=3 представляет собой прямую (ось вращения), образованную пересечением двух плоскостей.

Пример 8.5. Представим графически следующую задачу

;

3x₁ + 2x₂  6,

0 x₁  3,

0 x₂  3.

Уравнения нулевых линий уровня числителя и знаменателя образуют систему

из которой находим точку вращения: x₁=x₂=1/3. На рис. 8.6 это точка А. Нулевые линии показаны пунктиром, а направление поворота, в котором целевая функция возрастает, – стрелками. Отсюда ясно, что оптимальное решение достигается в вершине B:

8.6. Методы "спуска"

Так называются численные итерационные методы оптимизации, ориентированные на поиск минимума.

Общая схема решения заключается в генерации последовательности прибли­жений, асимптотически сходящейся к минимуму. Как правило, это локальный минимум, но в случае задач выпуклого программирования он является и глобальным. За конечное число итераций методы позволяют получить приближенное решение с заданной наперед точностью. Сходимость метода, как и скорость сходимости, зависят от свойств задачи и начального приближения. Скорость сходимости во многом определяет эффективность метода. Основными показателями эффективности (скорости сходимости) являются число итераций и число вычислений функции при прочих равных условиях. Количество итераций для одной и той же задачи сильно зависит о начального приближения (начальной точки) и требуемой точности. При этом количество необходимых итераций растет гораздо быстрее, чем точность.

При выборе метода следует учитывать свойства целевой функции: унимодальность или многоэкстремальнсть, дифференцируемость, выпуклость-вогнутость или их отсутствие и т. д. Кроме того, функции могут обладать “неприятными” для метода особенностями, такими как седловые точки и овражность. “Овраг” (при максимизации “гребень”) проявляются в том, что вдоль него функция изменяется намного слабее, чем в поперечном направлении. На карте линий уровня он виден по сильной вытянутости линий вдоль “дна” оврага с одновременной “сплющенностью” в поперечнике. Самым простым примером такой функции является эллипсоид

.

Приa>>b функция имеет овраг вдоль оси x₁, которая является его “дном” (рис.8.7).

Чем сильнее овражность и нелинейность “дна”, тем в большей степени замедляется скорость сходимости метода или возможен останов при недостижении окрестности минимума. Поэтому учет таких свойств особенно важен при выборе метода оптимизации.

Различают методы безусловной оптимизации, применяемые для нахождения минимума без ограничений на переменные, и условной оптимизации, когда поиск производится при наличии ограничений.

По информации, используемой для определения направления поиска, выделяют методы

•  нулевого порядка или прямые, если вычисляется только значение целевой функции;

•  первого порядка или градиентные, использующие первые производные (градиент);

•  второго порядка, требующие вычисления также вторых производных;

•  случайного поиска, применяющие механизм случайного выбора направления;

• генетические, сочетающие элементы детерминизма и случайности выбора;

•  комбинированные.

При оптимизации n-мерных функций часто используются методы одномерной минимизации. Поэтому сначала рассмотрим эти методы, затем многомерные методы безусловной оптимизации и, наконец, методы поиска условного минимума. Все приводимые ниже методы предназначены для минимизации унимодальных функций.