8.4. Сепарабельное программирование (сп)

В сепарабельном программировании рассматриваются задачи, в которых целевая функция и все функции ограничений сепарабельны.

Напомним, что функция многих переменных сепарабельна, если она имеет вид суммы функций отдельных переменных:

f(x₁, x₂, ..., x_n) = (8.18)

Линейные функции всегда сепарабельны и поэтому линейное программирование можно рассматривать как частный случай сепарабельного.

Решение задач СП основано на преобразовании в задачи линейного программирования путем аппроксимации нелинейных функций кусочно-линейными. Таким образом, исходная нелинейная задача заменяется аппроксимирующей линейной. Поэтому рассматриваемый метод является приближенным, а точность решения напрямую зависит от точности аппроксимации и теоретически может быть сколь угодно высокой.

Существует два основных способа записи аппроксимирующей задачи, отличающихся формой представления исходных переменных: в - или в -постановке.

 - постановка

Предполагается, что переменные, которые входят в модель нелинейно, ограничены снизу и сверху:

d_j  x_j  D_j. (8.19)

Для кусочно-линейной аппроксимации в этом диапазоне выбираются узловые точки, чаще в той части, где сильнее нелинейность функции. При этом первый узел совпадает с нижней границей, а последний – с верхней:

X_j1= d_j, = D_j,

где r_j – число интервалов по переменной x_j (r_j+1 – число узлов). Тогда рассматриваемая переменная x_j может быть выражена через новые переменные _jk в виде

, (8.20)

, (8.21)

. (8.22)

Выражение (8.20) называют уравнением сетки. С учетом (8.21) и (8.22) оно представляет переменную x_j в диапазоне (8.19) без потери точности. С использованием узловых точек и новых переменных кусочно-линейная функция, аппроксимирующая f_j(x_j), записывается в виде

(8.23)

где f_j(X_jk) – значение функции в узловых точках (рис. 8.5). Очевидно, что – функция, линей­ная относительно _jk. Пусть N – множество индексов нелинейных f_j(x_j). Тогда функция, аппрокси­мирующая f(X), имеет вид

(8.24)

Итак, чтобы построить линейную аппроксимирующую модель, необходимо:

1. для каждой переменной, входящей нелинейно, записать уравнение сетки;

2. во всей модели заменить переменные из п.1, входящие в линейные f_j , соответствующими уравнениями сетки;

3. все функции, содержащие нелинейности, представить в виде (8.24);

4. добавить ограничения (8.21), (8.22) для всех новых переменных.

Если переменная x_j входит нелинейно в несколько функций, узлы сетки выбираются с учетом нелинейности всех таких функций, так как для одной переменной может быть только одно уравнение сетки.

Поясним запись ограничений. Пусть имеется исходное ограничение

_ij (x_j)  b_i

со всеми нелинейными _ij. Тогда после аппроксимации оно принимает вид

В общем случае левая часть ограничения записывается аналогично (8.24).

Хотя аппроксимирующая задача линейная, получаемое на ней решение не всегда является приближением к решению исходной задачи. Дело в том, что одно и то же значение x_j можно получить по уравнению сетки при разных _jk, то есть представить через разные пары узлов. Например, некоторое значение x_j можно выразить через смежные узлы, в интервале которых находится значение, а можно через любую другую пару узлов, лежащих слева и справа, в том числе через первый и последний узел. Во всех случаях,кроме первого аппроксимация функции будет грубой и тем грубее, чем дальше отстоят узлы от данного значения x_j.

Отсюда следует правило смежных весов: из одного уравнения сетки отличными от нуля могут быть не более 2-х переменных_jk со смежными значениями k.

Если аппроксимирующая задача является задачей выпуклого программирования, то это правило выполняется автоматически и решение находится методом ЛП без каких-либо дополнений. Оптимальное решение аппроксимирующей задачи будет приближением глобального решения исходной задачи.

В противном случае алгоритм ЛП должен включать правило ограниченного ввода:

если в базисном решении находится _jk, то допустимыми для ввода могут быть только _jk+1 или _jk-1.

При этом нельзя утверждать, что получаемое решение является приближением к глобальному оптимуму исходной задачи. Скорее оно будет приближением локального оптимума.

Свойства задачи зависят от всех функций модели:

1. Если все ограничения линейные, то для выпуклости задачи достаточно, чтобы были вогнутыми все f_j критерия (выпуклы при минимизации

2. При нелинейности критерия и ограничений для выпуклости задачи должны быть вогнуты все f_j и выпуклы все _ij.

3. Если хотя бы одна f_j не вогнута при максимизации и/или одна _ij не выпукла, задача не является выпуклой.

Заметим, что, если все функции кусочно-линейные, переход к новым переменным не связан с потерей точности и при выполнении условий задач выпуклого программирования получаемое решение является точным и глобальным.

Пример 8.3. Задача

f = 6x₁ – x₁² + 7x₂  max,

2x₁² – 5x₁ + 3x₂²  8,

1  x₁ < 4, x₂  0

является задачей сепарабельного программирования. Здесь

f₁(x₁) = 6x₁ – x₁²; f₂(x₂) = 7x₂;

₁₁(x₁) = 2x₁² – 5x₁; ₁₂(x₂)=3x₂².

Так как f₁(x₁) и f₂(x₂) – вогнутые, а ₁₁(x₁) и ₁₂(x₂) – выпуклые, имеем задачу выпуклого программирования. Обе переменные входят нелинейно, поэтому нужно строить две сетки. Оценим верхний пределx₂:находимmin₁₁=-3.125, затем из ограничения получаем максимально возможное значениеx₂=1.93. Берем D₂=2. Пусть узловыми будут значения поx₁: 1, 2, 3, 4; по x₂: 0, 1, 2. Записываем уравнения сеток: x₁= ₁₁ +2₁₂+3₁₃+4₁₄, x₂=₂₂+2₂₃. В итоге получаем модель аппроксимирующей задачи в виде

5₁₁+8₁₂+9₁₃+8₁₄+7₂₂+14₂₃  max,

-3₁₁-2₁₂+3₁₃+12₁₄ +3₂₂+12₂₃ 8,

₁₁ +2₁₂+3₁₃+4₁₄ 1,

₁₁ +2₁₂+3₁₃+4₁₄ 4,

₁₁ +₁₂+₁₃+₁₄=1,

₂₁ +₂₂+₂₃=1,

_jk 0.

Эта задача решается любым универсальным методом ЛП без добавления правила ограниченного ввода.

-постановка

Построение аппроксимирующей задачи основано так же на кусочно-линейном приближении, но меняется уравнение сетки. По узлам сетки вычисляются расстояния между смежными узлами (длины интервалов)

_jk = X_jk+1 – X_jk

и уравнение сетки записывается в виде

x_j = d_j + ; (8.25)

0  y_jk  1, (8.26)

где y_jk – новые переменные.

Из представления переменной в виде (8.25), (8.26) следует:

• x_j = d_j, когда  y_jk =0;

• x_j находится в первом интервале, когда y_j1  (0, 1), остальные y_jk=0;

• x_j находится во втором интервале, когда y_j1=1, y_j2  (0, 1), остальные  y_jk=0;

• x_j находится в k-ом интервале, когда y_j1 = y_j2 = ... = y_jk-1 = 1, 0  y_jk  1,

остальные y_jk=0.

Таким образом, для правильной аппроксимации должно выполняться установленное соответствие между значениями переменной x_j и y_jk. Это требование аналогично правилу смежных весов. При ином представлении значения x_j будет нарушена кусочно-линейная аппроксимация функции.

Для аппроксимации нелинейной составляющей функции критерия вычисляются разности ее значений в смежных узлах

_jk = f_j (X_jk+1) – f_j (X_jk),

с помощью которых записывается аппрокимирующая функция

(8.27)

Тогда функция, аппроксимирующая критерий, имеет вид

Аналогично аппроксимируются ограничения _ij(x_j):

Как и в -постановке, если имеет место задача выпуклого программирования, то требования к переменным y_jk выполняются автоматически и полученное решение будет приближенным глобальным решением исходной задачи. В противном случае, необходимо придерживаться правила ограниченного ввода относительно переменных y_jk: если первые k переменных равны единице, вводить можно только y_jk+1.

При практическом решении сепарабельных задач сначала можно взять малое число узлов и получить приближенное оптимальное решение. Затем в качестве исходных принять интервалы, на которых лежат оптимальные x_j, и выполнить аппроксимацию функций только на этих интервалах с малыми расстояниями между узлами. Такой способ снижает размерность решаемых задач и повышает точность получаемого решения.

Следует заметить, что в ряде случаев несепарабельная функция может быть преобразована к сепарабельной. Способ преобразования зависит от структуры функции. Например, произведение двух сепарабельных функций S(X)T(X) можно привести к сепарабельному виду, заменив его перменной v с дополнительными равенствами

S(X) = z – y; T(X) = z + y.

Тогда v = (z - y)(z + y) = z² – y² – сепарабельная функция. Так функция

f = x₁ + x₂x₃² заменяется на сепарабельную f = x₁ + v с дополнительными сепарабельными ограничениями

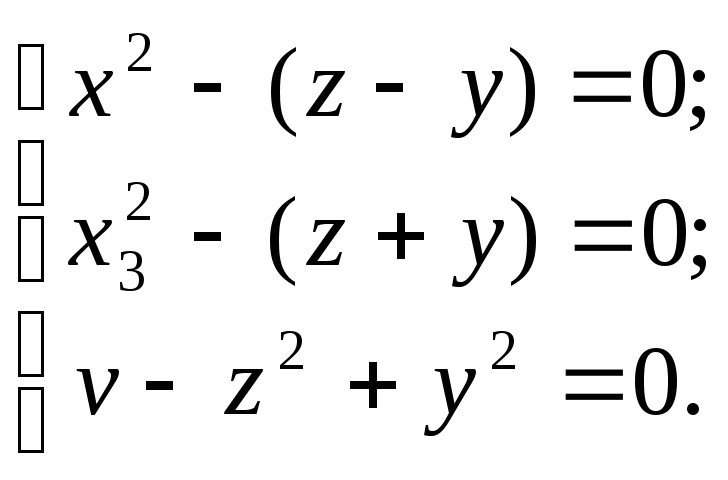
Пример 8.4.Покажем, что некоторые стохастические задачи могут сводиться к сепарабельным. Стохастические модели описывают ситуации выбора решения в условиях риска, обусловленного влиянием случайных факторов. Предполагается, что закон распределения случайных величин известен.

Пусть зависимости от искомых переменных линейны, но коэффициенты критерия и ограничений зависят от случайной величины (состояния среды). В этом случае в качестве критерия берется обычно математическое ожидание линейной формыM(L)=M[C^T()X]=а запись ограничений зависит от требований к их выполнению. При допустимости некоторых нарушений условий задачи ограничения записываются в вероятностной форме:

где p_i- заданное значение вероятности. выполнения i-го условия. Такое ограничение заменяется эквивалентным детерминированным условием

(*)

где - математические ожидания, - дисперсия , -дисперсия , =t(p_i) – значение функции, обратной функции распределения (например, нормального).

В результате детерминированная модель стохастической задачи включает линейный критерий и существенно нелинейные ограничения (*). Очевидно, что она не является сепарабельной. Сделаем простое преобразование. Обозначим

.

Тогда каждое ограничение (*) заменяется двумя условиями:

Первое из них – линейное, а второе – сепарабельное. Таким образом, стохастическая задача приведена к сепарабельной.

Примечание. Если случайным является только вектор ограничений, то, как следует из (*), стохастическая задача сводится к линейной.