9.3. Машина Тьюринга

Машина Тьюринга - одна из моделей алгоритмов названа в честь английского математика Алана Тьюринга (1912-1954).

Машина Тьюринга включает: 1) управляющее устройство, которое может находиться в одном из состояний, образующих конечное множество Y={y₁,y₂,...,y_k}; 2) ленту, разбитую на ячейки, в каждой из которых может быть записан одни из символов конечного алфавита Х={х₁,х₂,...,х_p}; 3) устройство обращения к ленте - считывающую и записывающую головку, которая в каждый момент времени "обозревает" ячейку, в зависимости от символа в ячейке и состояния управляющего устройства записывает в эту ячейку новый символ (он может совпадать с прежним, считываемым) или пустой, т.е. символ стирается и записывается символ пробела. Далее устройство обращения сдвигается на ячейку влево или вправо или остается на месте. При этом управляющее устройство переходит в новое внутреннее состояние или остается в старом (текущем). Среди состояний устройства управления выделяются начальноеy₁и заключительное y_kсостояния (k- мнемонический знак окончания работы). В начальном состоянии машина Тьюринга находится перед началом работы, в конечном - машина останавливается после окончания работы.

Память машины Тьюринга - конечное множество состояний (внутренняя память) и лента (внешняя память). Лента бесконечна в обе стороны, однако в начальный момент времени только конечное число ленты заполнено символами, остальные пусты, т.е. содержат пустой символ - символ пробела .

Данные машины Тьюринга - слова в алфавите ленты, на ленте записываются исходные данные и затем - результат.

Элементарные шаги - это считывание и запись символов, сдвиг головки, переход устройства управления из состояния в состояние.

На рис.9.2 изображена структурная схема машины Тьюринга. Под воздействием входного символа х, например I, считываемого головкой, устройство управления формирует выходной символZ, управляет движением головки: влево (L), вправо (R) или на месте (Е).



1

Рис.9.2. Структурная схема машины Тьюринга

Полное состояние машины, или конфигурация (или машинное слово), по которому однозначно определяется ее дальнейшее поведение, описывается ее внутренним состоянием y_i, символами слева и справа от головки, например: ...x₁y_ix₂... Система команд машины содержит записи вида, где х₁- читаемый символ в состоянииy₁;y₂- новое внутреннее состояние;- записываемый символ;R- признак продвижения головки,- символ перехода машины в новое состояние (не путать с импликацией!).

Совокупность всех команд называется программой. Каждая машина Тьюринга определяется своим алфавитом, состояниями внутренней памяти и программой.

Чтобы полностью определить работу машины, надо указать ее конфигурацию для начального момента времени. Будем считать, что в начальной конфигурации головка воспринимает самую левую непустую ячейку.

Итак, машина Тьюринга есть, по определению тройка

М = <X,Y,П>,

где Х - алфавит символов ленты с выделенным пустым символом (пробелом);Y- алфавит внутренних состояний с выделенными символами начального состоянияy₁и конечногоy_k; П - программа, т.е. конечная последовательность упорядоченных пятерок символов - команд.

Если машина, начав работу с некоторым словом, записанным на ленте, придет в заключительное состояние, то она называется применимойк этому слову. Результатом ее работы считается слово, записанное на ленте в заключительном состоянии. Если же машина ни в какой момент времени не придет в заключительное состояние, то она называетсяне применимойк данному слову и результат ее работы не определен.

Пример 1: Рассмотрим машину Тьюринга, алфавит ленты которой содержит кроме символов пробела символ 1. Будем представлять некоторое число "а" в виде а символов 1, например,111- число 3,11111- число 5. Машина, увеличивающая записанное число на единицу, реализуется следующей программой:

;

;

;

.

Работа машины может быть описана графом переходов (рис.9.3), в котором дуги помечены условиями переходов (числитель), записываемыми символами и указанием направления движения головки (знаменатель).

Рис.9.3. Граф переходов машины Тьюринга,

реализующий алгоритм увеличения числа на единицу

Последовательность работы машины, например, для слова 11, описывается рисунком 9.4. Вначале головки находится у начала числа и по окончании работы должна установиться там же - у начала числа, увеличенного на 1.





1

1







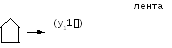
1

1





1

1







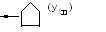
1

1

1





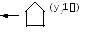
1

1

1





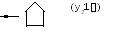
1

1

1





1

1

1



Рис.9.4. Последовательность работы машины Тьюринга,

реализующей алгоритм увеличения числа на единицу

Такая машина применима к любому слову в алфавите {,1}.

Работа машины Тьюринга может быть описана таблицей (табл.9.1).

Табл.9.1

Внутреннее	Символ
состояние		1
y1
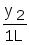
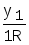
y2
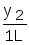
yk

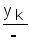
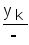
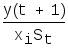
Строку с y_kможно опустить. В табл.9.1x_i- выходной символ,S_t{L,R,E}.

Пример 2: Рассмотрим пример реализации алгоритма сложения чисел а и в, записанных на ленте в виде а и в единиц с разделителем . Обозначим такую запись 1^а, 1^в. Следовательно, необходимо переработать слово 1^а1^вв слово 1^а+в, т.е. удалить разделительный символи сдвинуть одно из слагаемых, скажем, первое ко второму (как на счетах).

Такой алгоритм осуществляет машина Тьюринга, граф переходов устройства управления которой изображен на рис.9.5. Здесь в числителе - считываемый символ, в знаменателе - записываемый символ и знак управления движением головки.

Рис.9.5. Граф переходов машины Тьюринга,

реализующей алгоритм сложения двух чисел,

заданный единицами

Пусть, например, заданы числа 1²и 1¹. Тогда последовательность работы машины может быть описана рис.9.6. В исходном головка установлена напротив начала первого числа (напротив первой его единицы). Головка на месте первой единицы записывает пробели движется до разделителя, найдя который, записывает вместо него 1 и начинает движение влево, останавливается напротив первого пробела, а затем сдвигается вправо к первой единице.

На графе рис.9.5 переход необходим для случая отсутствия первого числа, т.е. когда исходное слово имеет вид1^в.

1²1¹



1

1



1







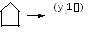
1



1

1





1



1







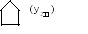
1

1

1







1

1

1







1

1

1



1³





1

1

1



Рис.9.6. Последовательность работы машины Тьюринга,

реализующей сложение чисел 1²(11) и 1¹(1)

Тогда система команд имеет вид:

Аналогично могут быть построены некоторые другие простые машины Тьюринга, в том числе машина для разветвления алгоритма, организации цикла и т.д. Из простых машин Тьюринга можно простроить более сложные путем композиции. Пусть М₁и М₂- две машины Тьюринга с общим алфавитом{x₁,x₂,...x_n}, а{y_k,y₁,...y_m}- внутреннее состояние первой машины,{y_k,,...}- внутреннее состояние второй машины.

КомпозициейМ машины М₁и М₂называется машина с алфавитом{x₁,x₂,...x_n}, внутренними состояниями{y_k,y₁,...y_m,y_m+1,...y_m+l}и программой, получаемой следующим образом. Во всех командах М₁заменяется заключительный символ состоянияy_kна символy_m+1, а остальные символы остаются без изменения. Во всех командах машины М₂символy_kоставим неизменяемым, а остальные символы(i=1,...l) заменяются соответственно символамиy_m+i. Совокупность всех команд машин М₁и М₂, измененная указанным образом, и будет программой композиции М машин М₁и М₂. "Работа" машины М равносильна последовательной "работе" машин М₁и М₂. Можно "сконструировать" и универсальную машину Тьюринга, которая, в отличие от рассмотренных, "читает" любую программу, записанную на ленте и выполняет ее по аналогии с современными ЭВМ. То есть устройство управления выполняет не одну какую-то программу, а любую программу, записанную на ленте (данные также записаны на ленте). А.Тьюринг выдвинул следующую гипотезу.

Тезис Тьюринга. Всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга. Как показывает опыт, любые действия, которые может выполнить вычислитель-человек, могут быть представлены последовательностью действий некоторой машины Тьюринга.

Часто в алгоритмических проблемах идет речь о вычислимости некоторых специальным образом построенных функций.

Частичная числовая nместная функцияf(x­₁,...x_n)называетсявычислимой по Тьюрингу, если существует машина, вычисляющая ее в следующем смысле:

1. Если набор значений аргументов принадлежит области определения функции f, то машина, начав работу в некоторой конфигурации, задающей значение аргументов, останавливается, заканчивая работу в конфигурации, соответствующей значению функции.

2. Если набор значений аргументов не принадлежит области определения функций f, то машина, начав работу в некоторой конфигурации, работает бесконечно, не приходя в заключительное состояние.

Программу машины Тьюринга можно закодировать следующим образом. Представим в общем виде команду:

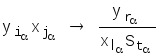,=1...k,

где k- число программ (машин),

S₁- этоR,S₂=R, S₃=E.

Можно считать, что существуют некоторые обширные алфавиты X₀ и Y₀, в которых записываются символы для всех машин Тьюринга, тогда символыy_i, x_j, y_r, x_l - символы этих алфавитов.

Один из способов нумерации всех машин Тьюринга предложил Гедель.

Пусть р₁,р₂,р₃... последовательность всех простых чисел, расположенных в порядке возрастания (т.е. последовательность 2,3,5,7,11...). Номером машины Тьюринга М с программойnназовем число

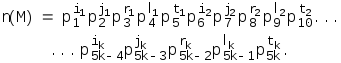
Закодируем, например, машину Тьюринга М₁с программой

Здесь алфавит X₀={1,}, Y₀={y₁,y_k}, кроме тогоt={1,2,3}соответствуетL,R,E.

Таким образом,

n(М₁)=

Естественно, не все натуральные числа являются номерами машин Тьюринга. Если n- номер некоторой машины, то ее программу можно однозначно установить по этому номеру.