
9.2. Рекурсивные функции
Будем рассматривать только числовые функции, т.е. функции, аргументы и значения которых принадлежат множеству натуральных чиселN=0,1,2... Числовая функция, значение которой можно вычислить посредством некоторого единого алгоритма, называетсявычислимой.
Если имеется алгоритм, следуя которому можно по известным значениям аргумента найти значение функции, называется эффективно вычислимой.
Частичная числоваяn-местная функцияf(x1,...xn)определена на некотором подмножестве МNn с натуральными значениями. Если область определения совпадает с множествомNn, т.е.f: Nn N, гдесимвол отображения, то говорят, что функцияNвсюду определенная, иначе - частично определенная. Например,f(x1,x2) = x1+x2- всюду определенная двухместная функция,f(x1,x2) = x1-x2- частично определенная функция, определенная при х1х2. Рекурсивным заданием функции принято называть такое ее задание, при котором значение функции для данных аргументов определяется значениями той же функции для более простых аргументов или же значениями более простых функций. Простейшим примером рекурсивного определения являются числа Фиббоначи, представляющие собой последовательность чиселf(n), удовлетворяющих условиямf(0)=1, f(1)=1, f(n+2)=f(n)+f(n+1), т.е. 1,1,2,3,5,8,13...
Опишем класс числовых функций, играющих весьма важную роль в теории алгоритмов. Следующие всюду определенные числовые функции назовем простейшими:
1) S(x)=x+1- функция следования;
2) 0(х)=0 - константа нуля;
3) Im(x1,...xn)=xm, m=1...,n- проектирующая функция, выбирающаяm-й аргумент изnаргументов.
Все эти функции вычислимы в интуитивном смысле.
Определим теперь средства получения новых функций (операции или оператора). Они обладают тем свойством, что, применяя их к функциям, вычислимым в интуитивном смысле, получаем функции, также вычислимые в интуитивном смысле.
1. Операция суперпозиции. Говорят, чтоn-местная функция(х1,хn) получена с помощью оператора суперпозиции изm-местной функции(х1,хm) иn-местных функций от одних и тех же переменныхf1(х1,хn),...,fm(х1,хn), если
(х1,...,хn)=(f(х1,...,хn),...,fm(x1,...,xn)).
Значение функции определено, если определеныf1...fm и(f1...fm).
Пусть, например, f1(x,y)=x-y,
f2(x,z)=x2+z,![]() .
Мы рассматриваем функции от натурального
аргумента, принимающие натуральные
значения, поэтому значения указанных
функций будем считать определенными
лишь в случае, когда они целые и
неотрицательные. Суперпозиция функцийиf1,f2
записывается в виде
.
Мы рассматриваем функции от натурального
аргумента, принимающие натуральные
значения, поэтому значения указанных
функций будем считать определенными
лишь в случае, когда они целые и
неотрицательные. Суперпозиция функцийиf1,f2
записывается в виде
![]() .
.
Таким образом, получена трехместная функция из двухместных. Таким же образом возможна суперпозиция при наличии одной логической функции:
![]()
![]() .
.
Получена трехместная логическая функция из двух одинаковых двухместных логических функций.
2. Операция примитивной рекурсии. Говорят, что (n+1) местная функцияf(x1,...xn,g)получена изn-местной функции(х1,хn) иn+2 местной функции(х1,...,хn,y,z) с помощью оператора примитивной рекурсии, если ее значения можно вычислить по следующей схеме, которая называется схемой примитивной рекурсии:
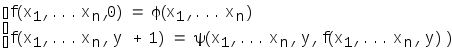
При n=1 схема примитивной рекурсии имеет вид
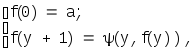
где а - константа.
Здесь y+1 последующее значение,y- текущее значение.
Эти уравнения позволяют последовательно находить значения f(0)=a, f(1)=(0,f(0)),f(2)=(1,f(1)), f(3)=(2,f(2)),.., и, следовательно, полностью задают функциюf.
В качестве примера рассмотрим функцию, определяемую соотношением
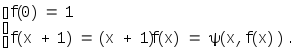
Для нее f(0)=1, f(1)=1f(0), f(2)=2f(1)=21=2, f(3)=3f(2)= =32=6и т.д. Легко видеть, чтоf(x)=x!
Функция от двух аргументов может быть задана условиями:
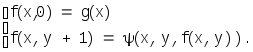
Здесь первый аргумент является параметром, а рекурсия ведется по второму аргументу. Так, например, функция f(x,y)=xyопределяется соотношениями
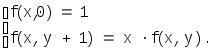
Это следует из того, что х0=1,xy+1=ххy.
Функция f(x1,...xn) называется примитивно-рекурсивной, если она может быть получена из простейших функций с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.
Примеры примитивно-рекурсивных функций:
а) функции S(x), 0(x), Im(х1,х2...хn);
б) функции-константы 1=S(0(х)), 2=S(S(0(х)))и т.д.;
в) функция 0(х1,...хn)=0, так как 0(х1,...хn)=0(I1(х1...хn)) = 0(х)=0, т.е. получена из простейших функций 0(х),I1(х1...хn) с помощью оператора суперпозиции;
г) f(x)=x+n, т.е.f(x)=S(S(...S(x))...);
д) f(x,y)=x+y, действительно,
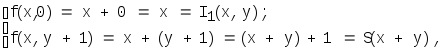
т.е. f(x,y)=x+yполучена из примитивно-рекурсивный функций(х)=I1(х) и(x,y,z)=z+1=S(z)с помощью оператора примитивной рекурсии. Аналогично может быть доказана примитивная рекурсивность умножения, возведенные в степень и т.д.
Определим функцию x-y(арифметическое или "урезанное" вычитание):
x
0 в противном случае.![]() y=
y=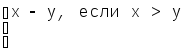
Тогда примитивно-рекурсивным следующие функции:
1) f(x)=x![]() -1:
-1:
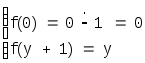
2) f(x,y)=x![]() y:
y:
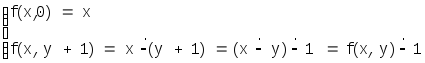
Пользуясь последней функцией определим функции
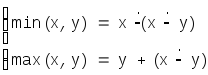
Зададим как примитивно-рекурсивные "арифметизованные" логические функции, т.е. числовые функции, которые на множестве {0,1}ведут себя как логические:
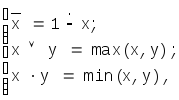
где х,y{0,1}.
Из функциональной полноты этого множества функций и того, что суперпозиция является примитивно-рекурсивным оператором, следует примитивная рекурсивность всех логических функций.
3. Оператор минимизации (- оператор). Говорят, что функцияf1(x1,...xn)получена из функцииg(x1,...xn,y)с помощью оператора минимизации (или просто-оператора) и обозначаютf(x1,...xn)=y[g(x1,...xn,y)=0], еслиf(x1,...xn)определена и равнаyтогда и только тогда, когдаg(x1,...xn,0),..., g(x1,...xn,y-1)определены и не равны 0, аg(x1,...xn,y)=0.
Пусть, например, имеется n-местная частичная функцияg(x1,...xn-1,y). Фиксируем некоторый набор (x1,...xn) и рассмотрим уравнение относительноy:
g(x1,...xn-1,y)=xn.
Будем решать это уравнение, последовательно вычисляя g(x1,...xn-1,0),g(x1,...xn-1,1),g(x1,...xn-1,2)... Наименьшееg, для которого окажетсяg(x1,...xn-1,y)=xn, и обозначаютg(g(x1,...xn-1,y)=n).
Считается, что это значение не определено, если в процессе последовательного вычисления встретилось некоторое g0, при которомg(x1,...xn-1,g0)не определено (в частности, это может быть приg0=0), а при всех меньшихgуравнение не выполняется, либо еслиg(x1,...xn-1,g)определено при всехg, но отлично отxn. Значениеg(g(x1,...xn-1,y)=xn) является функцией переменныхx1,...xn. Говорят, что функция
f(x1,...xn)=g(g(x1,...xn-1,y)=xn)
получена из функции gоперацией минимизации.
В качестве примера рассмотрим функции
f(x1,x2)=g(y-x1=x2).
При х1=0 минимальным из значенийy=0,1,2.., удовлетворяющих уравнениеy-х1=х2, является х2. Если же х11, то в процессе отыскания минимального решения переборомy=0,1,2... мы наткнемся на неопределенное значение уже приy=0 (ибо 0-х1<0). Таким образом,
f
Не определено в остальных случаях.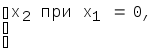
Типичной ситуацией применения операции минимизации является построение обратной функции. Используя, например, функции x+y, xy, x2и т.д., можно получить обратные от функции:
x-y=z(x+z=y),
![]() =z(xy=z),
=z(xy=z),
![]() =y(y2=x)и т.д.
=y(y2=x)и т.д.
Функции x-y,![]() и
и![]() являются частичными. Следовательно,
операция минимизации даже в применении
к всюду определенным функциям может
давать частичные функции.
являются частичными. Следовательно,
операция минимизации даже в применении
к всюду определенным функциям может
давать частичные функции.
Функция f(x1,...xn)называется частично рекурсивной, если она может быть получена из простейших функций с помощью конечного числа применения операторов суперпозиции, примитивной рекурсии и минимизации. Всюду определенные частично рекурсивные функции еще называются общерекурсивными.
Говорят, что функция f(x)получается из функцииg(x)с помощьюитерациии обозначаютf(x)=ig(x), если

Говорят, что функция f(x)получается из функцииg(x)с помощьюобращенияи обозначаютf(x)=g-1(x), если
f(x)=y[g(y)=x].
Абстрактная схемная интерпретация примитивной рекурсии представлена рис.9.1.
Схема состоит из устройства, вычисляющего функцию hот двух переменных и задержки на один такт (шаг). По (линиям) каналам схемы передаются натуральные числа. Времяtбудем считать дискретным:t=0,1,2... Оно описывает шаги вычисления. Выходfзависит не только от х, но и от момента времени, т.е. представляет собой функциюf(x,t).

Рис.9.1. Схемная интерпретация примитивной рекурсии
В начальный момент t=0 значение второго входа вычислителяhявляется константой с, зависящей от начального состояния схемы:f(x,0)=h(x,c)=g(x).
В момент t=1f(x,1)=h(x,f(x,0)); в общем случаеf(x,t+1)= =h(x,f(x,t)). Таким образом, схема рис.9.1 реализует примитивную рекурсию по переменнойt, т.е. по времени. Если, например,hвыполняет умножение, а с=1, тоf(x,t)=xt+1.
Все ли функции являются примитивно-рекурсивными? Можно показать, что множество всех одноместных целочисленных функций типа N N, гдеN- множество натуральных чисел, несчетно, тем более это верно для функций типаNn N. Каждая примитивно-рекурсивная функция имеет конечное описание, т.е. задается конечным словом в некотором фиксированном для всех функций алфавите. Множество всех конечных слов счетно, поэтому примитивно-рекурсивные функции образуют не более чем счетное подмножество несчетного множества функций типаNn N.
Более того, не все вычислимые функции можно описать как примитивно-рекурсивные. Например, для так называемой функции Аккермана, вычислению в точке (3,3) должно предшествовать вычисление в точке (2,4), вычислению в точке (3,4) должно предшествовать вычисление в точке (2,16). Здесь ведется двойная рекурсия и по х и по y, т.е. двойная рекурсия не всегда сводится к примитивной рекурсии.
Функция Аккермана - пример вычислимой, но не примитивно-рекурсивной функции. Операторы кратной рекурсии не дают замыкания класса всех вычислимых функций: для любого nнайдется функция, определимая с помощьюn-кратной рекурсии (n-рекурсивная), но не (n-1) рекурсивная. Для расширения средств построения вычислимых функций вводится неограниченный-оператор.
В теории алгоритмов доказывается, что всякая функция, вычислимая некоторым алгоритмом, частично рекурсивна.
