8.3.3. Исчисление предикатов

Итак, в логике предикатов, в отличие от логики высказываний, нет эффективного способа распознавания общезначимости формул. Поэтому аксиоматический метод становится существенным при изучении формул с кванторами.

Рассмотрим исчисление предикатов, как узкую аксиоматическую теорию, алфавит и определение формул которой совпадает с алфавитом логики предикатов, за исключением того, что в качестве логических операций используем только операции ®, -.

Аксиомы исчисления предикатов, в качестве трех первых которых возьмем аксиомы исчисления высказываний:

А1. А®(В®А);

А2. (А®(В®С))®((А®В)®(А®С));

А3. (®)®((®А)®В).

А4. "x_i A(x_i) ® A(x_j), где формулаA(x_i)не содержит переменнойx_j.

А5. A(x_i)®$x_j A(x_j), где формулаA(x_i)не содержит переменнойx_j.

Как и ранее А1-А5 - тождественно истинные (общезначимые) формулы.

Правила вывода:

1. Правило m.p:.

2. Правило связывания квантором общности:

,

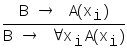где формула В не содержит переменной x_i.

3. Правило связывания квантором существования:

,

где формула В не содержит переменной x_i.

4. Правило переименования связанной переменной.

Связанную переменную формулы А можно заменить (в кванторе и во всех вхождениях в области действия квантора) другой переменной, не являющейся свободной в А.

Докажем общезначимость формулы

$x_i"x_j A(x_ix_j) ® "x_j $x_i A(x_ix_j).

1. Ã"x_j A(x_ix_j) ® A(x_ix_t)По аксиоме 4.

2. Ã A(x_ix_t)®$x_k A(x_kx_t)По аксиоме 5.

3. à А®В, В®Сà А®С по теореме дедукции, которая доказывается отдельно:

(ÚВ)(ÚС)®(ÚС)

АÚВÚÚС =ÚВÚÚС = 1.

4. Ã"x_j A(x_ix_j) ®$x_k A(x_kx_t), где 3 применено к 1 и к 2.

5. Ã$x_i"x_j A(x_ix_j) ®$x_k A(x_kx_t)- по правилу вывода 3 из 4) - связывание квантором существования.

6. Ã$x_i"x_j A(x_ix_j) ®"x_t$x_k A(x_kx_t)- правило вывода 2 из 5.

7. Ã$x_i"x_j A(x_ix_j) ®"x_j $x_k A(x_kx_j)- правило вывода 4 из 6: переименованиеx_t вx_j.

8. Ã$x_i"x_j A(x_ix_j) ®"x_j $x_i A(x_ix_j)- правило вывода 4 из 7: переименованиеx_k в x_i.

В математической логике доказывается, что исчисление предикатов непротиворечиво - то есть в нем невозможно одновременно вывести А(ÃА), и(Ã). Кроме того, в силу теоремы Геделя о полноте исчисления предикатов общезначимая формула выводима в исчислении предикатов.

Рассмотренное исчисление предикатов - исчисление предикатов первого порядка. В исчислениях второго порядка возможны кванторы по предикатам, т.е. выражение вида "Р(Р(х)).

Итак, множество всех истинных высказываний логики высказываний перечислимо и разрешимо. Множество всех истинных высказываний логики предикатов перечислимо (ввиду его полноты), но неразрешимо (ввиду бесконечности предметной области).

В приложении 1 представлен дополнительный материал по общей логике.

В математической логике рассматривается в качестве еще одной формальной теории так называемая формальная арифметика.

Гедель доказал, что любая формальная теория Т, содержащая формальную арифметику, неполна: в ней существует замкнутая формула F, такая, чтоистинно, но ниF, нине выводимы в Т. В соответствии со знаменитой теоремой Геделя о неполноте, для любой непротиворечивой формальной теории Т, содержащей формальную арифметику, формула, выражающая непротиворечивость Т, недоказуема в Т.

Таким образом, арифметика и теория чисел являются неаксиматизируемыми теориями.

Таким образом, множество всех истинных высказываний арифметики неперечислимо.

Теоремы Геделя имеют важное методологическое значение. Оказывается, для достаточно богатых математических теорий не существует адекватных формализаций. Правда, любую неполную теорию Т можно расширить, добавив к ней в качестве аксиомы истинную, но не выводимую в Т формулу, однако, новая теория также будет неполна. Кроме того, невозможно исследовать метасвойства теории средствами самой формальной теории, т.е. всякая метатеория Т для того, чтобы иметь возможность доказывать хотя бы непротиворечивость, должна быть богаче Т.

Таким образом, под сомнение берется сам подход построения математики как некоторой фиксированной совокупности средств, которые можно было бы объявить единственно законными и с их помощью строить метатеории любых теорий. Но это вовсе не крах формального подхода. Наличие неразрешимых проблем не говорит о том, что конструктивный подход не пригоден, если он чего-то и не может, то лишь потому, что этого не может никто.

Невозможность полной формализации содержательно определенных теорий - это не недостаток концепции, а объективный факт, неустранимый никакой концепцией.

Невозможность адекватной формализации теории означает, что надо либо искать формализуемые ее фрагменты, либо строить более сильную формальную теорию, которая, правда, снова будет неполна, но, быть может, будет содержать всю исходную теорию.

В дальнейшем мы рассмотрим некоторые другие примеры абстрактных формальных систем.