Часть 2: векторы и действия над ними Лекция 8

Замена базиса и скалярное произведение векторов

Напомним (см. пример 9), что если в пространстве зафиксирован естественный базис, то для любых векторовсправедливы соотношения:

=.

(32)

Введем в рассмотрение новый ортонормированный базис . В соответствии с формулой (19) имеем:=, причем по теореме 12 матрицаSортогональна. Разлагая векторыиотносительно нового базиса, получаем точно так же, как в (21):

,

.

(33)

Применяя равенства (33) и свойства скалярного произведения векторов, получаем:

=.

В силу ортонормируемости базиса (см. определение 22) получаем, что приk=i, а при. Поэтому

.

Вспоминая определение 17 скалярного произведения векторов, делаем заключение, что мы доказали следующую теорему:

Теорема 13.При замене ортонормированного базиса на какой-либо другой ортонормированный базис скалярное произведение векторов не изменяет своего значения.



Проиллюстрируем доказанную теорему следующим рисунком:

Так как в силу определения 18 норма вектора и угол между векторами выражаются через скалярное произведение векторов, то и норма, и угол не изменяются при замене исходного ортонормированного базиса на новый ортонормированный базис. То же касается и проекции вектора на вектор (см. определение 19).

Векторное произведение векторов в

Определение 24.Векторным произведением векторовиназывается вектор, обозначаемыйи вычисляемый по формуле:

	.	(34)
			

Заметим, что в первом столбце определителя, входящего в равенство (34), стоят не числа, а векторы. Однако и определение определителя, и его основные свойства сохраняются. Например, из свойства 1 теории определителей вытекает, что

.

(35)

В таком виде формула для вычисления векторного произведения часто встречается в литературе. Если применять формулу (34), то определитель следует раскладывать по первому столбцу, а в случае (35) лучше применять разложение по первой строке.

Числовая иллюстрация.Пусть,. Используя (34), имеем:

.



Свойства векторного произведения

1. (антикоммутативность);

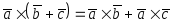2. (дистрибутивность);

3. (ассоциативность по отношению к умножению на число);

4. тогда и только тогда, когда векторыилинейно зависимы.

Доказательство.Антикоммутативность вытекает из свойства 2 определителей, примененного к столбцам, а дистрибутивность и ассоциативность – соответственно из свойств 5 и 4 теории определителей. Докажем последнее предложение.

Если илинейно зависимы, то по свойству 1 систем векторов один из этих векторов выражается через другой, умноженный на число. Пусть, например,. Тогда, применяя последовательно свойства 4 и 3 теории определителей, получаем:

=.

Обратное утверждение можно получить из результатов теоремы 15.



Заметим, что из формулы (34) непосредственно следует правило векторного умножения базисных векторов и:. Если мы заменим базисновым ортонормированным базисом, то можно доказать следующую лемму:

Лемма 5.ЕслиS– матрица перехода от базисак базису, то

,

,

.

(36)

Доказательствопроводится прямым вычислением по формуле (34) с использованием соотношений, следующих из равенства, гдевычисляется по формуле (12). Рекомендуем читателю проделать необходимые выкладки.



Применяя теорему 11, мы видим, что для нашей ортогональной матрицы Sвозможны два варианта: либо, либо. Можно доказать, что первый случай соответствует возможности повернуть базисную тройкувокруг точки приложения этих векторов до совпадения с тройкой. Из рисунка ясно: вращая тройку

вокруг точки приложения векторов и совместив при этом векторс вектором, а векторс вектором, получим, что векторсовместится с вектором. В двумерном случае поворот базисабыл изучен в примере 15. Из полученной там формулы (28) следовало, что. Вариантсоответствует случаю, когда с помощью поворота тройку векторовнельзя совместить с новой тройкой(см. рисунок ниже).

В соответствии с вышесказанным естественно ввести следующее

Определение 25.Ортогональная матрицаSназывается матрицей поворота ортонормированного базиса, если.

ٱ

Теорема 14.Пусть вектораите же, что и в определении 24, и пусть их разложения относительно нового базисаимеют вид:и. Тогда

.

В частности, если S– матрица поворота, то векторное произведение, вычисленное в координатах относительно естественного базиса (см. определение 24) совпадает с векторным произведением тех же векторов, вычисленным относительно нового базиса:

.

(37)

Доказательство.Используя свойства векторного произведения, имеем:

+.

Применяя теперь равенства (36), получаем:

=.



Следующая теорема проясняет геометрический смысл векторного произведения.

Теорема 15.Векторное произведениеесть вектор, удовлетворяющий следующим условиям:

1. норма этого вектора равна площади параллелограмма, построенного на векторах икак на сторонах;

2. вектор ортогонален и вектору, и вектору;

3. направление вектора определяется по правилу буравчика: если лезвие буравчика установить перпендикулярно плоскости, в которой лежат вектораи, а ручку буравчика вращать от векторак векторув сторону наименьшего угла между этими векторами, то направление векторасовпадет с направлением движения лезвия буравчика.

Доказательство.Вместо естественного базисапостроим новый ортонормированный базистак, как показано на рисунке. Именно, приведем все векторы к одному началу, направим векторпо вектору, векторрасположим на плоскости, содержащей вектораи, а векторнаправим с таким расчетом, чтобы тройкаполучалась поворотом тройки. Тогда,+ +. По построению базисаполучаем. По формуле (37):

.

(38)

Ясно, что , где последнее равенство – это элементарная геометрическая формула для вычисления площади параллелограмма, натянутого на вектораи. Так какортогоналени, то по построениюортогонален векторамии, следовательно,ортогонален векторами. Поскольку направление вектора, очевидно, определяется по векторамис помощью правила буравчика, а тройкаполучилась из тройкиповоротом, то и направление вектора(см. лемму 5) определяется по векторамис помощью правила буравчика. Вид коэффициента прив формуле (38) говорит о том, что иопределяется по векторамис помощью правила буравчика.