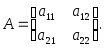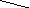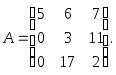МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании кафедры высшей математики 11.06.2011 г.

Линейная алгебра и аналитическая геометрия

Раздел 1. Линейная алгебра

Курс лекций

и образец решения индивидуального задания

по высшей математике для бакалавров 1-го курса

очной формы обучения

Ростов-на-Дону

2011

УДК 517(07)

Линейная алгебра и аналитическая геометрия. Раздел 1. Линейная алгебра. Курс лекций и образец решения индивидуального задания по высшей математике для бакалавров 1-го курса очной формы обучения. – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 50 с.

Изложен курс лекций по линейной алгебре. Приведен образец индивидуального задания, снабженный подробным решением входящих в него задач.

Лекции 1-9 составлены И.В. Павловым. Образец решения индивидуального задания составлен М.М. Цвиль и адаптирован к курсу лекций И.В.Павловым.

Предназначены для бакалавров 1-го курса очной формы, проходящих обучение на кафедре высшей математики РГСУ, а также на математических кафедрах других вузов.

Электронная версия находится в библиотеке, ауд. 224.

УДК 517(07)

Составители:	д-р физ.-мат.наук, проф. И.В. Павлов канд. физ.-мат.наук, доц. Цвиль М.М.
Рецензенты:	канд. физ.-мат.наук, доц. А.М. Можаев канд. физ.-мат.наук, доц. Г.А. Власков

Редактор Т.М. Климчук

Доп. план 2011 г., поз. 176

Подписано в печать 12.07.11. Формат 6084/16. Бумага писчая. Ризограф.

Уч.-изд.л. 4,2. Тираж 50 экз. Заказ 378

Редакционно-издательский центр

Ростовского государственного строительного университета

344022, Ростов-на-Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2011

Часть 1: матрицы и определители Лекция 1

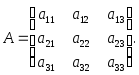
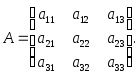
Определение 1.Квадратной матрицей порядкаn называется прямоугольная таблица, состоящая изn²чисел и имеющая вид:

		(1)
		ٱ

В элементематрицыAиндексi(соответственно, индексj) обозначает номер строки (соответственно, номер колонны), в которой находится этот элемент.

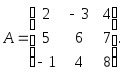
Числовая иллюстрация.Рассмотрим матрицу

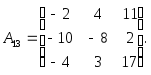
Здесь n=4; к примеру,Если из этой матрицы удалить первую строку и третью колонну, то получим следующую матрицу 3-го порядка:

		ٱ

Определение 2. 1) Определителем |A| матрицыAпервого порядка называется единственный элемент, из которого эта матрица состоит, т.е. для

2. Определителем матрицы Aпорядка 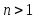называется число

(2)

где матрица порядка получается из матрицыAуничтожением первой строки иk-й колонны.

ٱ

Пример1.Пусть, т.е.

Согласно определению 2,

т.к. – матрицы первого порядка. Таким образом, получаем вычислительную формулу:

		(3)
		ٱ

Числовая иллюстрация.Пусть

Тогда

ٱ

Пример 2.Пусть, т.е.

Согласно определению 2,

=+Отсюда получаем геометрический способ вычисления определителя 3-го порядка:

	Соединенные отрезками элементы перемножаются и берутся со знаком +.	Соединенные отрезками элементы перемножаются и берутся со знаком –.

Однако на практике чаще всего применяется следующая вычислительная формула:

	.	(4)
		ٱ

Числовая иллюстрация.Пусть

Тогда

ٱ

Пример 3.Рассмотрим матрицуn-го порядка, у которой главная (т.е. наклоненная влево) диагональ состоит из единиц, а все остальные элементы которой равны нулю:

Такая матрица называется единичной. Имеем по формуле (2):

Следовательно,НоТаким образом,То есть, определитель единичной матрицы любого порядка равен единице.

ٱ

Заметим, что формулу (2), а также ее частные случаи (3) и (4), называют разложением определителя по первой строке.

Лемма 1.Для любой матрицыAвида (1) справедлива формула:

(5)

выражающая собой разложение определителя по первой колонне.

Доказательство.Доказательство проводится по индукции. Мы воспроизведем лишь три ее первых шага. Переход откnосуществляется аналогично, но его техническое оформление достаточно сложное.

При формула (5) дает:что совпадает с определением 2.

При 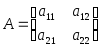. Используя формулу (3), имеем:

что совпадает с формулой (5).

При Используя геометрический способ вычисления определителя 3-го порядка (см. пример 2), получаем:

–что совпадает с формулой (5).

ٱ

Числовая иллюстрация.Пусть

Подсчет определителя данной матрицы разумнее вести разложением по первой колонне, так как в ней содержится много нулей. Имеем:

ٱ

Определение3.Поставим в соответствие матрицеA, заданной формулой (1), матрицу, чьи колонны совпадают с соответствующими строками матрицыA. Матрицаназывается транспонированной матрицей (по отношению кA).

ٱ

Числовая иллюстрация.

Е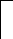сли, то.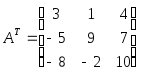

ٱ

Можно сказать, что получается вращением матрицыA вокруг ее главной диагонали. Обозначать матрицумы будем следующим образом:

(6)

Очевидно, что

Наряду с матрицей Aпорядкаnрассмотрим матрицыипорядка. Матрицаполучается транспонированием матрицыA, а затем удалением из полученной матрицыj-й строки иi-й колонны. Для конструирования матрицынужно сначала удалить изAi-ю строку иj-ю колонну, а затем транспонировать полученную матрицу.

Лемма 2.=.

Доказательство.Запишем матрицуAв виде:

.

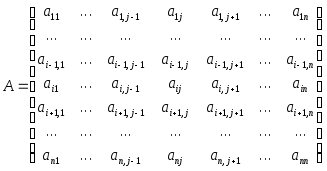
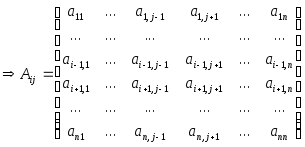
Аналогично,

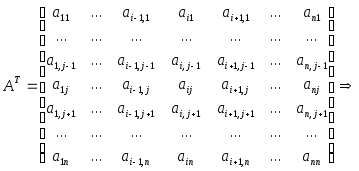
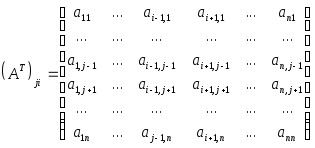. Лемма доказана.ٱ