Решение задачи 1.5

Так как , то обратная матрица существует (теорема 3 из лекции 4). Чтобы найти, нужно найти все алгебраические дополнения:

По формуле (12) из лекции 4 имеем:

⁼

(проверить самостоятельно соотношение

Система уравнений имеет единственное решение (см. первую часть доказательства теоремы 4 из лекции 4). Таким образом:

Решение задачи 2.1 Решим систему (остальные системы решаются аналогично).

В соответствие с правилом Крамера (см. теорему 4 из лекции 4) вычислим главный и вспомогательные определители данной системы:

В результате получаем:

Решение задачи 2.2

Метод Гаусса — это приведение системы к треугольному виду с помощью элементарных преобразований, производимых над строками системы. Эти преобразования таковы: перестановка уравнений системы; умножение уравнений системы на число, неравное нулю; сложение уравнений системы. Практически удобнее приводить к треугольному виду не саму систему уравнений, а матрицу из коэффициентов при неизвестных и свободных членов. Переход от одной матрицы к другой будем записывать при помощи знака равносильности ~, а строки будем символически обозначать буквой С с индексами (например, выражение означает, что мы ко второй строке прибавили первую, умноженную на число –3). Итак:

~ ~

~ _~

~ .

Таким образом, исходная система привелась к треугольному виду:

.

Из последнего уравнения получаем . Подставляя это значение в предыдущее уравнение, получаем. Подставляя иво второе уравнение, имеем:. И, наконец, подставляя,ив первое уравнение, находим

Решение задачи 3

Решить эту задачу самостоятельно, опираясь на заключительный раздел лекции 5.

Решение задачи 4

Имеем:

2+=2;

–=;

Решение задачи 5

Решение задачи 6

а) Воспользуемся критерием линейной независимости двух векторов в (см формулу (15) из лекции 5). Для этого составим определитель второго порядка из столбцов координат данных векторов:

.

Следовательно, векторы a и b линейно зависимы.

б) Проверим, пропорциональны ли соответствующие координаты векторов и. Не пропорциональны! Следовательно, ни один из векторовине может быть выражен через другой. По свойству 1 систем векторов (см. лекцию 5) данные векторы линейно независимы.

в) Согласно критерию линейной независимости трех векторов в R³ (опять см формулу (15) из лекции 5) составим определитель третьего порядка:

Следовательно, векторы линейно независимы.

Решение задачи 7

Вычислим . Таким образом, данная система векторов образует базис в(см свойство 6 систем векторов из лекции 5). Следовательно,. Найдем коэффициенты, , разложения по этому базису. Для этого перепишем предыдущее равенство в координатной форме

,

откуда получаем систему:

.

Решим эту систему по формулам Крамера:

.

В результате получаем нужное разложение

Решение задачи 8

Используя определения нормы и угла между векторами (см. определение 18 из лекции 6), находим:

; ;

.

Имеем также: . По определению 19 из лекции 7:

.

Решение задачи 9

Согласно определению 20 из лекции 7 векторы иортогональны тогда и только тогда, когда. Имеем:

.

Векторы иколлинеарны (см. задачу 6,б), если координаты этих векторов пропорциональны. Имеем:. Отсюда

.

Решение задачи 10

Площадь равна половине площади параллелограмма, построенного на векторахи. Из теоремы 15 (см. лекцию 8) следует, что площадь параллелограмма равна. По формуле (34) из лекции 8 вычислим векторное произведение:

.

Тогда .

Найдем высоту треугольника, опущенную из вершины(сделать самостоятельно чертеж):

, т.к. .

Решение задачи 11

Применяя теоремы 17 и 16 из лекции 9, имеем:

, где =.

Вычисляем смешанное произведение векторов:

.

Поскольку , то нужно вычислить:

Решение задачи 12

Рассмотрим векторы . Следующие утверждения равносильны:

1. четыре точки лежат в одной плоскости;

2. векторы лежат в одной плоскости, то есть компланарны;

3. объем параллелепипеда, построенного на этих векторах, равен нулю;

4. .

Имеем:

.

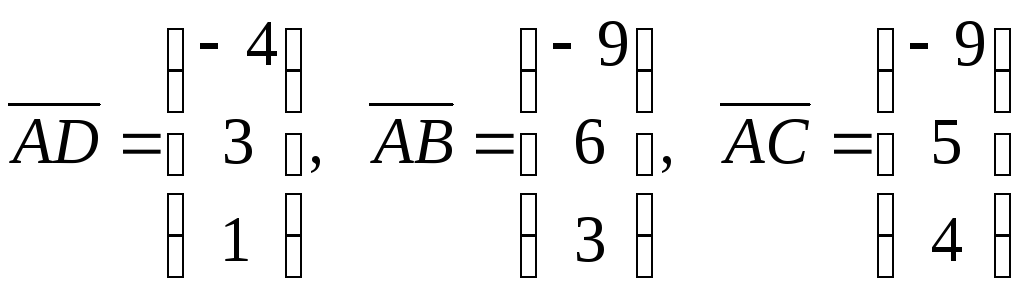Вычисляем: . Таким образом, точкалежит в плоскости.

Вычислим теперь . Здесь .Следовательно, точка не лежит в плоскости.

0