
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
|
|
Утверждено на заседании кафедры высшей математики 11.06.2011 г. |
Линейная алгебра и аналитическая геометрия
Раздел 3. Кривые и поверхности 2-го порядка
Курс лекций
и образец решения индивидуального задания
по высшей математике для бакалавров 1-го курса
очной формы обучения
Ростов-на-Дону
2011
УДК 517(07)
Линейная алгебра и аналитическая геометрия. Раздел 3. Кривые и поверхности 2-го порядка. Курс лекций и образец решения индивидуального задания по высшей математике для бакалавров 1-го курса очной формы обучения. – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 18 с.
Изложен курс лекций по кривым и поверхностям 2-го порядка. Приведен образец индивидуального задания, снабженный подробным решением входящих в него задач.
Предназначены для бакалавров 1-го курса очной формы, проходящих обучение на кафедре высшей математики РГСУ, а также на математических кафедрах других вузов.
Электронная версия находится в библиотеке, ауд. 224.
УДК 517(07)
|
Составитель: |
д-р физ.-мат.наук, проф. И.В. Павлов
|
|
Рецензенты: |
канд. физ.-мат.наук, доц. А.М. Можаев канд. физ.-мат.наук, доц. Г.А. Власков
|
Редактор Т.М. Климчук
Доп. план 2011 г., поз. 178
Подписано в печать 12.07.11. Формат 6084/16. Бумага писчая. Ризограф.
Уч.-изд.л. 1,3. Тираж 50 экз. Заказ 380
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов-на-Дону, ул. Социалистическая, 162
© Ростовский государственный
строительный университет, 2011
Часть 4: кривые и поверхности второго порядка Лекция 13
Кривые второго порядка
Определение
30. Кривой
второго порядка называется кривая,
задающаяся в некоторой прямоугольной
системе координат
![]() уравнением
уравнением
|
|
(53) |
где А, В, С, D, E, F — действительные числа, причём А, В, С одновременно не равны нулю. ٱ
В случае, когда не
существует точек
![]() с действительными координатами,
удовлетворяющих уравнению (53), говорят,
что уравнение (53) определяет мнимую
кривую второго порядка. Примером такого
уравнения может служить уравнение
с действительными координатами,
удовлетворяющих уравнению (53), говорят,
что уравнение (53) определяет мнимую
кривую второго порядка. Примером такого
уравнения может служить уравнение
![]() .
Мы не будем рассматривать ни мнимые
кривые, ни другие «вырожденные» случаи
уравнения (53), как например:
.
Мы не будем рассматривать ни мнимые
кривые, ни другие «вырожденные» случаи
уравнения (53), как например:
а) уравнение пары
пересекающихся прямых:
![]()
![]() ;
;
б) уравнение пары
параллельных или совпадающих прямых:
![]()
![]() ;
;
в) уравнение,
определяющее точку:
![]() .
.
Выделяют три основных нетривиальных случая общего уравнения (53).
1) Уравнение эллипса
|
|
(54) |
с полуосями длины
а
и b.
В частности, при
![]() получаем уравнение окружности
получаем уравнение окружности![]() с центром в начале координат и радиусома.
с центром в начале координат и радиусома.
2) Уравнение гиперболы
|
|
(55) |
с полуосями а и b.
3) Уравнение параболы
|
|
(56) |
Уравнения (54)–(56) называются каноническими. Остановимся подробнее на перечисленных кривых.
Эллипс
Определение
31. Пусть
на плоскости заданы точки
![]() .
Эллипсом с фокусами
.
Эллипсом с фокусами![]() и
и![]() называется геометрическое место точек
называется геометрическое место точек![]() данной плоскости, отличных от точек
данной плоскости, отличных от точек![]() и
и![]() и таких, что сумма расстояний от
и таких, что сумма расстояний от![]() до
до![]() и от
и от![]() до
до![]() постоянна и равна2а.
постоянна и равна2а.
|
|
ٱ |
Имея в виду
определение 31, зададим прямоугольную
систему координат следующим образом.
В качестве оси абсцисс выберем прямую,
проходящую через точки
![]() и
и![]() ;
начало координат
;
начало координат![]() поместим в середину отрезка, соединяющего
поместим в середину отрезка, соединяющего![]() и
и![]() ;
осью
;
осью![]() назначим прямую, проходящую через точку
назначим прямую, проходящую через точку![]() ,
перпендикулярно к оси
,
перпендикулярно к оси![]() .
Ясно, что
.
Ясно, что![]() ,
где
,
где![]() — некоторое число. Тогда точки
— некоторое число. Тогда точки![]() и
и![]() удовлетворяют определению 31 (т.е.
принадлежат эллипсу), причем
удовлетворяют определению 31 (т.е.
принадлежат эллипсу), причем![]() (докажите это!). Обозначим
(докажите это!). Обозначим![]() .
Покажем, что уравнение (54) действительно
является уравнением
.
Покажем, что уравнение (54) действительно
является уравнением
эллипса в смысле определения 31.
Пусть
![]() — произвольная точка эллипса. Имеем:
— произвольная точка эллипса. Имеем:
![]()
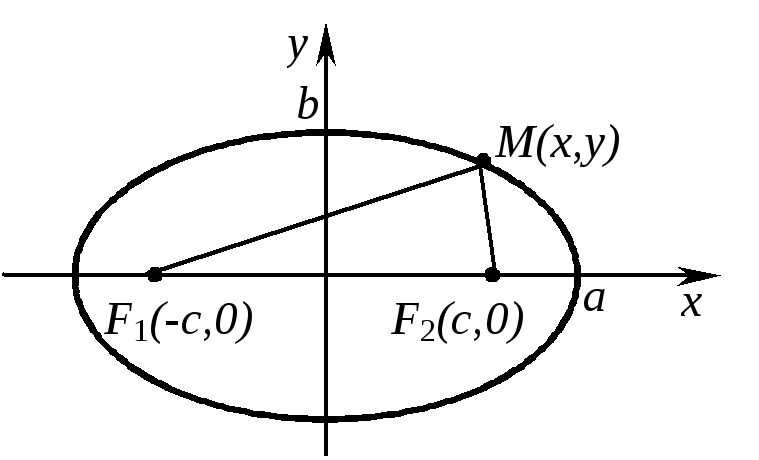 ,
,
![]() .
По определению эллипса должно выполняться
условие
.
По определению эллипса должно выполняться
условие
![]()
![]() .
Проведём выкладки, приводящие это
уравнение к виду (54). Действительно,
.
Проведём выкладки, приводящие это
уравнение к виду (54). Действительно,
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (54).
(54).
Проследив эти
выкладки в обратном порядке, можно
показать, что для произвольной точки
![]() ,
удовлетворяющей уравнению (54), сумма
расстояний от неё до
,
удовлетворяющей уравнению (54), сумма
расстояний от неё до![]() и
и![]() равна
равна![]() (докажите это!).
(докажите это!).
Точки пересечения эллипса с координатными осями называются вершинами эллипса, а отрезки, заключённые между вершинами, называются осями эллипса: большая (фокальная) ось длиной 2а и малая ось длиной 2b. Оси координат являются осями симметрии эллипса, а начало координат — его центром симметрии. Легко понять, что окружность является частным случаем эллипса (фокусы при этом совпадают и служат центром окружности).
Д ля
построения эллипса нарисуем две
концентрические окружности радиусовb
и а
ля
построения эллипса нарисуем две
концентрические окружности радиусовb
и а
![]() с центром в точкеО.
Затем из точки
О проведем
луч под углом
с центром в точкеО.
Затем из точки
О проведем
луч под углом
![]() к осиОх
и обозначим его точки пересечения с
окружностями радиусов b
и а,
соответственно, Т
и N.
Из точки N
проведём прямую, параллельную оси Оу,
а из точки Т
— прямую, параллельную оси Ох.
Точка пересечения М
этих прямых имеет координаты
к осиОх
и обозначим его точки пересечения с
окружностями радиусов b
и а,
соответственно, Т
и N.
Из точки N
проведём прямую, параллельную оси Оу,
а из точки Т
— прямую, параллельную оси Ох.
Точка пересечения М
этих прямых имеет координаты
|
|
(57) |
Так как
 ,
то точка М
принадлежит эллипсу. Легко понять, что
точки, задающиеся уравнениями (57),
покрывают весь эллипс (докажите это!).
,
то точка М
принадлежит эллипсу. Легко понять, что
точки, задающиеся уравнениями (57),
покрывают весь эллипс (докажите это!).
Гипербола
Определение
32. Пусть
на плоскости заданы точки
![]() .
Гиперболой с фокусами
.
Гиперболой с фокусами![]() и
и![]() называется геометрическое место точек
называется геометрическое место точек![]() данной плоскости, отличных от точек
данной плоскости, отличных от точек![]() и
и![]() и таких, что
и таких, что![]() ٱ
ٱ
Введем декартову
систему координат точно так же, как это
делалось при рассмотрении эллипса.
Таким образом,
![]() ,
где
,
где![]() — некоторое число, и точки
— некоторое число, и точки![]() и
и![]() удовлетворяют определению 32 (т.е.
принадлежат гиперболе), причем
удовлетворяют определению 32 (т.е.
принадлежат гиперболе), причем![]() (докажите это!). Обозначим
(докажите это!). Обозначим![]() .
Покажем, что уравнение (55) действительно
является уравнением гиперболы в смысле
определения 32.
.
Покажем, что уравнение (55) действительно
является уравнением гиперболы в смысле
определения 32.
Пусть
![]() — произвольная точка гиперболы. Имеем:
— произвольная точка гиперболы. Имеем:
![]()
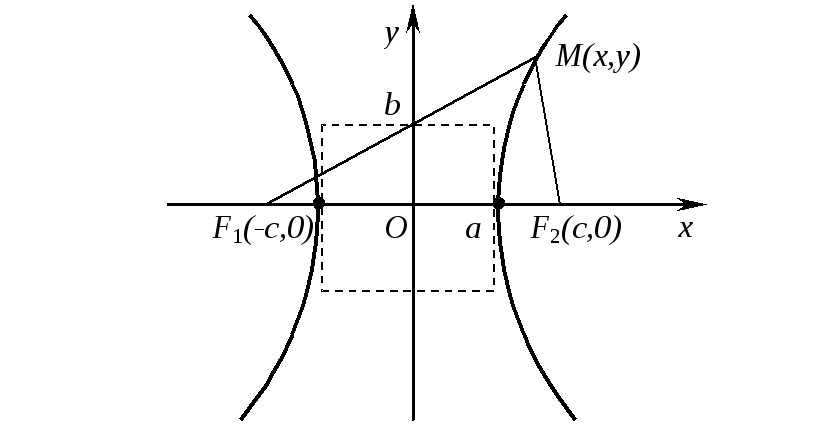 ,
,![]() .
.
Из определения 32 следует:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (55).
(55).
Проследив эти
выкладки в обратном порядке, можно
показать, что для произвольной точки
![]() ,
удовлетворяющей уравнению (55), модуль
разности расстояний от неё до
,
удовлетворяющей уравнению (55), модуль
разности расстояний от неё до![]() и
и![]() равен
равен![]() (докажите это!).
(докажите это!).
Точки пересечения
![]() и
и![]() гиперболы с осьюОх
называются вершинами гиперболы, а
величина а
— действительной полуосью. Точки
гиперболы с осьюОх
называются вершинами гиперболы, а
величина а
— действительной полуосью. Точки
![]() и
и![]() называются мнимыми вершинами гиперболы,
а величинаb
— мнимой полуосью. Прямоугольник с
центром в начале координат и со сторонами,
параллельными координатным осям и
проходящими через вершины параболы,
называется основным прямоугольником
гиперболы. Его диагонали
называются мнимыми вершинами гиперболы,
а величинаb
— мнимой полуосью. Прямоугольник с
центром в начале координат и со сторонами,
параллельными координатным осям и
проходящими через вершины параболы,
называется основным прямоугольником
гиперболы. Его диагонали
![]() являются асимптотами гиперболы. Оси
координат являются осями симметрии
гиперболы, а начало координат — её
центром симметрии. Если
являются асимптотами гиперболы. Оси
координат являются осями симметрии
гиперболы, а начало координат — её
центром симметрии. Если![]() ,
то гипербола называется равносторонней.
,
то гипербола называется равносторонней.
Парабола
Определение
33. Пусть
на плоскости задана прямая
![]() и точка
и точка![]() ,
не лежащая на этой прямой. Параболой
называется геометрическое место точек
,
не лежащая на этой прямой. Параболой
называется геометрическое место точек![]() плоскости, равноудалённых от данной
точки
плоскости, равноудалённых от данной
точки![]() (фокуса) и от данной прямой
(фокуса) и от данной прямой![]() (директрисы).ٱ
(директрисы).ٱ
Если за ось абсцисс принять прямую, проходящую через фокус и перпендикулярную директрисе, а начало координат поместить посередине между фокусом и директрисой, то уравнение параболы примет вид (56).
Д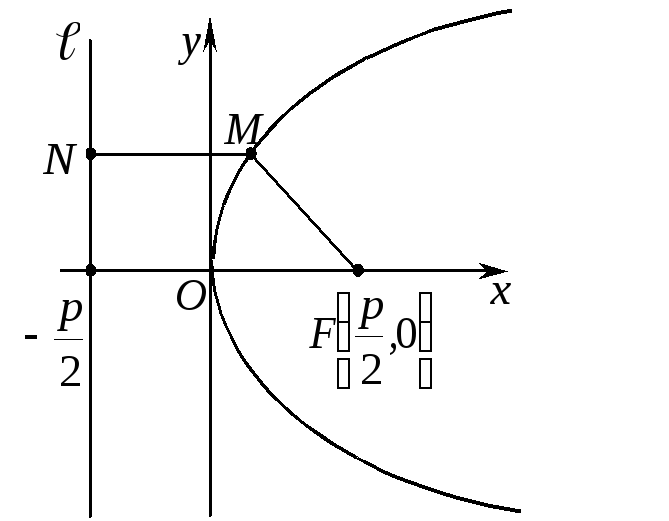 ействительно,
введем
ействительно,
введем![]() такое, что
такое, что![]() ;
обозначим черезN
проекцию точки
;
обозначим черезN
проекцию точки
![]() на директрису. Тогда
на директрису. Тогда
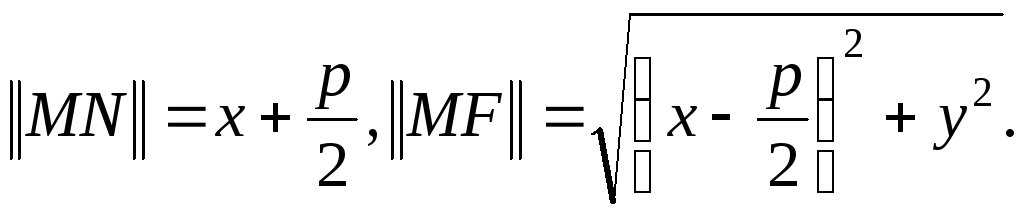 По определению
33:
По определению
33:
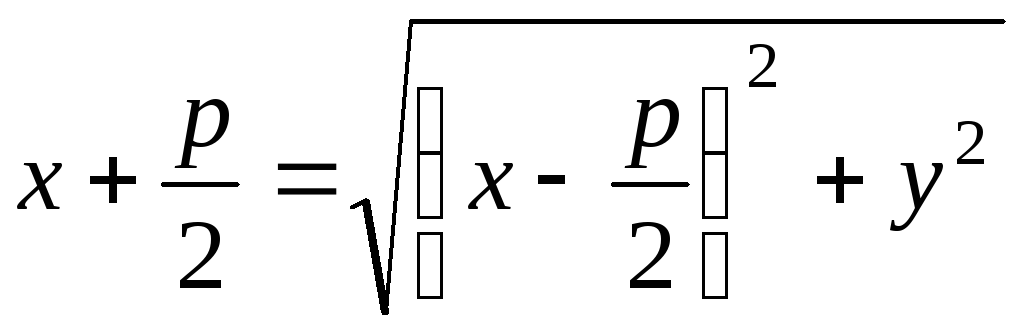
![]()

![]()
![]()
![]() (56).
(56).
Парабола имеет
одну ось симметрии, которая при указанном
выше выборе системы координат совпадает
с осью Ох.
Точка
![]() является вершиной параболы.
является вершиной параболы.
В конкретных
примерах часто встречаются параболы
вида: (а)
![]() ,
(б)
,
(б)![]() и (в)
и (в)![]() .
Представленные уравнения описывают
различные положения параболы в системе
координат, характеризующиеся направлением
ветвей параболы. Так ветви параболы,
заданной уравнением (а) симметричны
относительно осиОх,
но направлены в отрицательную сторону
этой оси. Уравнения (б) и (в) задают
параболы, ветви которых симметричны
относительно оси Oy
и имеют в случае (б) положительное, а в
случае (в) отрицательное направления.
При этом уравнения директрис и координаты
фокусов для каждого представленного
варианта легко находятся. Вершины
парабол во всех перечисленных случаях
совпадают с началом координат.
.
Представленные уравнения описывают
различные положения параболы в системе
координат, характеризующиеся направлением
ветвей параболы. Так ветви параболы,
заданной уравнением (а) симметричны
относительно осиОх,
но направлены в отрицательную сторону
этой оси. Уравнения (б) и (в) задают
параболы, ветви которых симметричны
относительно оси Oy
и имеют в случае (б) положительное, а в
случае (в) отрицательное направления.
При этом уравнения директрис и координаты
фокусов для каждого представленного
варианта легко находятся. Вершины
парабол во всех перечисленных случаях
совпадают с началом координат.

 ,
,